所属成套资源:【同步学案】苏教版(2019)高中数学 选择性必修第一册 同步导学案
活动单导学课程苏教版高中数学选择性必修第一册 1.5.2点到直线的距离(有答案)
展开
这是一份活动单导学课程苏教版高中数学选择性必修第一册 1.5.2点到直线的距离(有答案),共7页。试卷主要包含了 通过公式推导,渗透化归思想., 渗透数形结合的思想.等内容,欢迎下载使用。
1.5.2 点到直线的距离(1)![]() 1. 探索并掌握点到直线的距离公式,会求两平行线间的距离并能运用它们解决一些简单的问题.2. 通过公式推导,渗透化归思想.3. 渗透数形结合的思想.
1. 探索并掌握点到直线的距离公式,会求两平行线间的距离并能运用它们解决一些简单的问题.2. 通过公式推导,渗透化归思想.3. 渗透数形结合的思想.![]()
![]() 活动一探究点到直线距离的求法 问题1:已知点P(2,4)和直线l:5x+4y-7=0,你有几种方法求点P到直线l的距离? 思考1 怎样求点到直线的距离呢? 问题2:已知直线l:Ax+By+C=0(A≠0,B≠0)外一点P(x0,y0),求点P到直线l的距离.
活动一探究点到直线距离的求法 问题1:已知点P(2,4)和直线l:5x+4y-7=0,你有几种方法求点P到直线l的距离? 思考1 怎样求点到直线的距离呢? 问题2:已知直线l:Ax+By+C=0(A≠0,B≠0)外一点P(x0,y0),求点P到直线l的距离. ![]() 点P(x0,y0)到直线l:Ax+By+C=0的距离为d=.
点P(x0,y0)到直线l:Ax+By+C=0的距离为d=.
![]() 活动二通过简单运用加深对点到直线距离公式的理解例1 求点P(-1,2)到下列直线的距离:(1) 2x+y-10=0; (2) y=3x+2;(3) 3x=2; (4) y=-1.
活动二通过简单运用加深对点到直线距离公式的理解例1 求点P(-1,2)到下列直线的距离:(1) 2x+y-10=0; (2) y=3x+2;(3) 3x=2; (4) y=-1. ![]() 1. 用点到直线的距离公式时,直线方程必须是一般式.2. 当A=0或B=0时,此公式也同样成立,但我们一般不用此公式,直接画图利用图形性质求解.
1. 用点到直线的距离公式时,直线方程必须是一般式.2. 当A=0或B=0时,此公式也同样成立,但我们一般不用此公式,直接画图利用图形性质求解.![]() 求过点P(-1,2),且与原点的距离等于的直线方程.
求过点P(-1,2),且与原点的距离等于的直线方程. ![]() 本题设直线方程时一定要先考虑直线的斜率是否存在,体现数学思维的严密性与分类的思想.
本题设直线方程时一定要先考虑直线的斜率是否存在,体现数学思维的严密性与分类的思想. ![]() 活动三探究两条平行直线间的距离 例2 求两条平行直线x+3y-4=0和2x+6y-9=0之间的距离. 思考2 如何求两条平行直线之间的距离? 探究:任意两条平行直线Ax+By+C1=0与Ax+By+C2=0(C1≠C2)间的距离如何表示? 结论:对于任意两条平行直线l1:Ax+By+C1=0,l2:Ax+By+C2=0(C1≠C2),它们之间的距离为d=.(两条平行直线之间的距离公式的使用注意点:只有两条直线方程中x,y前面的系数相同时才能使用上面的公式)
活动三探究两条平行直线间的距离 例2 求两条平行直线x+3y-4=0和2x+6y-9=0之间的距离. 思考2 如何求两条平行直线之间的距离? 探究:任意两条平行直线Ax+By+C1=0与Ax+By+C2=0(C1≠C2)间的距离如何表示? 结论:对于任意两条平行直线l1:Ax+By+C1=0,l2:Ax+By+C2=0(C1≠C2),它们之间的距离为d=.(两条平行直线之间的距离公式的使用注意点:只有两条直线方程中x,y前面的系数相同时才能使用上面的公式)![]() 若直线l1与直线l2:3x-4y-20=0平行且距离为3,求直线l1的方程. 思考3 由直线l1与l2平行,如何设直线l1的方程能简化运算?
若直线l1与直线l2:3x-4y-20=0平行且距离为3,求直线l1的方程. 思考3 由直线l1与l2平行,如何设直线l1的方程能简化运算? ![]() 1. 已知△ABC的三个顶点坐标分别为A(2,6),B(-4,3),C(2,-3),则点A到边BC的距离为 ( )A. B. C. D. 42. 两条直线y=x,6x-4y+13=0之间的距离为( )A. B. C. D. 133. (多选)已知直线l过点P(3,4)且与点A(-2,2),B(4,-2)等距离,则直线l的方程可以是( )A. 2x+3y-18=0 B. 2x-y-2=0C. 3x-2y+18=0 D. 2x-y+2=04. 若点P在直线3x+y-5=0上,且点P到直线x-y-1=0的距离为,则点P的坐标为____________.5. 求经过点A(-1,-2),且到原点的距离为1的直线方程. 参考答案与解析【活动方案】问题1: 如图,过点P作PE⊥l,垂足为E,则点P到直线l的距离就是线段PE的长.方法一:通过求点E的坐标,用两点间距离公式求PE.由PE⊥l,可知PE所在直线的斜率为,所以PE所在直线的方程为y-4=(x-2),即4x-5y+12=0.联立方程组解得垂足E的坐标为.由两点间距离公式,得点P到直线l的距离PE==.方法二:通过构造三角形,利用面积关系求点P到直线l的距离.如图,过点P分别作y轴、x轴的垂线,交直线l于点M,N,则M,N,则PM=|--2|=,PN=|--4|=.由勾股定理,得MN===.由三角形面积公式可知PE===.
1. 已知△ABC的三个顶点坐标分别为A(2,6),B(-4,3),C(2,-3),则点A到边BC的距离为 ( )A. B. C. D. 42. 两条直线y=x,6x-4y+13=0之间的距离为( )A. B. C. D. 133. (多选)已知直线l过点P(3,4)且与点A(-2,2),B(4,-2)等距离,则直线l的方程可以是( )A. 2x+3y-18=0 B. 2x-y-2=0C. 3x-2y+18=0 D. 2x-y+2=04. 若点P在直线3x+y-5=0上,且点P到直线x-y-1=0的距离为,则点P的坐标为____________.5. 求经过点A(-1,-2),且到原点的距离为1的直线方程. 参考答案与解析【活动方案】问题1: 如图,过点P作PE⊥l,垂足为E,则点P到直线l的距离就是线段PE的长.方法一:通过求点E的坐标,用两点间距离公式求PE.由PE⊥l,可知PE所在直线的斜率为,所以PE所在直线的方程为y-4=(x-2),即4x-5y+12=0.联立方程组解得垂足E的坐标为.由两点间距离公式,得点P到直线l的距离PE==.方法二:通过构造三角形,利用面积关系求点P到直线l的距离.如图,过点P分别作y轴、x轴的垂线,交直线l于点M,N,则M,N,则PM=|--2|=,PN=|--4|=.由勾股定理,得MN===.由三角形面积公式可知PE===. 思考1:运用数形结合的思想,将求点到直线的距离转化为求水平或垂直线段的长度,进而通过面积关系加以解决.问题2:如图,过点P作PQ⊥l,垂足为Q.过点P分别作y轴、x轴的平行线,交l于点M(x1,y0),N(x0,y2). 由Ax1+By0+C=0,Ax0+By2+C=0,得x1=,y2=,所以PM=|x1-x0|=,PN=|y2-y0|=.因为PQ是Rt△PMN斜边上的高,所以由直角三角形面积公式可知PQ===,即点P到直线l的距离为.
思考1:运用数形结合的思想,将求点到直线的距离转化为求水平或垂直线段的长度,进而通过面积关系加以解决.问题2:如图,过点P作PQ⊥l,垂足为Q.过点P分别作y轴、x轴的平行线,交l于点M(x1,y0),N(x0,y2). 由Ax1+By0+C=0,Ax0+By2+C=0,得x1=,y2=,所以PM=|x1-x0|=,PN=|y2-y0|=.因为PQ是Rt△PMN斜边上的高,所以由直角三角形面积公式可知PQ===,即点P到直线l的距离为.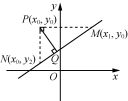 例1 (1) d===2.(2) y=3x+2化为一般式为3x-y+2=0,则d==.(3) 因为直线3x=2平行于y轴,所以d==.(4) d==3.跟踪训练 当直线斜率不存在时,直线方程为x=-1,不符合题意;当直线斜率存在时,设直线方程为y-2=k(x+1),即kx-y+k+2=0.由题意,得=,解得k=-1或k=-7,所以所求的直线方程为x+y-1=0或7x+y+5=0.例2 在直线x+3y-4=0上取点P(4,0),则点P(4,0)到直线2x+6y-9=0的距离d就是两条平行直线之间的距离,所以d===. 思考2:只要在其中一条直线上任意取一个点,求出该点到另一条直线的距离即可,从而将两条平行直线之间的距离转化为点到直线的距离.探究:d=跟踪训练 设所求直线方程为3x-4y+m=0,由题意,得=3,解得m=-5或m=-35,所以所求的直线方程为3x-4y-5=0或3x-4y-35=0.思考3:设直线l1的方程时,直线l1方程中x,y的系数与直线l2方程中x,y的系数相同.【检测反馈】1. B 解析:边BC所在直线的方程为=,即x+y+1=0,则d==.2. B 解析:两条直线的方程分别为3x-2y=0,3x-2y+=0,所以两条直线之间的距离d==.3. AB 解析:若直线l的斜率不存在,则直线l:x=3,不符合题意,故直线l的斜率存在.设所求直线的方程为y-4=k(x-3),即kx-y-3k+4=0,由已知及点到直线的距离公式,得=,解得k=2或k=-,即所求直线方程为2x+3y-18=0或2x-y-2=0.故选AB.4. (1,2)或(2,—1) 解析:由于点P在直线3x+y-5=0上,故设点P(a,5-3a).又点P到直线x-y-1=0的距离为,所以=,即|4a-6|=2,解得a=1或a=2,故点P的坐标为(1,2)或(2,-1).5. 当过点A(-1,-2)的直线的斜率不存在,即垂直于x轴时,它到原点的距离为1,满足题意,其方程为x=-1.当过点A的直线的斜率存在时,设所求的直线方程为y+2=k(x+1),即kx-y+k-2=0.因为原点到该直线的距离等于1,所以=1,解得k=.故所求的直线方程为y+2=(x+1),即3x-4y-5=0.综上所述,所求直线的方程为x=-1或3x-4y-5=0.
例1 (1) d===2.(2) y=3x+2化为一般式为3x-y+2=0,则d==.(3) 因为直线3x=2平行于y轴,所以d==.(4) d==3.跟踪训练 当直线斜率不存在时,直线方程为x=-1,不符合题意;当直线斜率存在时,设直线方程为y-2=k(x+1),即kx-y+k+2=0.由题意,得=,解得k=-1或k=-7,所以所求的直线方程为x+y-1=0或7x+y+5=0.例2 在直线x+3y-4=0上取点P(4,0),则点P(4,0)到直线2x+6y-9=0的距离d就是两条平行直线之间的距离,所以d===. 思考2:只要在其中一条直线上任意取一个点,求出该点到另一条直线的距离即可,从而将两条平行直线之间的距离转化为点到直线的距离.探究:d=跟踪训练 设所求直线方程为3x-4y+m=0,由题意,得=3,解得m=-5或m=-35,所以所求的直线方程为3x-4y-5=0或3x-4y-35=0.思考3:设直线l1的方程时,直线l1方程中x,y的系数与直线l2方程中x,y的系数相同.【检测反馈】1. B 解析:边BC所在直线的方程为=,即x+y+1=0,则d==.2. B 解析:两条直线的方程分别为3x-2y=0,3x-2y+=0,所以两条直线之间的距离d==.3. AB 解析:若直线l的斜率不存在,则直线l:x=3,不符合题意,故直线l的斜率存在.设所求直线的方程为y-4=k(x-3),即kx-y-3k+4=0,由已知及点到直线的距离公式,得=,解得k=2或k=-,即所求直线方程为2x+3y-18=0或2x-y-2=0.故选AB.4. (1,2)或(2,—1) 解析:由于点P在直线3x+y-5=0上,故设点P(a,5-3a).又点P到直线x-y-1=0的距离为,所以=,即|4a-6|=2,解得a=1或a=2,故点P的坐标为(1,2)或(2,-1).5. 当过点A(-1,-2)的直线的斜率不存在,即垂直于x轴时,它到原点的距离为1,满足题意,其方程为x=-1.当过点A的直线的斜率存在时,设所求的直线方程为y+2=k(x+1),即kx-y+k-2=0.因为原点到该直线的距离等于1,所以=1,解得k=.故所求的直线方程为y+2=(x+1),即3x-4y-5=0.综上所述,所求直线的方程为x=-1或3x-4y-5=0.
相关试卷
这是一份苏教版 高中数学 选择性必修第一册 活动单导学课程 1.2.3直线的一般式方程(有答案),共5页。试卷主要包含了 下列说法中,正确的是等内容,欢迎下载使用。
这是一份苏教版 高中数学 选择性必修第一册 活动单导学课程 1.2.2 直线的两点式方程(有答案),共7页。试卷主要包含了 下列说法中,错误的是, 已知直线l经过点和点.等内容,欢迎下载使用。
这是一份苏教版 高中数学 选择性必修第一册 活动单导学课程 1.2.1直线的点斜式方程(有答案),共5页。试卷主要包含了2.1 直线的点斜式方程等内容,欢迎下载使用。