活动单导学课程苏教版高中数学选择性必修第一册1.3.2两条直线的平行与垂直（有答案）

这是一份活动单导学课程苏教版高中数学选择性必修第一册1.3.2两条直线的平行与垂直（有答案），共6页。试卷主要包含了 若直线l等内容，欢迎下载使用。
1．3.2　两条直线的平行与垂直(2)1. 掌握用斜率判断两条直线垂直的方法，感受用代数方法研究几何图形性质的思想．2. 应用两直线垂直的相关知识求直线方程． 活动一探究两条直线垂直的条件1. 知识回顾如何判断两条直线是否平行？  2. 探究两条直线垂直的条件(1) 若两条直线垂直，它们的倾斜角之间有怎样的关系？  (2) 能否用斜率刻画两条直线的垂直关系？  (3) 设直线l1，l2的斜率分别为k1，k2，若l1⊥l2，则斜率k1，k2满足什么关系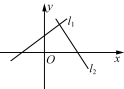？ 结论：对于两条不重合的直线l1，l2，其斜率为k1，k2，有l1⊥l2k1k2＝－1.思考1 对任意的两条直线l1，l2，“l1⊥l2”的充要条件是“k1k2＝－1”吗？   思考2 对直线的斜率不存在的情况，如何判断两直线是否垂直？   例1　(1) 已知四点A(5，3)，B(10，6)，C(3，－4)，D(－6，11)，求证：AB⊥CD；(2) 已知直线l1的斜率为k1＝，直线l2经过点A(3a，－2)，B(0，a2＋1)，且l1⊥l2，求实数a的值．    活动二判断两直线垂直　例2　(1) 已知△ABC的顶点A(1，3)，B(2，7)，C(－3，4)，判断△ABC的形状；(2) 已知直线l1：3x＋5y－10＝0，l2：15x－9y＋8＝0，求证：l1⊥l2.     若k1k2＝－1，则两条直线垂直，使用它的前提条件是两条直线斜率都存在．若其中一条直线的斜率不存在，另一条直线的斜率为零，此时两直线也垂直． 　已知定点A(－1，3)，B(4，2)，以AB为直径作圆，与x轴有交点P，则交点P的坐标是__________.     活动三求直线方程例3　已知三角形的三个顶点为A(2，4)，B(1，－2)，C(－2，3)，求BC边上的高AD所在的直线方程．     与直线Ax＋By＋C＝0垂直的直线的方程可设为Bx－Ay＋m＝0，其中m待定．　过点A(2，3)，且垂直于直线x－y－2＝0的直线的方程为________________________________________________________________.例4　在路边安装路灯，路宽23 m，灯杆长2.5 m，且与灯柱成120°角．路灯采用锥形灯罩，灯罩轴线与灯杆垂直．当灯柱高为多少米时，灯罩轴线正好通过道路路面的中线(精确到0.01 m)?    
1. 已知两条直线y＝ax－2和y＝(a＋2)x＋1互相垂直，则a的值为(　　) A. －1  B. 2  C. 1  D. 32. 已知△ABC的顶点B(2，1)，C(－6，3)，其垂心为H(－3，2)，则其顶点A的坐标为(　　)A. (－19，－62)  B. (19，－62)  C. (－19，62)  D. (19，62)3. (多选)设点P(－4，2)，Q(6，－4)，R(12，6)，S(2，12)，给出下面四个结论，其中正确的是(　　)A. PQ∥SR  B. PQ⊥PS  C. PS∥QS  D.  RP⊥QS4. 若直线l：x＋2y＋5＝0绕点A(1，－3)逆时针旋转90°得到直线m，则直线m与两坐标轴围成的三角形的面积为________．5. 已知在平行四边形ABCD中，点A(1，2)，B(5，0)，C(3，4)．(1) 求点D的坐标；(2) 试判断平行四边形ABCD是否为菱形．      参考答案与解析【活动方案】1. l1∥l2k1＝k2(k1，k2均存在)，这里l1，l2指不重合的两条直线．2. (1) 两条直线的倾斜角之差为.(2) 能(3) k1·k2＝－1.思考1：不是．若有一条直线的斜率不存在，则l1⊥l2k1k2＝－1不正确．思考2：两条直线中，若一条直线的斜率不存在，则当另一条直线的斜率为0时，两直线垂直．例1　(1) 由斜率公式，得kAB＝，kCD＝－，所以kAB·kCD＝－1，所以AB⊥CD.(2) 因为l1⊥l2，所以k1·k2＝－1，即×＝－1，解得a＝1或a＝3.例2　(1) 因为点A(1，3)，B(2，7)，C(－3，4)，所以kAB＝＝4，kAC＝＝－，kBC＝＝.设F为BC的中点，则F，kAF＝＝－.因为kA B·kA C＝－1，kBC·kA F＝－1，所以△ABC是等腰直角三角形．(2) 由l1，l2的方程可知，它们的斜率k1＝－，k2＝＝，从而k1k2＝×＝－1，所以l1⊥l2.跟踪训练　(1，0)或(2，0)　解析：设以AB为直径的圆与x轴的交点为P(x，0)．因为kPB≠0，kPA≠0，所以kPA·kPB＝－1，即·＝－1，所以(x＋1)(x－4)＝－6，即x2－3x＋2＝0，解得x＝1或x＝2.故点P的坐标为(1，0)或(2，0)．例3　直线BC的斜率kBC＝＝－.因为AD⊥BC，所以kAD＝.根据直线的点斜式方程，得所求直线的方程为y－4＝(x－2)，即3x－5y＋14＝0.跟踪训练　x＋y－5＝0　解析：设所求直线的方程为x＋y＋a＝0，将点A(2，3)代入，得2＋3＋a＝0，解得a＝－5，故所求直线的方程为x＋y－5＝0.例4　如图，记灯柱顶端为B，灯罩顶为A，灯杆为AB.灯罩轴线与道路中线交于点C，灯柱的高为h m．以灯柱底端点O为原点，灯柱OB所在直线为y轴，建立如图所示的直角坐标系．点B的坐标为(0，h)，点C的坐标为(11.5，0)．因为∠OBA＝120°，所以直线BA的倾斜角为30° ，从而点A的坐标为(2.5cos30°，h＋2.5sin30°)，即(1.25，h＋1.25)．因为CA⊥BA，所以kCA＝－＝－＝－，从而直线CA的方程是y－(h＋1.25)＝－(x－1.25)．又灯罩轴线CA过点C(11.5，0)，则－(h＋1.25)＝－(11.5－1.25)，解得h≈14.92.故当灯柱高约为 14.92 m时，灯罩轴线正好通过道路路面的中线．【检测反馈】1. A　解析：由题意，得a(a＋2)＝－1，解得a＝－1.2. A　解析：因为H为△ABC的垂心，所以AH⊥BC，BH⊥AC.又kBC＝＝－，kBH＝＝－，所以直线AH，AC的斜率存在且kAH＝4，kAC＝5.设点A的坐标为(x，y)，则解得所以点A(－19，－62)．3. ABD　解析：因为kPQ＝＝－，kSR＝＝－，kPS＝＝，kQS＝＝－4，kPR＝＝.又P，Q，S，R四点不共线，根据直线位置关系的判断可得PQ∥SR，PS⊥PQ，RP⊥QS.故选ABD.4. 　解析：由直线l：x＋2y＋5＝0绕点A(1，－3)逆时针旋转90°得到直线m，可得m⊥l，所以km·kl＝km×＝－1，解得km＝2.又直线m过点A(1，－3)，则由直线的点斜式方程，可得直线m的方程为y－(－3)＝2(x－1)，即2x－y－5＝0，所以所求三角形的面积为××5＝.5. (1) 设D(a，b)，因为四边形ABCD为平行四边形，所以kAB＝kCD，kAD＝kBC，所以解得所以点D(－1，6)．(2) 因为kAC＝＝1，kBD＝＝－1，所以kAC·kBD＝－1，所以AC⊥BD，所以ABCD为菱形．