苏教版 高中数学 选择性必修第一册 活动单导学课程 第1章 直线与方程复习（有答案）

这是一份苏教版 高中数学 选择性必修第一册 活动单导学课程 第1章 直线与方程复习（有答案），共8页。试卷主要包含了 梳理本章知识，构建知识网络．， 下列说法中，正确的是， 已知点P，直线l等内容，欢迎下载使用。
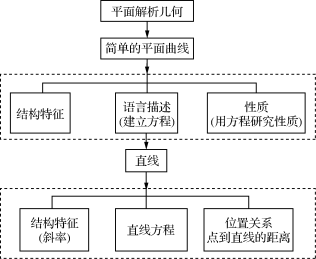本 章 复 习1. 梳理本章知识，构建知识网络．2. 巩固直线的有关知识与思想方法． 活动一建构知识网络　　1. 知识结构框图2. 直线中的相关知识(1) 直线的倾斜角α和斜率k①直线倾斜角的范围为________；②直线的斜率k＝________；③过两点P1(x1，y1)，P1(x2，y2)(x1≠x2)的直线的斜率k＝________；④不重合且斜率存在的两条直线l1，l2. l1∥l2⇔________；l1⊥l2⇔________． (2) 直线的方程①点斜式方程为______________；②斜截式方程为______________；③两点式方程为______________；④截距式方程为______________；⑤一般式方程为______________．(3) 距离公式①两点P1(x1，y1)，P2(x2，y2)间的距离公式为________________________；②点P0(x0，y0)到直线l：Ax＋By＋C＝0的距离为________________________；③两条平行直线Ax＋By＋C1＝0与Ax＋By＋C2＝0间的距离为________________．(4) 两条直线l1：A1x＋B1y＋C1＝0与l2：A2x＋B2y＋C2＝0的位置关系①l1与l2相交⇔________________；②l1∥l2⇔________________________；③l1⊥l2⇔________________．(5) 三种常见的对称问题①点关于点的对称点P(x0，y0)关于点M(a，b)的对称点为P′________；　②点关于直线的对称若两点P1(x1，y1)与P2(x2，y2)关于直线l：Ax＋By＋C＝0对称，则由方程组可得点P1关于l对称的点P2的坐标(x2，y2)(其中A≠0，x1≠x2)；③线关于点、线的对称线是点构成的集合，直线的方程是直线上任一点P(x，y)的坐标x，y满足的表达式，故求直线关于点、线的对称，可转化为求该直线上任一点关于点、线的对称．  活动二直线的方程例1　在平面直角坐标系中，已知菱形ABCD的顶点A(－1，2)和C(5，4)，AB所在直线的方程为x－y＋3＝0.(1)  求对角线BD所在直线的方程；(2)  求AD所在直线的方程．       例2　已知直线l经过点P(－2，3)．(1) 若原点到直线l的距离为2，求直线l的方程；(2) 若直线l被两条相交直线l1：2x－y－2＝0和l2：x＋y＋3＝0所截得的线段恰被点P平分，求直线l的方程．        活动三两直线的位置关系例3　已知l1：3x＋2ay－5＝0，l2：(3a－1)x－ay－2＝0，求使l1∥l2的a的值．   例4　已知△ABC的三个顶点A(4，－6)，B(－4，0)，C(－1，4)，求：(1) AC边上的高BD所在直线的方程；(2) BC的垂直平分线EF所在直线的方程．     活动四直线的综合应用例5　求直线a：2x＋y－4＝0关于直线l：3x＋4y－1＝0对称的直线b的方程．  例6　设直线l的方程为(2－m)x＋(2m＋1)y＋3m＋4＝0.(1) 当m为何值时，点Q(3，4)到直线l的距离最大，最大值为多少？(2) 若直线l分别与x轴，y轴的负半轴交于A，B两点，求三角形AOB面积的最小值及此时直线l的方程．
1. 已知点M(1，4)到直线l：mx＋y－1＝0的距离等于1，则实数m的值为(　　)A.   B. －  C. －  D. 2. 如果直线l1的斜率为a，l1⊥l2，那么直线l2的斜率为(　　)A.   B. a  C. －  D. －或不存在3. (多选)下列说法中，正确的是(　　)A. 过(x1，y1)，(x2，y2)两点的直线方程为＝B. 点(0，2)关于直线y＝x＋1的对称点为(1，1)C. 直线x－y－2＝0与两坐标轴围成的三角形的面积是2D. 经过点(1，1)且在x轴和y轴上截距都相等的直线方程为x＋y－2＝04. 已知点P(－2，2)，直线l：(λ＋2)x－(λ＋1)y－4λ－6＝0，则点P到直线l的距离的取值范围为________．5. 已知正方形ABCD的边CD所在直线的方程为x＋3y－13＝0，对角线AC，BD的交点为P(1，5)，求正方形ABCD其他三边所在直线的方程．
参考答案与解析【活动方案】活动一　略例1　(1) 由A(－1，2)和C(5，4)，得kAC＝＝，AC的中点M(2，3)．因为四边形ABCD为菱形，所以BD⊥AC，且M(2，3)为BD的中点，所以kBD＝－3，所以对角线BD所在直线的方程为y－3＝－3(x－2)，即3x＋y－9＝0.(2) 由解得点B，所以kBC＝＝－.因为AD∥BC，所以kAD＝－，所以直线AD的方程为y－2＝－(x＋1)，即x＋7y－13＝0.例2　(1) ①当直线l的斜率不存在时，显然成立，直线方程为x＝－2.②当直线斜率存在时，设直线l的方程为y－3＝k(x＋2)，即kx－y＋2k＋3＝0.由原点到直线l的距离为2，得＝2，解得k＝－，故直线l的方程为y－3＝－(x＋2)，即y＝－x＋.综上，所求直线的方程为x＝－2或y＝－x＋.(2) 设直线l夹在直线l1，l2之间的线段为AB(点A在l1上，点B在l2上)，A，B的坐标分别设为(x1，y1)，(x2，y2)．因为AB被点P平分，所以x1＋x2＝－4，y1＋y2＝6，于是x2＝－4－x1，y2＝6－y1.由于点A在l1上，点B在l2上，即则解得x1＝，y1＝，即点A的坐标是，故直线l的方程是＝，即y＝－＋.例3　当直线斜率不存在，即a＝0时，有l1：3x－5＝0，l2：－x－2＝0，符合l1∥l2；当直线斜率存在时，若l1∥l2，则－＝，解得a＝－.故使l1∥l2的a的值为0或－.例4　(1) 由斜率公式易知kAC＝－2，所以直线BD的斜率k＝.又直线BD过点B(－4，0)，代入点斜式，得直线BD的方程为x－2y＋4＝0.(2) 因为kBC＝，所以kEF＝－.又线段BC的中点为，所以EF所在直线的方程为y－2＝－.整理，得所求的直线方程为6x＋8y－1＝0.例5　在直线a：2x＋y－4＝0上取一点A(2，0)，设点A关于直线l的对称点B(x0，y0)，则解得点B.由解得交点D(3，－2)．由两点式方程得直线b的方程为2x＋11y＋16＝0.例6　(1) 根据题意，得直线l过定点P(－1，－2)，则由点Q(3，4)到直线的距离最大，可知点Q与定点P(－1，－2)的连线的距离就是所求最大值，即＝2为最大值．因为kPQ＝＝，所以直线(2－m)x＋(2m＋1)y＋3m＋4＝0的斜率为－，即－＝－，解得m＝.(2) 若直线分别与x轴，y轴的负半轴交于A，B两点，直线l方程为y＋2＝k(x＋1)，k<0，则点A，B(0，k－2)，S△AOB＝|－1|·|k－2|＝(k－2)＝2＋≥2＋2＝4，当且仅当k＝－2时取等号，所以面积的最小值为4，此时直线的方程为2x＋y＋4＝0.【检测反馈】1. C　解析：由题意，得＝1，解得m＝－.2. D　解析：当a≠0时，由l1⊥l2，得kl1·kl2＝a·kl2＝－1，所以kl2＝－；当a＝0时，直线l1与x轴平行或重合，则直线l2与y轴平行或重合，直线l2的斜率不存在．综上，直线l2的斜率为－或不存在．3. BC　解析：对于A，当x1≠x2，y1≠y2时，过(x1，y1)，(x2，y2)两点的直线方程为＝，故A错误；对于B，点(0，2)与 (1，1) 的中点坐标为，满足直线方程y＝x＋1，并且过点(0，2)与(1，1)的直线的斜率为－1，所以点(0，2)关于直线 y＝x＋1 的对称点为 (1，1)，故B正确；对于C，直线x－y－2＝0在两坐标轴上的截距分别为2，－2，直线x－y－2＝0与坐标轴围成的三角形的面积是×2×2＝2，故C正确；对于D，经过点(1，1) 且在 x 轴和 y 轴上截距都相等的直线方程为 x＋y－2＝0 或 y＝x，故D错误．故选BC.4. [0，4)　解析：将直线l：(λ＋2)x－(λ＋1)y－4λ－6＝0化为(2x－y－6)＋λ(x－y－4)＝0，联立方程组解得即直线l过定点M(2，－2)．又由kPM＝＝－1，且·(－1)≠－1，所以直线PM与l不垂直，所以点P到直线l的距离d满足0≤d<PM＝＝4，即点P到直线l的距离的取值范围为[0，4)．5. 设点P(1，5)到直线CD的距离为d，则d＝.因为直线AB平行于直线CD，所以可设直线AB的方程为x＋3y＋m＝0(m≠－13)．点P(1，5)到直线AB的距离也等于d，则＝.又因为m≠－13，所以m＝－19，即直线AB的方程为x＋3y－19＝0.因为直线AD垂直于直线CD，所以可设直线AD的方程为3x－y＋n＝0，点P(1，5)到直线AD的距离也等于d，则＝，解得n＝5或n＝－1.结合图形(图略)知直线AD的方程为3x－y＋5＝0，直线BC的方程为3x－y－1＝0，所以正方形ABCD其他三边所在直线的方程为x＋3y－19＝0，3x－y＋5＝0，3x－y－1＝0.