苏教版 高中数学 选择性必修第一册 活动单导学课程 1.2.3直线的一般式方程（有答案）

这是一份苏教版 高中数学 选择性必修第一册 活动单导学课程 1.2.3直线的一般式方程（有答案），共5页。试卷主要包含了 下列说法中，正确的是等内容，欢迎下载使用。
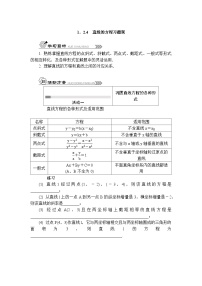
1．2.3　直线的一般式方程1. 掌握直线的一般式方程Ax＋By＋C＝0(A，B不全为0)，能正确理解直线的一般式方程的含义．2. 了解直线的一般式方程与二元一次方程之间的对应关系． 活动一直线的一般式方程的推导　　回顾直线的点斜式、斜截式、两点式、截距式方程： 思考1 (1) 这些方程分别适用于哪些情形？ (2) 这些方程有什么共同的特点？ (3) 平面直角坐标系中的每一条直线都可以用一个关于x，y的二元一次方程表示吗？ (4) 每一个关于x，y的二元一次方程Ax＋By＋C＝0(A，B不全为0)都表示一条直线吗？结论：我们把关于x，y的二元一次方程Ax＋By＋C＝0(A，B不全为0)叫作直线的一般式方程．思考2 直线方程的一般式与其他几种形式的直线方程相比，它有什么优点？  活动二求直线的方程 例1　已知直线经过点A(6，－4)，且斜率为－，求直线的点斜式方程和一般式方程． 例2　求直线l：3x＋5y－15＝0的斜率以及它在x轴、y轴上的截距，并作图．  例3　已知直线l经过点A(2，4)，斜率为－，求直线l的点斜式方程、一般式方程、斜截式方程和截距式方程．   活动三直线的一般式方程的应用例4　设直线l的方程为x＋my－2m＋6＝0(m∈R)，根据下列条件分别确定m的值．(1) 直线l在x轴上的截距是－3；(2) 直线l的斜率是1.    例5　直线方程Ax＋By＋C＝0(A，B不全为0)的系数A，B，C分别满足什么关系时，这条直线有以下性质？(1) 与两条坐标轴都相交；(2) 只与x轴相交；(3) 只与y轴相交；(4) 是x轴所在直线；(5) 是y轴所在直线．       
1. 已知直线l过点(－2，1)，且倾斜角是，则直线l的方程是(　　)A. x＋y＋1＝0  B. y＝－xC. x＋2＝0  D. y－1＝02. 已知直线(m2－2m－3)x＋(2m2＋m－1)y－2m＋6＝0的斜率为1，则m的值为(　　)A. －  B. －   C. 2    D. 3. (多选)下列说法中，正确的是(　　)A. 直线y＝ax－3a＋2(a∈R)必过定点(3，2)B. 直线y＝3x－2在y轴上的截距为－2C. 直线x＋y＋1＝0的倾斜角为60°D. 经过点(1，1)且在x轴和y轴上的截距都相等的直线方程为x＋y－2＝0或x－y＝04. 若直线x－y＋2m＝0与两坐标轴围成的三角形的面积不小于8，则实数m的取值范围为________________．5. 根据下列各条件写出直线的方程，并化成一般式方程．(1) 斜率是－，经过点A(8，－2); (2) 经过点B(4，2)，平行于x轴；(3) 在x轴和y轴上的截距分别是，－3；(4) 经过两点P1(3，－2)，P2(5，－4).             参考答与解析【活动方案】点斜式：y－y1＝k(x－x1)；斜截式：y＝kx＋b；两点式：＝；截距式：＋＝1.思考1：(1) 点斜式适用于不含直线x＝x1的直线；斜截式适用于不含垂直于x轴的直线；两点式适用于不含与x轴或y轴垂直的直线；截距式适用于不含垂直于坐标轴和过原点的直线．(2) 共同特点：都是关于x和y的二元一次方程．(3) 可以．(4) 当B≠0时，方程Ax＋By＋C＝0可以写成y＝－x－，它表示斜率为－，在y轴上的截距为－的直线；当A＝0，B≠0时，它表示垂直于y轴的直线；当B＝0，A≠0时，它表示垂直于x轴的直线．因此，在平面直角坐标系中，任何一个关于x，y的二元一次方程Ax＋By＋C＝0(A，B不全为0)都表示一条直线．思考2：优点：其他几种形式的直线方程都有适用范围，而直线的一般式方程对于平面直角坐标系中的直线都适用．例1　由题意知直线的点斜式方程为y＋4＝－(x－6)，直线的一般式方程为4x＋3y－12＝0.例2　直线l的方程可写成y＝－x＋3，所以直线l的斜率k＝－，则直线l在y轴上的截距为3，在x轴上的截距为5.作图略．例3　点斜式：y－4＝－(x－2)；一般式：2x＋3y－16＝0；斜截式：y＝－x＋；截距式：＋＝1.例4　(1) 由题意知直线l过点(－3，0)，所以－3＋0－2m＋6＝0，解得m＝.(2) 由题意知－＝1，解得m＝－1.例5　(1) 当A≠0，B≠0时，直线与两条坐标轴都相交. (2) 当A≠0，B＝0，C≠0时，直线只与x轴相交．(3) 当A＝0，B≠0，C≠0时，直线只与y轴相交. (4) 当A＝0，B≠0，C＝0时，直线是x轴所在直线．(5) 当A≠0，B＝0，C＝0时，直线是y轴所在直线．【检测反馈】1. C　解析：由于直线l过点(－2，1)，且倾斜角是，则直线l的方程为x＝－2，即x＋2＝0.2. D　解析：由题意知2m2＋m－1≠0，－＝1，解得m＝或m＝－1(舍去)．3. ABD　解析：y＝ax－3a＋2(a∈R)可化为y－2＝a(x－3)，则直线y＝ax－3a＋2(a∈R)必过定点(3，2)，故A正确；令x＝0，得y＝－2，即直线y＝3x－2在y轴上的截距为－2，故B正确；x＋y＋1＝0可化为y＝－x－1，则该直线的斜率为－，即倾斜角为120°，故C错误；经过点(1，1)且在x轴和y轴上的截距都相等的直线方程为x＋y－2＝0或x－y＝0，故D正确．故选ABD. 4. (－∞，－2]∪[2，＋∞)　解析：令x＝0，得y＝2m，令y＝0，得x＝－2m.由于直线x－y＋2m＝0与两坐标轴围成的三角形的面积不小于8，故|2m|×|－2m|≥16，解得m≥2或m≤－2，故实数m的取值范围为(－∞，－2]∪[2，＋∞)．5. (1) 由直线的点斜式方程，得y－(－2)＝－(x－8)，化成一般式方程，得x＋2y－4＝0.(2) 由直线的斜截式方程，得y＝2，化成一般式方程，得y－2＝0.(3) 由直线的截距式方程，得＋＝1，化成一般式方程，得2x－y－3＝0.(4) 由直线的两点式方程，得＝，化成一般式方程得x＋y－1＝0.