所属成套资源:【同步学案】苏教版(2019)高中数学 选择性必修第一册 同步导学案
苏教版 高中数学 选择性必修第一册 活动单导学课程 2.2.1 直线与圆的位置关系(1)(含解析)
展开这是一份苏教版 高中数学 选择性必修第一册 活动单导学课程 2.2.1 直线与圆的位置关系(1)(含解析),共4页。
2.2.1 直线与圆的位置关系(1)
![]()
1. 能从“数”和“形”两个角度判断直线与圆的位置关系.
2. 会求直线与圆相切的切线方程和切线长.
3. 体会数形结合思想及分类讨论思想在位置关系中的应用.
![]()
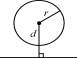
活动一 | 直线与圆位置关系的判断 |
思考
两条直线的位置关系如何判断?那直线与圆有几种位置关系?又如何去判断呢?
例1 求直线4x+3y=40和圆x2+y2=100的公共点坐标,并判断直线和圆的位置关系.
例2 求实数m的取值范围,使得直线x-my+3=0与圆x2+y2-6x+5=0分别满足:
(1) 相交;
(2) 相切;
(3) 相离.
![]()
直线与圆的位置关系 | 相离 | 相切 | 相交 | |
图示 |
|
|
| |
几何法 | d与r的大小 | d>r | d=r | d<r |
代数法 | 依据方程组
解的情况 | Δ<0 方程组 无解 | Δ=0 方程组 仅有一组解 | Δ>0 方程组有 两组不同的解 |
活动二 | 求直线和圆相切的切线方程与切线长 |
例3 自点A(-1,4)作圆(x-2)2+(y-3)2=1的切线l,求切线l的方程.
![]() 在例3中,当点A的坐标为(3,1)时,求切线l的方程.
在例3中,当点A的坐标为(3,1)时,求切线l的方程.
![]() 在例3的条件下,求切线长.
在例3的条件下,求切线长.
![]()
直线和圆相切的几何性质:
(1) d=r;
(2) 圆心、切点、切线上一点构成直角三角形;
(3) 切线垂直于过切点的半径.
![]()
1. 直线x+y+1=0与圆x2+y2-4x+2y+1=0的位置关系为( )
A. 相交 B. 相切 C. 相离 D. 不能确定
2. 若直线x-y+1=0与圆(x-a)2+y2=2有公共点,则实数a的取值范围是( )
A. [-3,-1] B. [-1,3]
C. [-3,1] D. (-∞,-3]∪[1,+∞)
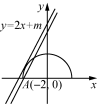
3. (多选)(2021·郴州嘉禾县第一中学月考)若直线y=2x+m与曲线y=恰有两个交点,则实数m的值可能是( )
A. B. C. 4 D. 5
4. 若过点P(-,-1)的直线l与圆x2+y2=1有公共点,则直线l的倾斜角α的取值范围是________.
5. 求圆心在直线2x+y=0上,且与直线x+y-1=0相切于点M(2,-1)的圆的标准方程.
参考答案与解析
【活动方案】
思考:设两条直线的方程分别是l1:A1x+B1y+C1=0,l2:A2x+B2y+C2=0.将这两个方程联立方程组,若方程组只有一组解,则直线l1,l2相交;若方程组无解,则直线l1,l2平行;若方程组有无数组解,则直线l1,l2重合.
直线与圆有三种位置关系,即相离、相切和相交.
方法一:几何法.
圆心到直线的距离d与圆的半径r之间的大小关系决定了直线与圆的位置关系.若d>r,则直线与圆相离;若d=r,则直线与圆相切;若d<r,则直线与圆相交.
方法二:方程法.
将直线方程和圆的方程联立方程组,方程组解的个数决定了直线与圆的位置关系.若方程组无解,即直线与圆没有公共点,则直线与圆相离;若方程组只有一组解,即直线与圆只有一个公共点,则直线与圆相切;若方程组有两组不同的解,即直线与圆有两个公共点,则直线与圆相交.
例1 直线4x+3y=40和圆x2+y2=100的公共点的坐标就是方程组的解.
解这个方程组,得
所以公共点的坐标为(10,0),.
因为直线4x+3y=40和圆x2+y2=100有两个公共点,所以直线和圆相交.
例2 圆的方程化为标准形式为(x-3)2+y2=4,
故圆心(3,0)到直线x-my+3=0的距离为d=,圆的半径为r=2.
(1) 若直线与圆相交,则d<r,即<2,
解得m<-2或m>2.
(2) 若直线与圆相切,则d=r,即=2,
解得m=2或m=-2.
(3) 若直线与圆相离,则d>r,即>2,
解得-2<m<2.
例3 当直线l垂直于x轴时,直线l:x=-1与圆相离,不满足条件;
当直线l不垂直于x轴时,可设直线l的方程为y-4=k(x+1),即kx-y+(k+4)=0.
因为直线与圆相切,
所以圆心(2,3)到直线l的距离等于圆的半径,
故=1,解得k=0或k=-,
故所求直线l的方程是y=4或3x+4y-13=0.
跟踪训练1 当直线l垂直于x轴时,直线方程为x=3,满足题意;
当直线l不垂直于x轴时,设直线l的方程为y-1=k(x-3),即kx-y+1-3k=0.
因为直线l与圆相切,
所以=1,解得k=-,
所以所求的直线方程为3x+4y-13=0.
综上,直线l的方程为x=3或3x+4y-13=0.
跟踪训练2 因为圆心C为(2,3),
所以AC==,
则切线长为==3.
【检测反馈】
1. A 解析:根据题意,得圆心为(2,-1),半径为2,则圆心到直线的距离d==<2,故直线与圆相交.
2. C 解析:由题意,得圆(x-a)2+y2=2的圆心C(a,0)到直线x-y+1=0的距离d≤,即≤,解得-3≤a≤1,故实数a的取值范围是[-3,1].
3. BC 解析:曲线y=表示圆x2+y2=4在x轴的上半部分,当直线y=2x+m与圆x2+y2=4相切时,=2,解得m=±2,当点(-2,0)在直线y=2x+m上时,m=4,所以由图可知实数m的取值范围为4≤m<2,故选BC.
4. [0°,60°] 解析:由题意,得直线l的斜率存在,设直线l的方程为y+1=k(x+),即kx-y+k-1=0,则圆心(0,0)到直线l的距离为d=≤1,解得0≤k≤,即0≤tanα≤,所以直线l的倾斜角α的取值范围为[0°,60°].
5. 因为圆与直线x+y-1=0相切,并切于点M(2,-1),所以圆心必在过点M(2,-1)且垂直于直线x+y-1=0的直线l上,
所以直线l的方程为y=x-3.
联立解得
即圆心为C(1,-2),
所以r=CM==,
所以所求圆的标准方程为(x-1)2+(y+2)2=2.
相关试卷
这是一份苏教版 高中数学 选择性必修第一册 活动单导学课程 2.4 圆的综合应用(含解析),共6页。
这是一份苏教版 高中数学 选择性必修第一册 活动单导学课程 2.3圆与圆的位置关系(含解析),共6页。试卷主要包含了 了解圆与圆之间的位置关系., 已知圆O1, 若⊙O等内容,欢迎下载使用。
这是一份苏教版 高中数学 选择性必修第一册 活动单导学课程 2.2.3 直线与圆的位置关系(3)(含解析),共4页。