


所属成套资源:【同步学案】苏教版(2019)高中数学 选择性必修第一册 同步导学案
- 苏教版 高中数学 选择性必修第一册 活动单导学课程 2.2.3 直线与圆的位置关系(3)-导学案(含解析) 试卷 0 次下载
- 苏教版 高中数学 选择性必修第一册 活动单导学课程 2.3圆与圆的位置关系-导学案(含解析) 试卷 0 次下载
- 苏教版 高中数学 选择性必修第一册 活动单导学课程 第3章圆锥曲线与方程 复 习-导学案(有答案) 试卷 0 次下载
- 苏教版 高中数学 选择性必修第一册 活动单导学课程 第5章导数及其应用5.1.1 平均变化率-导学案(有答案) 试卷 0 次下载
- 苏教版 高中数学 选择性必修第一册 活动单导学课程 第5章导数及其应用5.2.1 基本初等函数的导数-导学案(含答案) 试卷 0 次下载
苏教版 高中数学 选择性必修第一册 活动单导学课程 2.4 圆的综合应用(含解析)
展开
这是一份苏教版 高中数学 选择性必修第一册 活动单导学课程 2.4 圆的综合应用(含解析),共6页。
2.4 圆的综合应用![]() 1. 理解圆的方程,掌握圆的几何性质的应用.2. 理解点与圆、直线与圆、圆与圆的位置关系及其综合应用.3. 体会数形结合、曲线与方程思想的综合应用.
1. 理解圆的方程,掌握圆的几何性质的应用.2. 理解点与圆、直线与圆、圆与圆的位置关系及其综合应用.3. 体会数形结合、曲线与方程思想的综合应用.![]()
![]() 活动一与圆有关的最值问题例1 已知实数x,y满足方程(x-2)2+y2=3.求:(1) 的最大值和最小值;(2) y-x的最大值和最小值;(3) x2+y2的最大值和最小值.
活动一与圆有关的最值问题例1 已知实数x,y满足方程(x-2)2+y2=3.求:(1) 的最大值和最小值;(2) y-x的最大值和最小值;(3) x2+y2的最大值和最小值. ![]() 与圆有关的最值问题,常见的有以下几种类型:(1) 形如u=的最值问题,可转化为过点(x,y)和点(a,b)的动直线斜率的最值问题;(2) 形如l=ax+by的最值问题,可转化为动直线y=-x+截距的最值问题;(3) 形如m=(x-a)2+(y-b)2的最值问题,可转化为动点(x,y)到定点(a,b)的距离的平方的最值问题.
与圆有关的最值问题,常见的有以下几种类型:(1) 形如u=的最值问题,可转化为过点(x,y)和点(a,b)的动直线斜率的最值问题;(2) 形如l=ax+by的最值问题,可转化为动直线y=-x+截距的最值问题;(3) 形如m=(x-a)2+(y-b)2的最值问题,可转化为动点(x,y)到定点(a,b)的距离的平方的最值问题.![]() 已知圆C:(x+2)2+y2=1,P(x,y)为圆C上的任意一点.求:(1) 的最大值与最小值;(2) x-2y的最大值与最小值. 例2 若P是直线2x+y+10=0上的动点,PA,PB与圆x2+y2=4分别相切于A,B两点,则四边形PAOB面积的最小值为________.
已知圆C:(x+2)2+y2=1,P(x,y)为圆C上的任意一点.求:(1) 的最大值与最小值;(2) x-2y的最大值与最小值. 例2 若P是直线2x+y+10=0上的动点,PA,PB与圆x2+y2=4分别相切于A,B两点,则四边形PAOB面积的最小值为________.![]() 求面积的最值问题往往转化为距离的最值问题.
求面积的最值问题往往转化为距离的最值问题.![]() 已知P(x,y)是直线kx+y+4=0(k>0)上的一动点,PA,PB是圆C:x2+y2-2y=0的两条切线,A,B是切点,若四边形PACB的最小面积是2,则k的值为________.
已知P(x,y)是直线kx+y+4=0(k>0)上的一动点,PA,PB是圆C:x2+y2-2y=0的两条切线,A,B是切点,若四边形PACB的最小面积是2,则k的值为________. ![]() 活动二直线与圆的方程的实际应用例3 设有半径长为3 km的圆形村落,甲、乙两人同时从村落中心出发,甲向东前进而乙向北前进,甲离开村落后不久,改变前进方向,沿着与村落边界相切的直线前进,后来恰好与乙相遇.设甲、乙两人的速度都一定,且其速度比为3∶1,问:甲、乙两人在何处相遇?
活动二直线与圆的方程的实际应用例3 设有半径长为3 km的圆形村落,甲、乙两人同时从村落中心出发,甲向东前进而乙向北前进,甲离开村落后不久,改变前进方向,沿着与村落边界相切的直线前进,后来恰好与乙相遇.设甲、乙两人的速度都一定,且其速度比为3∶1,问:甲、乙两人在何处相遇? ![]() 坐标法是研究与平面图形有关的实际问题的有效手段,因此要建立适当的平面直角坐标系,用直线与圆的方程解决问题.建立平面直角坐标系时要尽可能有利于简化运算.
坐标法是研究与平面图形有关的实际问题的有效手段,因此要建立适当的平面直角坐标系,用直线与圆的方程解决问题.建立平面直角坐标系时要尽可能有利于简化运算.![]() 为适应市场需要,某地准备建一个圆形生猪储备基地(如图),它的附近有一条公路,从基地中心O向东走1 km是储备基地的边界上的点A,接着向东再走7 km到达公路上的点B,从基地中心O向北走8km到达公路的另一点C.现准备在储备基地的边界上选一点D,修建一条由点D 通往公路BC的专用线DE,求DE的最短距离.
为适应市场需要,某地准备建一个圆形生猪储备基地(如图),它的附近有一条公路,从基地中心O向东走1 km是储备基地的边界上的点A,接着向东再走7 km到达公路上的点B,从基地中心O向北走8km到达公路的另一点C.现准备在储备基地的边界上选一点D,修建一条由点D 通往公路BC的专用线DE,求DE的最短距离.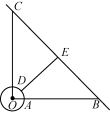
![]() 活动三过交点的圆系方程例4 求过直线x+3y-7=0与圆x2+y2+2x-2y-3=0的交点,且在两坐标轴上的四个截距之和为-8的圆的方程.
活动三过交点的圆系方程例4 求过直线x+3y-7=0与圆x2+y2+2x-2y-3=0的交点,且在两坐标轴上的四个截距之和为-8的圆的方程. ![]() 利用圆系方程求解有关圆的问题的基本思路:设所求圆的方程为圆系方程,根据已知条件建立关于参数λ的方程,根据题意解出λ并代入圆系方程即可(从实质上讲这是待定系数法).利用圆系方程的优点是避免解方程组求交点的麻烦,能简化运算,但要注意不要多解或漏解.
利用圆系方程求解有关圆的问题的基本思路:设所求圆的方程为圆系方程,根据已知条件建立关于参数λ的方程,根据题意解出λ并代入圆系方程即可(从实质上讲这是待定系数法).利用圆系方程的优点是避免解方程组求交点的麻烦,能简化运算,但要注意不要多解或漏解.![]() 对于任意实数λ,曲线(1+λ)x2+(1+λ)y2+(6-4λ)x-16-6λ=0恒过定点____________.
对于任意实数λ,曲线(1+λ)x2+(1+λ)y2+(6-4λ)x-16-6λ=0恒过定点____________.![]() 1. 圆x2+y2-4x-4y+7=0上的动点P到直线y=-x的最小距离为( )A. 2-1 B. 2-1 C. 2 D. 2+12. 已知实数x,y满足x2+y2+4x-2y-4=0,则x2+y2的最大值为( )A. 15 B. 14 C. 14+6 D. 3. (多选)瑞士著名数学家欧拉在1765年提出定理:三角形的外心、重心、垂心位于同一直线上.这条直线被后人称为三角形的“欧拉线”.在平面直角坐标系中作△ABC,AB=AC=4,点B(-1,3),点C(4,-2),且其“欧拉线”与圆M:(x-3)2+y2=r2相切,则下列结论中正确的是( )A. 圆M上点到直线x-y+3=0的最小距离为2B. 圆M上点到直线x-y+3=0的最大距离为3C. 若点(x,y)在圆M上,则x+y的最小值是3-2D. 若圆(x-a-1)2+(y-a)2=8与圆M有公共点,则a的取值范围是[1-2,1+2]4. 已知圆C的方程为(x-3)2+(y-4)2=1,过直线l:3x+ay-5=0(a>0)上任意一点作圆C的切线,若切线长的最小值为,则直线l的斜率为________.5. 如图,已知圆C与y轴相切于点T(0,2),与x轴的正半轴交于点M,N(点M在点N的左侧),且MN=3.(1) 求圆C的方程;(2) 过点M任作一直线与圆O:x2+y2=4相交于A,B两点,连接AN,BN,求证:kAN+kBN为定值.
1. 圆x2+y2-4x-4y+7=0上的动点P到直线y=-x的最小距离为( )A. 2-1 B. 2-1 C. 2 D. 2+12. 已知实数x,y满足x2+y2+4x-2y-4=0,则x2+y2的最大值为( )A. 15 B. 14 C. 14+6 D. 3. (多选)瑞士著名数学家欧拉在1765年提出定理:三角形的外心、重心、垂心位于同一直线上.这条直线被后人称为三角形的“欧拉线”.在平面直角坐标系中作△ABC,AB=AC=4,点B(-1,3),点C(4,-2),且其“欧拉线”与圆M:(x-3)2+y2=r2相切,则下列结论中正确的是( )A. 圆M上点到直线x-y+3=0的最小距离为2B. 圆M上点到直线x-y+3=0的最大距离为3C. 若点(x,y)在圆M上,则x+y的最小值是3-2D. 若圆(x-a-1)2+(y-a)2=8与圆M有公共点,则a的取值范围是[1-2,1+2]4. 已知圆C的方程为(x-3)2+(y-4)2=1,过直线l:3x+ay-5=0(a>0)上任意一点作圆C的切线,若切线长的最小值为,则直线l的斜率为________.5. 如图,已知圆C与y轴相切于点T(0,2),与x轴的正半轴交于点M,N(点M在点N的左侧),且MN=3.(1) 求圆C的方程;(2) 过点M任作一直线与圆O:x2+y2=4相交于A,B两点,连接AN,BN,求证:kAN+kBN为定值.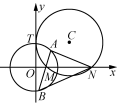 参考答案与解析【活动方案】例1 原方程表示以点(2,0)为圆心,为半径的圆.(1) 设=k,即y=kx,则当直线y=kx与圆相切时,斜率k取得最大值和最小值,此时=,解得k=±,故的最大值为,最小值为-.(2) 设y-x=b,即y=x+b,则当直线y=x+b与圆相切时,纵截距b取得最大值和最小值,此时=,解得b=-2±,故y-x的最大值为-2+,最小值为-2-.(3) x2+y2表示圆上的点与原点距离的平方.由平面几何知识知,它在原点与圆心所在的直线与圆的两个交点处取得最大值和最小值.又圆心到原点的距离为2,故(x2+y2)max=(2+)2=7+4,(x2+y2)min=(2-)2=7-4.跟踪训练 (1) 显然可以看作是点P(x,y)与点Q(1,2)连线的斜率.令k=,如图,k的最大值与最小值分别是过点Q(1,2)的圆C的两条切线的斜率.将上式整理,得kx-y-k+2=0,所以=1,解得k=,故的最大值是,最小值是.
参考答案与解析【活动方案】例1 原方程表示以点(2,0)为圆心,为半径的圆.(1) 设=k,即y=kx,则当直线y=kx与圆相切时,斜率k取得最大值和最小值,此时=,解得k=±,故的最大值为,最小值为-.(2) 设y-x=b,即y=x+b,则当直线y=x+b与圆相切时,纵截距b取得最大值和最小值,此时=,解得b=-2±,故y-x的最大值为-2+,最小值为-2-.(3) x2+y2表示圆上的点与原点距离的平方.由平面几何知识知,它在原点与圆心所在的直线与圆的两个交点处取得最大值和最小值.又圆心到原点的距离为2,故(x2+y2)max=(2+)2=7+4,(x2+y2)min=(2-)2=7-4.跟踪训练 (1) 显然可以看作是点P(x,y)与点Q(1,2)连线的斜率.令k=,如图,k的最大值与最小值分别是过点Q(1,2)的圆C的两条切线的斜率.将上式整理,得kx-y-k+2=0,所以=1,解得k=,故的最大值是,最小值是. (2) 令u=x-2y,当直线和圆C与圆相切时,u取得最大值和最小值.依题意,得=1,解得u=-2±,故x-2y的最大值是-2+,最小值是-2-.例2 8 解析:如图,因为S四边形PAOB=2S△POA,又OA⊥AP,所以S四边形PAOB=2××OA×PA=OA×=2.当且仅当OP取得最小值,四边形PAOB的面积最小,即为点O到直线2x+y+10=0的距离,故OPmin==2,故所求最小值为2×=8.
(2) 令u=x-2y,当直线和圆C与圆相切时,u取得最大值和最小值.依题意,得=1,解得u=-2±,故x-2y的最大值是-2+,最小值是-2-.例2 8 解析:如图,因为S四边形PAOB=2S△POA,又OA⊥AP,所以S四边形PAOB=2××OA×PA=OA×=2.当且仅当OP取得最小值,四边形PAOB的面积最小,即为点O到直线2x+y+10=0的距离,故OPmin==2,故所求最小值为2×=8.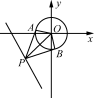 跟踪训练 2 解析:圆C:x2+y2-2y=0的圆心为(0,1),半径r=1.由圆的性质知S四边形PACB=2S△PBC.因为四边形PACB的最小面积是2,所以S△PBC的最小值为1,则×1×dmin=1(d为切线长),所以dmin=2,所以PCmin=.因为圆心到直线的距离就是PC的最小值,所以PCmin==.因为k>0,所以k=2.例3 以村落中心为坐标原点,以东西方向为x轴,南北方向为y轴,建立如图所示的平面直角坐标系.设甲向东走到点D转向到点C恰好与乙相遇,CD所在直线的方程为+=1(a>3,b>3),乙的速度为v,则甲的速度为3v.依题意,得解得所以当乙自村落中心向北前进3.75 km时,甲、乙两人相遇.
跟踪训练 2 解析:圆C:x2+y2-2y=0的圆心为(0,1),半径r=1.由圆的性质知S四边形PACB=2S△PBC.因为四边形PACB的最小面积是2,所以S△PBC的最小值为1,则×1×dmin=1(d为切线长),所以dmin=2,所以PCmin=.因为圆心到直线的距离就是PC的最小值,所以PCmin==.因为k>0,所以k=2.例3 以村落中心为坐标原点,以东西方向为x轴,南北方向为y轴,建立如图所示的平面直角坐标系.设甲向东走到点D转向到点C恰好与乙相遇,CD所在直线的方程为+=1(a>3,b>3),乙的速度为v,则甲的速度为3v.依题意,得解得所以当乙自村落中心向北前进3.75 km时,甲、乙两人相遇.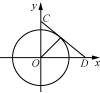 跟踪训练 以O为坐标原点,OB,OC所在直线分别为x轴和y轴,建立平面直角坐标系,则圆O的方程为x2+y2=1.因为点B(8,0),C(0,8),所以直线BC的方程为x+y=8.当O,D,E三点共线,且OE⊥BC时,DE最短,所以DE的最短距离为-1=(4-1)km.例4 设过直线与圆的交点的圆的方程为(x2+y2+2x-2y-3)+λ(x+3y-7)=0,即x2+y2+(2+λ)x+(3λ-2)y-3-7λ=0.令y=0,得x2+(2+λ)x-3-7λ=0,所以圆在x轴上的两个截距之和为-2-λ.令x=0,得y2+(3λ-2)y-3-7λ=0,所以圆在y轴上的两个截距之和为2-3λ.由题意,得-2-λ+2-3λ=-8,解得λ=2,故所求圆的方程为x2+y2+4x+4y-17=0.跟踪训练 (1,3)和(1,-3) 解析:将(1+λ)x2+(1+λ)y2+(6-4λ)x-16-6λ=0变形为λ(x2+y2-4x-6)+(x2+y2+6x-16)=0,则解得则定点为(1,3)和(1,-3).【检测反馈】1. A 解析:由题意,得圆心为(2,2),半径r=1,所以圆心到直线的距离d==2,所以圆M上的动点P到直线的最小距离为2-1.2. C 解析:由题意知圆(x+2)2+(y-1)2=9的圆心为(-2,1),半径r=3.圆心(-2,1)到坐标原点(0,0)的距离为=,故x2+y2的最大值为(3+)2=14+6.3. ACD 解析:由AB=AC,得△ABC的外心、重心、垂心均在线段BC的垂直平分线上,即△ABC的“欧拉线”即为线段BC的垂直平分线.由点B(-1,3),C(4,-2),得线段BC的中点为,且直线的BC的斜率kBC==-1,所以线段BC的垂直平分线的斜率k=1,所以线段BC的垂直平分线的方程为y-=x-,即x-y-1=0.又圆M:(x-3)2+y2=r2与△ABC的“欧拉线”相切,且圆心为(3,0),半径为r,所以点(3,0)到直线x-y-1=0的距离为==r,所以M:(x-3)2+y2=2.对于A,B,圆M的圆心(3,0)到直线x-y+3=0的距离d==3,所以圆M上的点到直线x-y+3=0的最小距离为3-=2,最大距离为3+=4,故A正确,B错误;对于C,令z=x+y,即x+y-z=0.当直线x+y-z=0与圆M相切时,z取得最值,所以圆心(3,0)到直线的距离为=,解得z=3+2或z=3-2,则x+y的最小值是3-2,故C正确;对于D,圆(x-a-1)2+(y-a)2=8的圆心为(a+1,a),半径为2.若该圆与圆M有公共点,则2-≤≤2+,即2≤(a-2)2+a2≤18,解得1-2≤a≤1+2,故D正确.故选ACD.4. - 解析:因为圆C的半径为1,切线长的最小值为,所以圆心到直线l:3x+ay-5=0(a>0)的距离d==4,所以=4,解得a=4,所以直线l的斜率为-.5. (1) 因为圆C与y轴相切于点T(0,2),可设圆心C的坐标为(m,2)(m>0),则圆C的半径为m.又MN=3,所以m2=22+=,解得m=,所以圆C的方程为+(y-2)2=.(2) 由(1),知点M(1,0),N(4,0).当直线AB与x轴重合,则kAN=kBN=0,则kAN+kBN=0;当直线AB不与x轴重合时,设直线AB的方程为x=ty+1,点A(x1,y1),B(x2,y2),联立消去x并整理,得(t2+1)y2+2ty-3=0,则Δ=4t2+12(t2+1)=16t2+12>0,所以y1+y2=-,y1y2=-,则kAN+kBN=+=+===0.综上所述,kAN+kBN=0(定值).
跟踪训练 以O为坐标原点,OB,OC所在直线分别为x轴和y轴,建立平面直角坐标系,则圆O的方程为x2+y2=1.因为点B(8,0),C(0,8),所以直线BC的方程为x+y=8.当O,D,E三点共线,且OE⊥BC时,DE最短,所以DE的最短距离为-1=(4-1)km.例4 设过直线与圆的交点的圆的方程为(x2+y2+2x-2y-3)+λ(x+3y-7)=0,即x2+y2+(2+λ)x+(3λ-2)y-3-7λ=0.令y=0,得x2+(2+λ)x-3-7λ=0,所以圆在x轴上的两个截距之和为-2-λ.令x=0,得y2+(3λ-2)y-3-7λ=0,所以圆在y轴上的两个截距之和为2-3λ.由题意,得-2-λ+2-3λ=-8,解得λ=2,故所求圆的方程为x2+y2+4x+4y-17=0.跟踪训练 (1,3)和(1,-3) 解析:将(1+λ)x2+(1+λ)y2+(6-4λ)x-16-6λ=0变形为λ(x2+y2-4x-6)+(x2+y2+6x-16)=0,则解得则定点为(1,3)和(1,-3).【检测反馈】1. A 解析:由题意,得圆心为(2,2),半径r=1,所以圆心到直线的距离d==2,所以圆M上的动点P到直线的最小距离为2-1.2. C 解析:由题意知圆(x+2)2+(y-1)2=9的圆心为(-2,1),半径r=3.圆心(-2,1)到坐标原点(0,0)的距离为=,故x2+y2的最大值为(3+)2=14+6.3. ACD 解析:由AB=AC,得△ABC的外心、重心、垂心均在线段BC的垂直平分线上,即△ABC的“欧拉线”即为线段BC的垂直平分线.由点B(-1,3),C(4,-2),得线段BC的中点为,且直线的BC的斜率kBC==-1,所以线段BC的垂直平分线的斜率k=1,所以线段BC的垂直平分线的方程为y-=x-,即x-y-1=0.又圆M:(x-3)2+y2=r2与△ABC的“欧拉线”相切,且圆心为(3,0),半径为r,所以点(3,0)到直线x-y-1=0的距离为==r,所以M:(x-3)2+y2=2.对于A,B,圆M的圆心(3,0)到直线x-y+3=0的距离d==3,所以圆M上的点到直线x-y+3=0的最小距离为3-=2,最大距离为3+=4,故A正确,B错误;对于C,令z=x+y,即x+y-z=0.当直线x+y-z=0与圆M相切时,z取得最值,所以圆心(3,0)到直线的距离为=,解得z=3+2或z=3-2,则x+y的最小值是3-2,故C正确;对于D,圆(x-a-1)2+(y-a)2=8的圆心为(a+1,a),半径为2.若该圆与圆M有公共点,则2-≤≤2+,即2≤(a-2)2+a2≤18,解得1-2≤a≤1+2,故D正确.故选ACD.4. - 解析:因为圆C的半径为1,切线长的最小值为,所以圆心到直线l:3x+ay-5=0(a>0)的距离d==4,所以=4,解得a=4,所以直线l的斜率为-.5. (1) 因为圆C与y轴相切于点T(0,2),可设圆心C的坐标为(m,2)(m>0),则圆C的半径为m.又MN=3,所以m2=22+=,解得m=,所以圆C的方程为+(y-2)2=.(2) 由(1),知点M(1,0),N(4,0).当直线AB与x轴重合,则kAN=kBN=0,则kAN+kBN=0;当直线AB不与x轴重合时,设直线AB的方程为x=ty+1,点A(x1,y1),B(x2,y2),联立消去x并整理,得(t2+1)y2+2ty-3=0,则Δ=4t2+12(t2+1)=16t2+12>0,所以y1+y2=-,y1y2=-,则kAN+kBN=+=+===0.综上所述,kAN+kBN=0(定值).
相关试卷
这是一份苏教版 高中数学 选择性必修第一册 活动单导学课程 2.3圆与圆的位置关系(含解析),共6页。试卷主要包含了 了解圆与圆之间的位置关系., 已知圆O1, 若⊙O等内容,欢迎下载使用。
这是一份苏教版 高中数学 选择性必修第一册 活动单导学课程 2.2.3 直线与圆的位置关系(3)(含解析),共4页。
这是一份苏教版 高中数学 选择性必修第一册 活动单导学课程 2.2.2 直线与圆的位置关系(2)(含解析),共5页。试卷主要包含了 理解直线与圆相交的弦长问题., 已知圆C等内容,欢迎下载使用。










