苏教版 高中数学 选择性必修第一册 活动单导学课程 第5章导数及其应用5．1.2　瞬时变化率——导数(2)-导学案（有答案）

5．1.2　瞬时变化率——导数(2)

1. 理解导数的实际意义，能熟练地求出瞬时速度和瞬时加速度．

2. 通过瞬时速度和瞬时加速度，理解瞬时变化率的概念，领悟逼近的思想．

1. (1) 物理上的平均速度是如何定义的？已知物体做运动时，它的运动规律用函数表示为s＝s(t)，现有两个时刻t0，t0＋Δt，那么从t0到t0＋Δt这段时间内，物体的平均速度是多少？

(2)  跳水运动员从10 m跳台腾空到入水的过程中，不同时刻的速度是不同的．假设t s后运动员相对于水面的高度为H(t)＝－4.9t2＋6.5t＋10.

①求运动员在t∈[2，2.1]的平均速度；

②求运动员在t∈[2，2＋Δt]的平均速度；

③求运动员在t∈[2－Δt，2]的平均速度；

④求运动员在t＝2s时的瞬时速度．

2. 瞬时速度．

结合上例给出运动物体的瞬时速度的定义：

例1　一质点的运动方程为S＝t2＋10(位移单位：m，时间单位：s)，试求该质点在t＝3 s的瞬时速度．

例2　自由落体运动的位移S(m)与时间t(s)的关系为S＝gt2(g是常数)．

(1) 分别求当t＝0.1 s，t＝2 s时的瞬时速度；

(2) 求当t＝t0 s时的瞬时速度．

　　3. 瞬时加速度．

思考

类比上述求瞬时速度的方法，思考如何求出某一时刻物体运动的瞬时加速度？

例3　已知一辆轿车在公路上作加速直线运动，假设t s时的速度为v(t)＝t2＋3，求当t＝t0 s时轿车的瞬时加速度a.

例4　已知函数f(x)＝－.

(1) 函数f(x)在区间[1，2]，[1，1.5]，[1，1.1]上的平均变化率各是多少？

(2) 函数f(x)在x＝1时的瞬时变化率是多少？

一般地，当Δx无限趋近于0时，函数f(x)的平均变化率叫作函数f(x)在x＝x0时的瞬时变化率．

1. 火车开出车站一段时间内，速度v(单位：m/s)与行驶时间t(单位：s)之间的关系是v(t)＝0.4t＋0.6t2.当t＝t0s时，火车的瞬时加速度为2.8m/s，此时t0的值为(　　)

A.   B. 2  C.   D.

2. 已知一质点运动的位移方程为S＝5－3t2，若该质点在[1，1＋Δt]内相应的平均速度为－3Δt－6，则该质点在t＝1时的瞬时速度是(　　)

A. －3  B. 3  C. 6  D. －6

3. (多选)为满足人民对美好生活的向往，环保部门要求相关企业加强污水治理，排放未达标的企业要限期整改．设企业的污水排放量W与时间t的关系为W＝f(t)，用－的大小评价在[a，b]这段时间内企业污水治理能力的强弱．已知在整改期内，甲、乙两企业的污水排放量与时间的关系如下图所示．则下列结论中正确的是(　　)

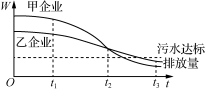
A. 在[t1，t2]这段时间内，甲企业的污水治理能力比乙企业强

B. 在t2时刻，甲企业的污水治理能力比乙企业强

C. 在t3时刻，甲、乙两企业的污水排放都已达标

D. 甲企业在[0，t1]，[t1，t2]，[t2，t3]这三段时间中，在[0，t1]时间内的污水治理能力最强

 4. 质点的速度大小按v＝t2(v，t分别为速度和时间)作加速运动，则该质点在t＝2时的瞬时加速度为________．

5. 一个做直线运动的物体，其位移S与时间t的关系是S(t)＝3t－t2.

(1) 求此物体的初速度；

(2) 求此物体在t＝2时的瞬时速度．

参考答案与解析

【活动方案】

1. (1) 在物理学中，运动物体的位移与所用时间的比称为平均速度．v＝.

(2) ①v＝＝－13.59(m/s)．

②v＝＝(－4.9Δt－13.1)m/s.

③v＝＝(4.9Δt－13.1)m/s.

④当Δt无限趋近于0时，平均速度v无限趋近于常数－13.1，所以运动员在t＝2s时的瞬时速度为－13.1m/s.

2. 一般地，如果当Δt无限趋近于0时，运动物体位移S(t)的平均变化率无限趋近于一个常数，那么这个常数称为物体在t＝t0时的瞬时速度．

例1　在3s到(3＋Δt)s的时间内，该质点的平均速度为v＝＝＝(6＋Δt)m/s，

当Δt无限趋近于0时，v无限趋近于6，即v＝6 m/s，

所以当t＝3s时该质点的瞬时速度为6m/s.

例2　(1) 在0.1s到(0.1＋Δt)s的时间内，平均速度为v＝＝＝m/s.

当Δt无限趋近于0时，v无限趋近于0.1gm/s，

所以当t＝0.1s时的瞬时速度为0.1gm/s.

同理可得当t＝2s时的瞬时速度为2gm/s.

(2) 在t0到t0＋Δt的时间内，平均速度为v＝＝＝(t0g＋gΔt)m/s，

当Δt无限趋近于0时，v无限趋近于t0gm/s，

所以当t＝t0 s时的瞬时速度为t0gm/s.

思考：首先求出速度变化的量Δv＝v(t0＋Δt)－v(t0)，和时间的变化量Δt，然后求出运动物体速度的平均变化率，当Δt无限趋近于0时，无限趋近于一个常数，这个常数称为物体在t＝t0时的瞬时加速度．

例3　在t0到t0＋Δt的时间内，轿车的平均加速度为a＝＝＝＝2t0＋Δt，　

当Δt无限趋近于0时，a无限趋近于2t0，即a＝2t0，所以当t＝t0s时轿车的瞬时加速度为2t0.

例4　(1) 函数f(x)在区间[1，2]上的平均变化率为＝3；

函数f(x)在区间[1，1.5]上的平均变化率为＝4；

函数f(x)在区间[1，1.1]上的平均变化率为＝.

(2) 在x＝1到x＝1＋Δx内，函数f(x)的平均变化率为＝，

当Δx无限趋近于0时，平均变化率无限趋近于6，

即函数f(x)在x＝1时的瞬时变化率是6.

【检测反馈】

1. B　解析：由题意，得＝＝＝0.6Δt＋0.4＋1.2t0.当Δt无限趋近于0时，无限趋近于0.4＋1.2t0，则0.4＋1.2t0＝2.8，解得t0＝2.

2. D　解析：由平均速度和瞬时速度的关系可知，质点在t＝1时的瞬时速度为Δt无限趋近于0时的平均速度，所以v＝－6.

3. ABC　解析：－表示区间端点连线斜率的相反数，在[t1，t2]这段时间内，甲的斜率比乙的斜率小，所以甲的斜率的相反数比乙的斜率相反数大，则甲企业的污水治理能力比乙企业强，故A正确；在t2时刻，甲的瞬时变化率，即切线的斜率比乙的小，所以甲切线的斜率的相反数比乙的斜率相反数大，则甲企业的污水治理能力比乙企业强，故B正确；在t3时刻，甲、乙两企业的污水排放量都在污水达标排放量以下，都已达标，故C正确；甲企业在[0，t1]，[t1，t2]，[t2，t3]这三段时间中，在[t1，t2]这段时间内的斜率最小，其相反数最大，即在[t1，t2]时间内的污水治理能力最强，故D错误．故选ABC.

4.  4　解析：＝＝Δt＋4，当Δt无限趋近于0时，无限趋近于4，所以该质点在t＝2时的瞬时加速度为4.

5. (1) 当t＝0时的速度为初速度．

在0时刻取一时间段[0，0＋Δt]，即[0，Δt]，

则＝＝＝＝3－Δt.

当Δt无限趋近于0时，无限趋近于3，

所以物体的初速度为3.

(2) 在2到2＋Δt的时间内，平均速度

v＝＝

＝

＝－1－Δt.

当Δt无限趋近于0时，v无限趋近于－1，

所以当t＝2时，物体的瞬时速度为－1.