苏教版 高中数学 选择性必修第一册 活动单导学课程 第5章导数及其应用5．3.2　极大值与极小值(1)-导学案（有答案）

这是一份苏教版 高中数学 选择性必修第一册 活动单导学课程 第5章导数及其应用5．3.2　极大值与极小值(1)（有答案），共7页。
5．3.2　极大值与极小值(1) 1. 借助几何图形直观地理解极值与极值点的概念，掌握极值与导数的关系．2. 学会绘制极值与导数关系表，进而掌握求函数极值的方法． 活动一理解函数极值的概念，理解极值与导数的关系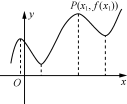1. 观察上述函数图象，回答下面的问题：(1) 函数图象在点P的左、右两侧分别有什么变化规律？  (2) 在点P附近，哪个点的位置最高？对应的函数值哪个最大？  2. 函数极值的概念．(1) 试根据上图给出函数极大值的概念：   (2) 类比给出函数极小值的概念：   (3) 极值的概念：    思考1 函数的极大值与极小值是否都唯一？极大值一定比极小值大吗？ 思考2 函数的极值点能否出现在区间端点？  思考3 在函数极大值点两侧的函数图象有什么变化规律？能否从导数出发进行研究？ 3. 函数的极值与导数的关系．结合上图探求函数的极大值与导数的关系，并填写下表： xx1左侧x1x1右侧f′(x)f′(x)____0f′(x)____0f′(x)____0f(x)单调递____取得________单调递____　　试类比探求极小值与导数的关系： xx2左侧x2x2右侧f′(x)f′(x)____0f′(x)____0f′(x)____0f(x)单调递____取得________单调递____　　思考4 若函数f(x)在x0处取得极值，则f′(x0)＝0.反过来，若f′(x0)＝0，则函数f(x)一定在x0处取得极值吗？能否举例说明？    例1　在下列函数中，函数在x＝0处取得极值的是________．(填序号)①y＝－x3；②y＝tanx－x；③y＝；④y＝－2cosx.    活动二掌握求函数极值的方法例2　求函数f(x)＝x3－4x＋的极值．           思考5 求函数的极值的一般步骤是什么？　　　求函数f(x)＝x3－3x2－9x＋5的极值．            　求函数f(x)＝的极值．   
1. 函数y＝x3－6x的极大值为(　　)A. 4  B. 3  C. －3  D. －42. 下列函数中，存在极值的是(　　)A. y＝  B. y＝x－ex  C. y＝2  D. y＝x33. (多选)若函数y＝f(x)的导函数y＝f′(x)的图象如图所示，则下列结论中正确的是(　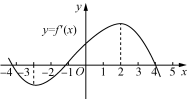　)A. 函数f(x)在区间(2，4)上单调递减B. 函数f(x)在区间(－3，－2)上单调递减C. 当x＝－3时，函数f(x)取得极小值D. 当x＝4时，函数f(x)取得极大值4. 已知函数f(x)＝xlnx，则y＝f(x)的极小值为________．5. 求下列函数的极值：(1)  y＝；(2)  y＝x－2cosx；(3)  y＝ex－ex.    参考答案与解析【活动方案】1. (1) 函数图象在点P处从左侧到右侧由“上升”变为“下降”，即函数由单调递增变为单调递减．(2) 点P的位置最高，f(x1)最大．2. (1) 一般地，若存在δ>0，当x∈(x1－δ，x1＋δ)时，都有f(x)≤f(x1)，则称f(x1)为函数f(x)的一个极大值．(2) 一般地，若存在δ>0，当x∈(x2－δ，x2＋δ)时，都有f(x)≥f(x2)，则称f(x2)为函数f(x)的一个极小值．(3) 函数的极大值、极小值统称为函数的极值．思考1：不唯一，不一定．思考2：不能思考3：图象先上升后下降，即先单调递增后单调递减．能从导数出发研究，即左侧f′(x)>0，右侧f′(x)<0.3. >　＝　<　增　极大值　减<　＝　>　减　极小值　增思考4：不一定，如函数y＝x3，导数为y′＝3x2，当x＝0时，y′＝0，但函数在x＝0处不是极值．例1　④　解析：①y′＝－3x2≤0恒成立，则函数在R上单调递减，无极值；②y′＝－1≥0恒成立，则函数在区间，k∈Z上单调递增，无极值；③y′＝－<0恒成立，则函数在区间(－∞，0)及(0，＋∞)上均为减函数，无极值；④y′＝2sinx，则函数在区间(－π，0)上单调递减，在区间(0，π)上单调递增，当x＝0时，f′(x)＝0，故当x＝0时，y＝－2cosx取得极值．例2　f′(x)＝x2－4，令f′(x)＝0，解得x＝±2，列表如下： x(－∞，－2)－2(－2，2)2(2，＋∞)f′(x)＋0－0＋f(x)↗极大值↘极小值↗所以当x＝－2时，f(x)有极大值f(－2)＝；当x＝2时，f(x)有极小值f(2)＝－5.思考5：①先求导；②令导数为0，求出x的值；③列表，根据f′(x)在f′(x)＝0的根左、右的值的符号来确定函数的极值．跟踪训练1　由题意，得f′(x)＝3x2－6x－9.令f′(x)＝0，即3x2－6x－9＝0，解得x1＝－1，x2＝3.列表如下： x(－∞，－1)－1(－1，3)3(3，＋∞)f′(x)＋0－0＋f(x)↗极大值↘极小值↗所以当x＝－1时，函数y＝f(x)有极大值f(－1)＝10；当x＝3时，函数y＝f(x)有极小值f(3) ＝－22.　跟踪训练2　由题意，得f′(x)＝＝，令f′(x)＝0，解得x＝0或x＝2.列表如下： x(－∞，0)0(0，2)2(2，＋∞)f′(x)－0＋0－f(x)↗极小值↘极大值↗所以当x＝0时，f(x)有极小值f(0)＝0；当x＝2时，f(x)有极大值f(2)＝.【检测反馈】1. A　解析：y′＝3x2－6，令y′>0，解得x>或x<－；令y′<0，解得－<x<，则当x＝－时，f(x)有极大值f(－)＝4.2. B　解析：对于A，因为y＝的定义域为(－∞，0)∪(0，＋∞)，该函数在定义域内不连续，且当x∈(－∞，0)时，该函数单调递减；当x∈(0，＋∞)时，该函数也单调递减，则该函数不存在极值，故A错误；对于B，因为y＝x－ex，所以定义域为R，且y′＝1－ex，令y′＝0，得x＝0.当x∈(－∞，0)时，y′>0；当x∈(0，＋∞)时，y′<0，故x＝0为函数y＝x－ex的极大值点，故B正确；对于C，因为y＝2是常数函数，所以该函数无极值，故C错误；对于D，因为y＝x3是R上的单调增函数，所以该函数无极值，故D错误．3. BD　解析：对于A，当x∈(2，4)时，f′(x)>0，所以函数y＝f(x)在区间(2，4)上单调递增，故A错误；对于B，当x∈(－3，－2)时，f′(x)<0，所以函数y＝f(x)在区间(－3，－2)上单调递减，故B正确；对于C，当x∈(－4，－2)时，f′(x)<0，函数y＝f(x)单调递减，无极小值，故C错误；对于D，当x＝4时，f′(x)＝0；当2<x<4时，f′(x)>0，函数y＝f(x)为增函数；当x>4时，f′(x)<0，函数y＝f(x)为减函数，故当x＝4时，f(x)取得极大值，故D正确．故选BD.4. －　解析：由题意，得f′(x)＝lnx＋1.由f′(x)>0，得x>；由f′(x)<0，得0<x<，所以函数f(x)在区间上单调递减，在区间上单调递增，所以y＝f(x)的极小值为f＝－.5. (1) y′＝，令y′＝0，得x＝或x＝－.列表如下： x(－∞，－)－(－，)，＋∞)y′－0＋0－y↘极小值↗极大值↘所以当x＝－时，函数有极小值－；当x＝时，函数有极大值.(2) y′＝1＋2sinx，令y′＝0，得x＝－＋2kπ或x＝＋2kπ，k∈Z.当x∈，k∈Z时，函数单调递减；当x∈，k∈Z时，函数单调递增；则当x＝－＋2kπ时，函数取得极小值－＋2kπ－，k∈Z；当x＝＋2kπ时，函数取得极大值＋2kπ＋，k∈Z.(3) y′＝ex－e，令y′＝0，得x＝1.当x∈(－∞，1)时，y′<0，函数单调递减；当x∈(1，＋∞)时，y′>0，函数单调递增，故当x＝1时，f(x)有极小值e－e＝0.