苏教版 高中数学 选择性必修第一册 活动单导学课程 第5章导数及其应用5．3.3　最大值与最小值(1)-导学案（有答案

这是一份苏教版 高中数学 选择性必修第一册 活动单导学课程 第5章导数及其应用5．3.3　最大值与最小值(1)（有答案，共6页。
5．3.3　最大值与最小值(1) 1. 理解最值的概念，掌握极值与最值的联系与区别．2. 能熟练、准确地求函数的最值．3.  初步掌握解决与最值有关的求参、恒成立、方程根、函数图象等问题的方法． 活动一掌握最值的概念，理解极值与最值的联系与区别1. (1) 复习巩固：极值的概念与极值的求法：   (2) 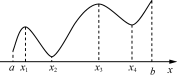最值的概念：    (3) 观察上述函数图象，探究如何求函数y＝f(x)在区间[a，b]上的最值，思考函数的极值与最值有什么联系与区别．    2. 结合上例，试给出求函数f(x)在区间[a，b]上最值的一般步骤．     活动二掌握求函数最值的方法例1　求函数f(x)＝x2－4x＋3在区间[－1，4]上的最大值与最小值．         思考1 若将区间[－1，4]改为区间(－1，4)，结果会怎样？  例2　求函数f(x)＝x＋sinx在区间[0，2π]上的最大值与最小值．         思考2 试根据上述求解过程，作出函数f(x)＝x＋sinx 在区间[0，2π]上的大致图象．         活动三掌握与函数最值有关的参数的取值范围问题例3　已知函数f(x)＝ax3－6ax2＋b，是否存在实数a，b，使函数f(x)在区间[－1，2]上取得最大值3，最小值－29？若存在，求出a，b的值；若不存在，请说明理由．        例4　设函数f(x)＝3x2＋(x>0)，x∈(0，＋∞)，f(x)≥20恒成立，求正实数a的取值范围．        
1. 函数f(x)＝x3－3x2＋2在区间[－1，1]上的最大值是(　　)A. －2  B. 0  C. 2  D. 42. 函数y＝x·lnx的最小值为(　　)A. e  B. －e  C. －  D. 3. (多选)下列结论中，正确的是(　　)A. f(x)＝x＋(x∈R)的最小值为1B. f(x)＝(x>0)的最小值为1C. f(x)＝x－ln x(x>0)的最小值为1D. f(x)＝xe(x>0)的最小值14. 函数f(x)＝(x＋1)ex的最小值是________．5. 已知函数f(x)＝x3＋3x2－9x.(1) 求曲线f(x)在点(1，－5)处的切线方程；(2) 求函数f(x)在区间[－1，2]上的最小值和最大值．     参考答案与解析【活动方案】1. (1) 略(2) 最值的概念：如果在定义域I内存在x0，使得对任意的x∈I，总有f(x)≤f(x0)(f(x)≥f(x0))，那么f(x0)为函数在定义域上的最大值(最小值)．(3) 观察函数图象可知，f(x1)，f(x3)是极大值，而f(b)>f(x3)>f(x1)，所以f(b)是最大值；f(x2)，f(x4)是极小值，而f(x2)<f(a)<f(x4)，所以f(x2)是最小值．联系：若函数f(x)在区间[a，b]上是连续的，其最值只能在极值点或端点处取得．区别：最值是整体概念，极值是局部概念．2. ①求函数f(x)在区间(a，b)上的极值；②将求得的极值与f(a)，f(b)比较，得到f(x)在区间[a，b]上的最大值与最小值．例1　由f′(x)＝2x－4＝0，得x＝2.列表如下： x－1(－1，2)2(2，4)4f′(x) －0＋ f(x)8↘－1↗3由上表可知，函数f(x)在区间[－1，4]上的最大值是8，最小值是－1.思考1：无最大值，最小值是－1.例2　由f′(x)＝＋cosx＝0，x∈[0，2π]，得x1＝，x2＝.列表如下：x0(0，)(，)(，2π)2πf′(x) ＋0－0＋ f(x)0↗＋↘－↗π 由上表可知，函数f(x)在区间[0，2π]上的最大值是π，最小值是0.思考2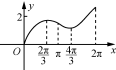：例3　显然a＝0不符合题意．f′(x)＝3ax2－12ax＝3ax(x－4)．①若a>0，由f′(x)>0，得x<0或x>4，所以函数f(x)在区间[－1，0]上单调递增，在区间(0，2]上单调递减，所以f(x)max＝f(0)＝b＝3.又f(－1)＝3－7a，f(2)＝3－16a，所以f(x)min＝f(2)＝3－16a＝－29，解得a＝2；②若a<0，由f′(x)>0，得0<x<4，所以函数f(x)在区间[－1，0]上单调递减，在区间(0，2]上单调递增，所以f(x)min＝f(0)＝b＝－29.又f(－1)＝－7a－29，f(2)＝－16a－29，所以f(x)max＝f(2)＝－16a－29＝3，解得a＝－2.综上，a＝2，b＝3或a＝－2，b＝－29.例4　由题意，得3x2＋≥20在区间(0，＋∞)上恒成立，即a≥x3(20－3x2)在区间(0，＋∞)上恒成立．令h(x)＝20x3－3x5，x>0，则h′(x)＝60x2－15x4.由h′(x)>0，得－2<x<2，所以函数h(x)在区间(0，2)上单调递增，在区间(2，＋∞)上单调递减，所以h(x)max＝h(2)＝20×23－3×25＝64，所以a≥64.综上，正实数a的取值范围是[64，＋∞)．【检测反馈】1. C　解析：由f′(x)＝3x2－6x>0，得x<0或x>2，所以函数f(x)在区间[－1，0)上单调递增，在区间[0，1]上单调递减，所以f(x)max＝f(0)＝2.2. C　解析：由题意，得y′＝lnx＋1.由y′＝lnx＋1>0，得x>；由y′＝lnx＋1<0，得0<x<，所以函数y＝x·lnx在区间上单调递减，在区间上单调递增，所以当x＝时，函数y＝x·lnx有极小值，也是最小值为·ln＝－.3. AC　解析：对于A，f(x)＝x＋(x∈R)，则f′(x)＝1－＝，所以函数f(x)在区间(－∞，0)上单调递减，在区间(0，＋∞)上单调递增，故函数f(x)的最小值为f(0)＝1，故A正确；对于B，f(x)＝(x>0)，则f′(x)＝，所以函数f(x)在区间(0，1)上单调递减，在区间(1，＋∞)上单调递增，故函数f(x)的最小值为f(1)＝e，故B错误；对于C，f(x)＝x－ln x(x>0)，则f′(x)＝1－＝，所以函数f(x)在区间(0，1)上单调递减，在区间(1，＋∞)上单调递增，故函数f(x)的最小值为f(1)＝1，故C正确；对于D，f(x)＝xe(x>0)，则f′(x)＝e＋x·e·＝，所以函数f(x)在区间(0，1)上单调递减，在区间(1，＋∞)上单调递增，故函数f(x)的最小值为f(1)＝e，故D错误．故选AC.4. －　解析：由题意，得f′(x)＝(x＋2)ex，当x>－2时，f′(x)>0，函数f(x)单调递增；当x<－2时，f′(x)<0，函数f(x)单调递减，所以当x＝－2时，函数取得极小值也是最小值，最小值为f(－2)＝(－2＋1)e－2＝－.5. (1) 因为f(x)＝x3＋3x2－9x，所以f′(x)＝3x2＋6x－9，所以f′(1)＝0，f(1)＝－5，所以曲线y＝f(x)在点(1，－5)处的切线方程为y＝－5.(2) 令f′(x)＝3(x2＋2x－3)＝0，解得x＝－3(舍去)或x＝1.列表如下： x[－1，1)1(1，2]f′(x)－0＋f(x)↘极小值↗所以函数f(x)在区间[－1，1)上单调递减，在区间(1，2]上单调递增，所以函数f(x)的极小值为f(1)＝－5.又f(－1)＝－1＋3＋9＝11，f(2)＝23＋3×22－9×2＝2，所以函数f(x)在区间[－1，2]上的最小值为－5，最大值为11.