苏教版 高中数学 选择性必修第一册 活动单导学课程 第三章圆锥曲线与方程3.1.1　椭圆的标准方程(1)-导学案（有答案）

这是一份苏教版 高中数学 选择性必修第一册 活动单导学课程 第三章圆锥曲线与方程3.1.1　椭圆的标准方程(1)（有答案），共7页。
3.1.1　椭圆的标准方程(1)1. 在具体的情景和数学实验中，掌握椭圆的定义．2. 经历椭圆标准方程的建立过程，体验求曲线方程的一般方法．3. 初步掌握用定义法和待定系数法求椭圆的标准方程． 活动一情境引入太阳系中行星的运动轨迹是椭圆．用点光源照射一个放在地面上的球，适当调整点光源的位置，球在地面上影子的外轮廓线可以是椭圆． 活动二理解椭圆的概念，推导椭圆的标准方程取一条定长的细绳，将它的两端都固定在画板的同一点，套上铅笔，拉紧绳子，移动笔尖，这时笔尖(动点)画出的轨迹是一个圆．如果将细绳的两端拉开一段距离，分别固定在画板中的两点F1，F2，且细绳的长度大于F1F2，套上铅笔，拉紧绳子，移动笔尖，画出的轨迹是什么曲线？在这一过程中，移动的笔尖(动点)满足的几何条件是什么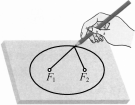？1. 椭圆的定义平面内到两个定点F1，F2的距离之和等于____________的点的轨迹叫作椭圆，____________叫作椭圆的焦点，________________叫作椭圆的焦距． 　思考1 (1) 椭圆定义中将“大于F1F2”改为“等于F1F2”的常数，其他条件不变，动点的轨迹是什么？(2) 椭圆定义中将“大于F1F2”改为“小于F1F2”的常数，其他条件不变，动点的轨迹是什么？  2. 椭圆的标准方程设椭圆的两个焦点分别为F1，F2，F1F2＝2c，椭圆上任意一点P到点F1，F2的距离之和为2a(2a>2c)．思考下列问题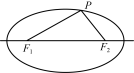：(1) 观察椭圆的形状，你认为如何建立平面直角坐标系可能使所有的椭圆方程形式简单？  (2) 椭圆上的点满足的几何条件是什么？  (3) 如何用代数式表示这个几何条件？  (4) 如何化简这个代数式？  (5) 令a2－c2＝b2(b>0)，椭圆的方程可化为什么形式？  思考2 若椭圆的焦点在y轴上，你能从焦点在x轴上的椭圆方程的结构特征猜想此时的标准方程吗？怎样推导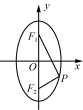？ 思考3 椭圆的标准方程有什么结构特征？思考4 两种形式椭圆的标准方程有哪些相同点？有哪些不同点？如何区分？   活动三掌握椭圆的标准方程的求法例1　已知椭圆的两个焦点分别是F1(－3，0)，F2(3，0)，椭圆上一点P到两个焦点的距离之和为10，求椭圆的标准方程．   反思与感悟 用待定系数法求椭圆标准方程的一般步骤：(1) 定位置：根据条件判断椭圆的焦点是在x轴上，还是在y轴上，还是两个坐标轴都有可能；(2) 设方程：根据上述判断设方程＋＝1(a＞b＞0)或＋＝1(a＞b＞0)或整式形式mx2＋ny2＝1(m＞0，n＞0，m≠n)；(3) 找关系：根据已知条件建立关于a，b，c(或m，n)的方程组；(4) 得方程：解方程组，将解代入所设方程，写出标准形式即为所求．　若椭圆的两个焦点的坐标分别为F1(－4，0)，F2(4，0)，且椭圆上一点P与两焦点的距离之和等于10，求椭圆的标准方程．     活动四理解椭圆的标准方程例2　求下列椭圆的焦点坐标：(1) ＋y2＝1；(2)  16x2＋9y2＝144.   反思与感悟 首先将椭圆方程化为标准方程，然后确定其焦点所在的位置，根据方程求出c的值，从而得到焦点坐标．　　　(1) 已知方程＋＝1表示焦点在y轴上的椭圆，求实数m的取值范围；(2) 若椭圆2kx2＋ky2＝1(k>0)的一个焦点为(0，－4)，求实数k的值．        1.  若椭圆＋＝1的一个焦点坐标为(1，0)，则实数m的值为(　　 )A. 1  B. 2  C. 4  D. 62. 已知椭圆＋＝1(a>b>0)的右焦点为F (3，0)，点(0，－3)在椭圆上，则椭圆的方程为(　　)A. ＋＝1  B. ＋＝1  C. ＋＝1  D. ＋＝13. (多选)已知曲线C：mx2＋ny2＝1，则下列结论中正确的是(　　)A. 若m>n>0，则曲线C是椭圆，其焦点在y轴上B. 若m＝n>0，则曲线C是圆，其半径为C. 若n >m>0，则曲线C是椭圆，其焦点在x轴上D. 若m＝0，n>0，则曲线C是两条直线4. (2021·绍兴第一中学期中)已知椭圆x2sinα－y2cosα＝1(0≤α<2π)的焦点在y轴上，则α的取值范围是________．5.  求适合下列条件的椭圆的方程：(1) 经过点P(3，0)，a＝3b；(2) 焦点为F1(0，－3)，F2(0，3)，a＝5.
参考答案与解析 【活动方案】活动二：画出的轨迹是椭圆，在这一过程中，移动的笔尖(动点)到两个定点的距离的和为定值．1. 常数(大于F1F2)　两个定点F1，F2　两个焦点间的距离思考1：(1) 动点的轨迹是线段F1F2.(2) 当距离之和小于F1F2时，动点的轨迹不存在．2. (1) 以F1，F2所在的直线为x轴，线段F1F2的垂直平分线为y轴，建立平面直角坐标系xOy.(2) PF1＋PF2＝2a(2a>2c)．(3) 由(1)中的平面直角坐标系得点F1(－c，0)，F2(c，0)．设点P(x，y)为椭圆上任意一点，由PF1＋PF2＝2a，得＋＝2a.(4) 将代数式移项，两边平方，得(x＋c)2＋y2＝4a2－4a＋(x－c)2＋y2，整理，得a2－cx＝a.两边再平方，得a4－2a2cx＋c2x2＝a2x2－2a2cx＋a2c2＋a2y2，整理，得(a2－c2)x2＋a2y2＝a2(a2－c2)．(5) ＋＝1(a>b>0)．思考2：设点P(x，y)，焦点为F1(0，c)，F2(0，－c)，则根据椭圆的定义，得PF1＋PF2＝2a，即＋＝2a，化简，得＋＝1(a>b>0)．思考3：略思考4：略例1　因为椭圆的焦点在x轴上，所以设椭圆的标准方程为＋＝1(a>b>0)．由已知，得2a＝10，即a＝5.又因为椭圆的两个焦点为F1(－3，0)，F2(3，0)，所以c＝3，所以b2＝a2－c2＝52－32＝16，故所求椭圆的标准方程为＋＝1.跟踪训练　因为椭圆的焦点在x轴上，且c＝4，2a＝10，所以a＝5，b＝＝＝3，所以椭圆的标准方程为＋＝1.例2　(1) 因为a2＝9，b2＝1，所以c2＝8，即c＝2，所以椭圆的焦点坐标为(2，0)，(－2，0)．(2) 将椭圆方程化为标准方程＋＝1，所以a2＝16，b2＝9，c＝，所以椭圆的焦点坐标为(0，)，(0，－)．跟踪训练　(1) 因为方程表示焦点在y轴上的椭圆，所以解得8<m<25，故实数m的取值范围是(8，25)．(2) 将椭圆方程化成标准方程＋＝1，因为椭圆的一个焦点坐标为(0，－4)，所以－＝16，解得k＝，故实数k的值为.【检测反馈】1. C　解析：由题意，得5－m＝1，解得m＝4.2. D　3. ACD　解析：对于A，若m>n>0，则mx2＋ny2＝1可化为＋＝1.因为m>n>0，所以0<<，即曲线C表示焦点在y轴上的椭圆，故A正确；对于B，若m＝n>0，则mx2＋ny2＝1可化为x2＋y2＝，此时曲线C表示圆心在原点，半径为的圆，故B不正确；对于C，同A可知正确；对于D，若m＝0，n>0，则mx2＋ny2＝1可化为y2＝，y＝±，此时曲线C表示平行于x轴的两条直线，故D正确．故选ACD.4. 　解析：椭圆x2sinα－y2cosα＝1(0≤α<2π)化为标准方程，得＋＝1.因为它的焦点在y轴上，所以所以0<－cosα<sinα.因为0≤α<2π，所以<α<.5. (1) 当焦点在x轴上时，由椭圆过点P(3，0)知a＝3.因为a＝3b，所以b＝1，所以椭圆的方程为＋y2＝1；当焦点在y轴上时，由椭圆过点P(3，0)知b＝3.因为a＝3b，所以a＝9，所以椭圆的标准方程为＋＝1.综上所述，椭圆的方程为＋y2＝1或＋＝1.(2) 由题意知c＝3，a＝5，且焦点在y轴上，所以b2＝16，所以椭圆的方程为＋＝1.