

所属成套资源:【同步学案】苏教版(2019)高中数学 选择性必修第一册 同步导学案
- 苏教版 高中数学 选择性必修第一册 活动单导学课程 第三章圆锥曲线与方程3.2.1双曲线的标准方程(1)-导学案(有答案) 试卷 0 次下载
- 苏教版 高中数学 选择性必修第一册 活动单导学课程 第三章圆锥曲线与方程3.2.1双曲线的标准方程(2)-导学案(有答案) 试卷 0 次下载
- 苏教版 高中数学 选择性必修第一册 活动单导学课程 第三章圆锥曲线与方程3.2.2双曲线的几何性质(2)-导学案(有答案) 试卷 0 次下载
- 苏教版 高中数学 选择性必修第一册 活动单导学课程 第三章圆锥曲线与方程3.3.1抛物线的标准方程-导学案(有答案) 试卷 0 次下载
- 苏教版 高中数学 选择性必修第一册 活动单导学课程 第三章圆锥曲线与方程3.3.2 抛物线的几何性质(2)-导学案(有答案) 试卷 0 次下载
苏教版 高中数学 选择性必修第一册 活动单导学课程 第三章圆锥曲线与方程3.2.2双曲线的几何性质(1)-导学案(有答案)
展开
这是一份苏教版 高中数学 选择性必修第一册 活动单导学课程 第三章圆锥曲线与方程3.2.2双曲线的几何性质(1)(有答案),共5页。
3.2.2 双曲线的几何性质(1)![]() 1. 了解双曲线的简单几何性质,如范围、对称性、顶点、渐近线和离心率.2. 感受运用方程研究几何性质的思想方法.
1. 了解双曲线的简单几何性质,如范围、对称性、顶点、渐近线和离心率.2. 感受运用方程研究几何性质的思想方法.![]()
![]() 活动一掌握双曲线的几何性质
活动一掌握双曲线的几何性质![]() 在建立了双曲线的标准方程之后,可以通过方程继续研究双曲线的几何性质.探究:类比椭圆几何性质的研究,能否根据双曲线的标准方程-=1(a>0,b>0)得到双曲线的范围、对称性、顶点等几何性质?1. (1) 范围: (2) 根据双曲线方程-=1(a>0,b>0),你能发现双曲线的范围还受怎样的限制? 2. 对称性: 3. 顶点: 双曲线的实轴: 双曲线的虚轴: 试探究 a,b,c的几何意义. 4. (1) 我们已经知道,双曲线的范围在以直线y=x和y=-x为边界的平面区域内,那么从x,y的变化趋势看,双曲线-=1(a>0,b>0)与直线y=±x具有怎样的关系?(2) 渐近线:(3) 由图形可知,双曲线的渐近线能否看成某个矩形的对角线所在直线? (4) 比较双曲线的标准方程与其渐近线方程,如何快捷地得到双曲线的渐近线方程? (5) 什么是等轴双曲线?其渐近线方程是什么? 5. 离心率:椭圆的离心率反映图形的“扁”的程度,那么在双曲线中,离心率是否也与双曲线的形状有关?
在建立了双曲线的标准方程之后,可以通过方程继续研究双曲线的几何性质.探究:类比椭圆几何性质的研究,能否根据双曲线的标准方程-=1(a>0,b>0)得到双曲线的范围、对称性、顶点等几何性质?1. (1) 范围: (2) 根据双曲线方程-=1(a>0,b>0),你能发现双曲线的范围还受怎样的限制? 2. 对称性: 3. 顶点: 双曲线的实轴: 双曲线的虚轴: 试探究 a,b,c的几何意义. 4. (1) 我们已经知道,双曲线的范围在以直线y=x和y=-x为边界的平面区域内,那么从x,y的变化趋势看,双曲线-=1(a>0,b>0)与直线y=±x具有怎样的关系?(2) 渐近线:(3) 由图形可知,双曲线的渐近线能否看成某个矩形的对角线所在直线? (4) 比较双曲线的标准方程与其渐近线方程,如何快捷地得到双曲线的渐近线方程? (5) 什么是等轴双曲线?其渐近线方程是什么? 5. 离心率:椭圆的离心率反映图形的“扁”的程度,那么在双曲线中,离心率是否也与双曲线的形状有关? ![]() 标准方程-=1(a>0,b>0)-=1(a>0,b>0)图 形
标准方程-=1(a>0,b>0)-=1(a>0,b>0)图 形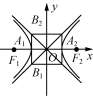
 焦点坐标 范 围 对称性 顶点坐标 离心率 渐近线方程
焦点坐标 范 围 对称性 顶点坐标 离心率 渐近线方程 ![]() 活动二掌握双曲线的几何性质例1 求双曲线-=1 的实轴长、虚轴长、焦点和顶点坐标、离心率及渐近线方程.
活动二掌握双曲线的几何性质例1 求双曲线-=1 的实轴长、虚轴长、焦点和顶点坐标、离心率及渐近线方程. ![]() 求双曲线-=1 的实轴长、虚轴长、焦点和顶点坐标、离心率及渐近线方程.
求双曲线-=1 的实轴长、虚轴长、焦点和顶点坐标、离心率及渐近线方程. ![]() 活动三掌握双曲线几何性质的简单应用例2 已知双曲线焦点在y轴上,焦距为16,离心率为,求双曲线的标准方程.
活动三掌握双曲线几何性质的简单应用例2 已知双曲线焦点在y轴上,焦距为16,离心率为,求双曲线的标准方程. ![]() 若去掉条件中的“焦点在y轴上”,结果如何? 例3 如果双曲线的渐近线方程为y=±3x,且经过点(-,6),求双曲线的标准方程.
若去掉条件中的“焦点在y轴上”,结果如何? 例3 如果双曲线的渐近线方程为y=±3x,且经过点(-,6),求双曲线的标准方程. ![]() 1. 设双曲线-=1(a>0)的渐近线方程为3x±2y=0,则a的值为( )A. 4 B. 3 C. 2 D. 12. 已知双曲线C:-=1(a>0,b>0)的离心率为,焦点到渐近线的距离为3,则双曲线C的实轴长为( )A. B. 3 C. 2 D. 63. (多选)已知双曲线x2-y2=1,F1,F2为其两个焦点,P为双曲线上的一点,若PF1⊥PF2,则下列结论中正确的是( )A. 焦点坐标为(1,0),(-1,0) B. PF1·PF2=2C. PF1+PF2=2 D. S△PF1F2=24. 已知F1,F2为双曲线C:x2-y2=1的左、右焦点,点P在双曲线C上,∠F1PF2=60°,则PF1·PF2=________.5. 若A(10,2)是双曲线my2-4x2+4m=0上的点,试求该双曲线的实轴长、虚轴长、焦距、焦点坐标、顶点坐标、离心率和渐近线方程. 参考答案与解析 【活动方案】探究:1. (1) x≥a或x≤-a(2) 由双曲线的标准方程-=1,得->0,即>0,从而或所以双曲线还应在上面两个不等式组表示的平面区域内,也就是以直线y=x和y=-x为边界的平面区域内.2. 双曲线关于x轴、y轴和原点都是对称的.3. 顶点:A1(-a,0),A2(a,0).双曲线的实轴:线段A1A2.双曲线的虚轴:B1(0,-b),B2(0,b),线段B1B2.a的几何意义:双曲线的实半轴长,b的几何意义:双曲线的虚半轴长,c的几何意义:双曲线的半焦距.4. (1) 随着x的增大,双曲线在第一象限内的点在直线y=x的下方且无限接近于这条直线;在第三象限内,双曲线上的点在直线y=x的上方且无限接近于这条直线.根据对称性,直线y=-x也有相同的性质.(2) 直线y=±x叫作双曲线-=1(a>0,b>0)的渐近线.(3) 能.直线x=±a和y=±b所围成的矩形.(4) 若双曲线的焦点在x轴上,则双曲线的渐近线方程为y=±x;若双曲线的焦点在y轴上,则双曲线的渐近线方程为y=±x.(5) 实轴和虚轴等长的双曲线叫作等轴双曲线,y=±x.5. 焦距与实轴长的比叫作双曲线的离心率.离心率越大,开口越大.小结 略例1 由题意,得a2=4,b2=3,则c2=4+3=7,所以a=2,b=,c=,所以实轴长为4,虚轴长为2,焦点坐标为(-,0),(,0),顶点坐标为(-2,0),(2,0),离心率e==,渐近线方程为y=±x.跟踪训练 实轴长为4,虚轴长为2,焦点坐标为(0,),(0,-),顶点坐标为(0,2),(0,-2),离心率e==,渐近线方程为y=±x.例2 由题意,得2c=16,所以c=8.由e==,得a=6,则b2=c2-a2=64-36=28,所以双曲线的标准方程为-=1.跟踪训练 当焦点在x轴上时,双曲线的标准方程为-=1;当焦点在y轴上时,双曲线的标准方程为-=1.例3 由题意可设双曲线的方程为9x2-y2=λ(λ≠0),将点(-,6)代入方程,得λ=9×3-36=-9,所以双曲线的标准方程为-x2=1.【检测反馈】1. C 解析:由双曲线的几何性质,得双曲线-=1(a>0)的渐近线方程为y=±x.又因为渐近线方程为3x±2y=0,即y=±x,故a=2.2. D 解析:由题意,得双曲线的一条渐近线为y=-x,即bx+ay=0.根据对称性,设双曲线的右焦点为F(c,0),c>0,则c2=a2+b2,所以焦点到渐近线的距离d===b=3.又离心率e===,所以a=3,所以双曲线C的实轴长为2a=6.3. BC 解析:因为双曲线方程为x2-y2=1,所以c==,所以焦点坐标为(,0),(-,0),故A错误;设点P在双曲线的右支上,PF2=x(x>0),PF1=2+x.因为PF1⊥PF2,所以(x+2)2+x2=(2c)2=8,解得x=-1(舍去负值),所以x+2=+1,所以PF2+PF1=-1++1=2,PF2·PF1=2,S△PF1F2=PF1·PF2=1,故B,C正确,D错误.故选BC.4. 4 解析:因为F1F=PF+PF-2PF1·PF2cos60°=(PF1-PF2)2+PF1·PF2,所以PF1·PF2=4c2-4a2=4.5. 因为点A(10,2)在双曲线my2-4x2+4m=0上,所以(2)2m-4×102+4m=0,解得m=25,所以双曲线方程为25y2-4x2+100=0,即-=1,所以双曲线的焦点在x轴上,且a2=25,b2=4,c2=25+4=29,所以实轴长为2a=10,虚轴长为2b=4,焦距为2c=2,焦点坐标为(,0),(-,0),顶点坐标为(-5,0),(5,0),离心率e==,渐近线方程为y=±x.
1. 设双曲线-=1(a>0)的渐近线方程为3x±2y=0,则a的值为( )A. 4 B. 3 C. 2 D. 12. 已知双曲线C:-=1(a>0,b>0)的离心率为,焦点到渐近线的距离为3,则双曲线C的实轴长为( )A. B. 3 C. 2 D. 63. (多选)已知双曲线x2-y2=1,F1,F2为其两个焦点,P为双曲线上的一点,若PF1⊥PF2,则下列结论中正确的是( )A. 焦点坐标为(1,0),(-1,0) B. PF1·PF2=2C. PF1+PF2=2 D. S△PF1F2=24. 已知F1,F2为双曲线C:x2-y2=1的左、右焦点,点P在双曲线C上,∠F1PF2=60°,则PF1·PF2=________.5. 若A(10,2)是双曲线my2-4x2+4m=0上的点,试求该双曲线的实轴长、虚轴长、焦距、焦点坐标、顶点坐标、离心率和渐近线方程. 参考答案与解析 【活动方案】探究:1. (1) x≥a或x≤-a(2) 由双曲线的标准方程-=1,得->0,即>0,从而或所以双曲线还应在上面两个不等式组表示的平面区域内,也就是以直线y=x和y=-x为边界的平面区域内.2. 双曲线关于x轴、y轴和原点都是对称的.3. 顶点:A1(-a,0),A2(a,0).双曲线的实轴:线段A1A2.双曲线的虚轴:B1(0,-b),B2(0,b),线段B1B2.a的几何意义:双曲线的实半轴长,b的几何意义:双曲线的虚半轴长,c的几何意义:双曲线的半焦距.4. (1) 随着x的增大,双曲线在第一象限内的点在直线y=x的下方且无限接近于这条直线;在第三象限内,双曲线上的点在直线y=x的上方且无限接近于这条直线.根据对称性,直线y=-x也有相同的性质.(2) 直线y=±x叫作双曲线-=1(a>0,b>0)的渐近线.(3) 能.直线x=±a和y=±b所围成的矩形.(4) 若双曲线的焦点在x轴上,则双曲线的渐近线方程为y=±x;若双曲线的焦点在y轴上,则双曲线的渐近线方程为y=±x.(5) 实轴和虚轴等长的双曲线叫作等轴双曲线,y=±x.5. 焦距与实轴长的比叫作双曲线的离心率.离心率越大,开口越大.小结 略例1 由题意,得a2=4,b2=3,则c2=4+3=7,所以a=2,b=,c=,所以实轴长为4,虚轴长为2,焦点坐标为(-,0),(,0),顶点坐标为(-2,0),(2,0),离心率e==,渐近线方程为y=±x.跟踪训练 实轴长为4,虚轴长为2,焦点坐标为(0,),(0,-),顶点坐标为(0,2),(0,-2),离心率e==,渐近线方程为y=±x.例2 由题意,得2c=16,所以c=8.由e==,得a=6,则b2=c2-a2=64-36=28,所以双曲线的标准方程为-=1.跟踪训练 当焦点在x轴上时,双曲线的标准方程为-=1;当焦点在y轴上时,双曲线的标准方程为-=1.例3 由题意可设双曲线的方程为9x2-y2=λ(λ≠0),将点(-,6)代入方程,得λ=9×3-36=-9,所以双曲线的标准方程为-x2=1.【检测反馈】1. C 解析:由双曲线的几何性质,得双曲线-=1(a>0)的渐近线方程为y=±x.又因为渐近线方程为3x±2y=0,即y=±x,故a=2.2. D 解析:由题意,得双曲线的一条渐近线为y=-x,即bx+ay=0.根据对称性,设双曲线的右焦点为F(c,0),c>0,则c2=a2+b2,所以焦点到渐近线的距离d===b=3.又离心率e===,所以a=3,所以双曲线C的实轴长为2a=6.3. BC 解析:因为双曲线方程为x2-y2=1,所以c==,所以焦点坐标为(,0),(-,0),故A错误;设点P在双曲线的右支上,PF2=x(x>0),PF1=2+x.因为PF1⊥PF2,所以(x+2)2+x2=(2c)2=8,解得x=-1(舍去负值),所以x+2=+1,所以PF2+PF1=-1++1=2,PF2·PF1=2,S△PF1F2=PF1·PF2=1,故B,C正确,D错误.故选BC.4. 4 解析:因为F1F=PF+PF-2PF1·PF2cos60°=(PF1-PF2)2+PF1·PF2,所以PF1·PF2=4c2-4a2=4.5. 因为点A(10,2)在双曲线my2-4x2+4m=0上,所以(2)2m-4×102+4m=0,解得m=25,所以双曲线方程为25y2-4x2+100=0,即-=1,所以双曲线的焦点在x轴上,且a2=25,b2=4,c2=25+4=29,所以实轴长为2a=10,虚轴长为2b=4,焦距为2c=2,焦点坐标为(,0),(-,0),顶点坐标为(-5,0),(5,0),离心率e==,渐近线方程为y=±x.





