苏教版 高中数学 选择性必修第一册 活动单导学课程 第三章圆锥曲线与方程3．5.2　直线与圆锥曲线的位置关系(2)-导学案（有答案）

这是一份苏教版 高中数学 选择性必修第一册 活动单导学课程 第三章圆锥曲线与方程3．5.2　直线与圆锥曲线的位置关系(2)（有答案），共6页。
3．5.2　直线与圆锥曲线的位置关系(2)1. 利用直线与圆锥曲线的位置关系，解决简单的综合问题．2. 体会方程思想和数形结合思想在圆锥曲线问题中的应用． 活动一已知直线与圆锥曲线的位置关系，求参数的值或取值范围例1　设斜率为的直线l与椭圆＋＝1(a>b>0)交于不同的两点，且这两个交点在x轴上的射影恰好是椭圆的两个焦点，则该椭圆的离心率为(　　)A. 　  B. 　  C. 　  D.  活动二体会直线与圆锥曲线相交问题的解决方法例2　已知椭圆＋＝1的弦AB的中点M的坐标为(2，1)，求直线AB的方程．     例3　已知椭圆＋＝1(a>b>0)的一条弦所在的直线方程是x－y＋5＝0，弦的中点是M(－4，1)，则椭圆的离心率是________．反思与感悟　解决椭圆中点弦问题的两种方法：(1) 根与系数的关系法：联立直线方程和椭圆方程构成方程组，消去一个未知数，利用一元二次方程根与系数的关系以及中点坐标公式解决；(2) 点差法：利用交点在曲线上，坐标满足方程，将交点坐标分别代入椭圆方程，然后作差，构造出中点坐标和斜率的关系，具体如下：已知A(x1，y1)，B(x2，y2)是椭圆＋＝1(a>b>0)上的两个不同的点，M(x0，y0)是线段AB的中点，则由①－②，得(x－x)＋(y－y1)＝0，变形，得＝－·＝－·，即kAB＝－.  活动三直线与圆锥曲线位置关系的综合应用例4　如图，已知椭圆＋y2＝1上两个不同的点A，B关于直线y＝mx＋对称，求实数m的取值范围．       
1. 过椭圆x2＋2y2＝4的左焦点作倾斜角为的弦AB，则弦AB的长为(　　)A.   B.   C.   D. 2. 已知抛物线x2＝4y内一点P(1，1)，过点P的直线l交抛物线于A，B两点，且P为弦AB的中点，则直线l的方程为(　　)A. x＋2y－3＝0  B. x－2y＋1＝0  C. 2x－y＋1＝0  D. x＋y－2＝03. (多选)已知P是双曲线－＝1右支上的一点，F1，F2分别是双曲线的左、右焦点，O为原点，|＋|＝8，则下列结论中正确的是(　　)A. 双曲线的离心率为  B. 双曲线的渐近线方程为y＝±xC. △PF1F2的面积为36  D. 点P到该双曲线左焦点的距离为184. 已知直线x－2y－3＝0过椭圆＋＝1(a>b>0)的右焦点F，且交椭圆于A，B两点．若线段AB的中点为P，直线OP的斜率为－1，则椭圆的标准方程为____________．5. 已知抛物线C：y2＝2x，过点P(2，0)的直线l交抛物线C于A，B两点．(1) 求抛物线的焦点坐标及准线方程；(2) 求证：以线段AB为直径的圆过原点O.
参考答案与解析【活动方案】例1　C　解析：由题意知两个交点横坐标是－c，c.根据椭圆的对称性，可知直线方程为y＝x，所以两个交点分别为，，代入椭圆方程，得＋＝1，两边乘以2a2b2，得c2(2b2＋a2)＝2a2b2.因为b2＝a2－c2，所以c2(3a2－2c2)＝2a4－2a2c2，即(2a2－c2)(a2－2c2)＝0，所以＝2或＝.因为0<e<1，所以e＝＝.例2　 由椭圆的对称性，知直线AB的斜率存在，设直线AB的方程为y－1＝k(x－2)．将其代入椭圆方程并整理，得(4k2＋1)x2－8(2k2－k)x＋4(2k－1)2－16＝0.设A(x1，y1)，B(x2，y2)，则x1＋x2＝.又M为线段AB的中点，所以＝＝2，解得k＝－，所以直线AB的方程为x＋2y－4＝0.例3  　　解析：设直线x－y＋5＝0与椭圆相交于点A(x1，y1)，B(x2，y2)，则x1＋x2＝－8，y1＋y2＝2.又直线AB的斜率k＝＝1.由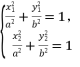两式相减，得＋＝0，所以＝－·＝1，所以＝，故椭圆的离心率e＝＝ ＝.例4　由题意知m≠0，可设直线AB的方程为y＝－x＋b.联立消去y并整理，得(＋)x2－x＋b2－1＝0.因为直线y＝－x＋b与椭圆＋y2＝1有两个不同的交点，所以Δ＝－2b2＋2＋>0.　　　　　　　①设M为AB的中点，则M，代入直线方程y＝mx＋，解得b＝－.  ②由①②，得m<－或m>，故实数m的取值范围为(－∞，－)∪(，＋∞)．【检测反馈】1. B　解析：易求得直线AB的方程为y＝(x＋)．由消去y并整理，得7x2＋12x＋8＝0.设点A(x1，y1)，B(x2，y2)，则x1＋x2＝－，x1x2＝.由弦长公式，得AB＝·|x1－x2|＝.2. B　解析：设点A(x1，y1)，B(x2，y2)，则两式相减，得(x1－x2)(x1＋x2)＝4(y1－y2)，即kAB＝＝.又AB的中点P(1，1)，所以＝，则直线l的方程为y－1＝(x－1)，即x－2y＋1＝0.3. BD　解析：因为双曲线－＝1中，a2＝25，b2＝16，则c2＝a2＋b2＝41，所以左焦点为F1(－，0)，离心率为e＝＝＝，故A错误；双曲线的渐近线方程为y＝±x，故B正确；由题意，设P(x0，y0)，x0≥5，则＝(x0，y0)，＝(－，0)，所以＋＝(x0－，y0)．因为|＋|＝8，所以(x0－)2＋y＝64.又－＝1，则y＝－16，所以(x0－)2＋－16＝64，整理，得－2x0－39＝0，解得x0＝或x0＝－(舍去)，因此|y0|＝＝，所以S△PF1F2＝F1F2·|y0|＝×2×＝32，故C错误；PF1＝＝18，故D正确．故选BD.4. ＋＝1　解析：设A(x1，y1)，B(x2，y2)，P(x0，y0)，则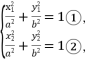①－②，得＋＝0，整理可得·＝－，即×(－1)＝－.又直线x－2y－3＝0过椭圆的右焦点F(3，0)，即c＝3，所以a2＝18，b2＝9，故椭圆的标准方程为＋＝1.5. (1) 因为抛物线C：y2＝2x，所以焦点坐标，准线方程为x＝－.(2) 设直线l的方程为x＝my＋2，联立方程组消去x并整理，得y2－2my－4＝0，设点A(x1，y1)，B(x2，y2)，则y1y2＝－4.又(y1y2)2＝4x1x2，所以x1x2＝4，则·＝x1x2＋y1y2＝0，所以⊥，故以线段AB为直径的圆过原点O. 3.6　圆锥曲线的综合应用