苏教版 高中数学 选择性必修第一册 活动单导学课程 第二章 圆与方程复习-导学案（含解析）

第二章   圆与方程复习

1. 梳理本章知识，构建知识网络．

2. 巩固圆的有关知识与思想方法．

一、 知识结构框图

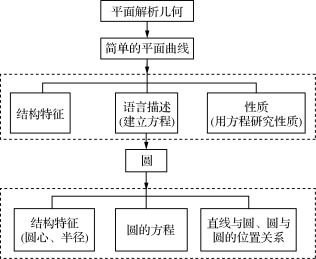
二、 圆中的相关知识

1. 圆的方程

(1) 圆的标准方程：

(x－a)2＋(y－b)2＝r2圆心为________，半径为r的圆．

(2) 圆的一般方程：

x2＋y2＋Dx＋Ey＋F＝0(D2＋E2－4F>0)圆心为________，半径为__________的圆．

(3) 若A(x1，y1)，B(x2，y2)，则以AB为直径的圆的方程为__________________．

(4) 求轨迹方程的方法：①一般法，②相关点代入法，③定义法．

2. 直线与圆的位置关系的判断方法

(1) 代数法：根据直线l与圆C的方程组成的方程组的解．有两解时，相交；有一解时，相切；无解时，相离；

(2) 几何法：根据圆心到直线的距离d与圆的半径r的大小关系：

①________相交；②________相切；③________相离．

3. 弦长的计算方法

方法一：应用圆中直角三角形：半径r，圆心到直线的距离d，弦长l具有的关系：l＝________．

方法二：利用弦长公式：设直线l：y＝kx＋b与圆的两交点为(x1，y1)，(x2，y2)，将直线方程代入圆的方程，消元后利用根与系数的关系，得弦长l＝·|x1－x2|.

4. 判断圆与圆的位置关系的方法

(1) 代数法：解两个圆的方程组成的方程组，若方程组有两组不同的实数解，则两圆相交；若方程组有两组相同的实数解，则两圆外切或内切；若方程组无实数解，则两圆相离或内含．

(2) 几何法：依据圆心距d与半径r1和r2之间的关系判断．

①当________时，两圆外离，有________条公切线；

②当________时，两圆外切，有________条公切线；

③当________时，两圆相交，有________条公切线；

④当________时，两圆内切，有________条公切线；

⑤当________时，两圆内含，有________条公切线．

三、 重要方法

1. 坐标法是研究和解决平面解析几何问题的重要方法．

2. 数形结合是本章的数学思想方法，坐标系把图形性质与代数有机地结合起来．

例1　已知圆C经过点A(2，0)，B(1，－)，且圆心C在直线y＝x上．

(1) 求圆C的方程；

(2) 过点的直线l截圆C所得的弦长为2，求直线l的方程．

例2　已知圆C：x2＋y2－2ax＋2(a－2)y＋2＝0，其中a≠1，且a∈R.求证：

(1) 当a≠1，且a∈R时，圆恒过定点；

(2) 圆心总在一条直线上，并求其方程．

例3　已知圆C的圆心为坐标原点O，且与直线l1：x－y－2＝0相切．

(1) 求圆C的方程；

(2) 若与直线l1垂直的直线l2与圆C交于不同的两点P，Q，且以PQ为直径的圆过原点，求直线l2的方程．

1. 已知直线l：x＋ay－1＝0(a∈R)是圆C：x2＋y2－4x－2y＋1＝0的对称轴．过点A(－4，a)作圆C的一条切线，切点为B，则AB的长为(　　)

A. 2  B. 4  C. 6  D. 2

2. 一条光线从点(－2，－3)射出，经y轴反射后与圆(x＋3)2＋(y－2)2＝1相切，则反射光线所在直线的斜率为(　　)

A. －或  B. －或  C. －或  D. －或－

3. (多选)下列说法中，正确的是(　　)

A. 直线mx＋4y－12＝0(m∈R)恒过定点(0，3)

B. 圆C：x2＋y2－2x－8y＋13＝0的圆心到直线4x－3y＋3＝0的距离为2

C. 圆C1：x2＋y2＋2x＝0与圆C2：x2＋y2－4x－8y＋4＝0恰有三条公切线

D. 两圆x2＋y2＋4x－4y＝0与x2＋y2＋2x－12＝0的公共弦所在的直线方程为x＋2y＋6＝0

4. 设点M(x0，1)，若在圆O：x2＋y2＝1上存在点N，使得∠OMN＝45°，则x0的取值范围是________．

5. 在平面直角坐标系xOy中，已知圆O：x2＋y2＝4及圆内一点P(1，0)，Q是圆O上的动点．以Q为圆心，QP为半径的圆Q，与圆O相交于E，F两点．

(1) 当PQ⊥x轴，且Q在第一象限时，求圆Q的方程；

(2) 若圆Q与圆x2＋y2＝r2(r>0)恒有公共点，求r的取值范围；

(3) 证明：点P到直线EF的距离为定值．

参考答案与解析

【活动方案】

活动一：略

例1　(1) 由题意，得AB的中点坐标，直线AB的斜率为，

所以直线AB的垂直平分线为x＋y＝0，与直线x－y＝0的交点为(0，0)，

所以圆心坐标为(0，0)，半径为2，

所以圆C的方程为x2＋y2＝4.

(2) 当直线l的斜率存在时，设直线l的斜率为k.

因为直线l过点，

所以直线l的方程为y－＝k(x－1)，

即y＝kx＋－k，

则圆心(0，0)到直线的距离d＝.

又圆的半径r＝2，截得的弦长为2，

则＋()2＝4，解得k＝－，

所以直线l的方程为y＝－x＋；

当直线l的斜率不存在时，直线方程为x＝1，满足题意．

综上，直线l的方程为x＝1或y＝－x＋.

例2　(1) 将方程x2＋y2－2ax＋2(a－2)y＋2＝0化为x2＋y2－4y＋2－a(2x－2y)＝0，

令解得

所以定点为(1，1)，故圆C恒过定点(1，1)．

(2) 易得圆心C的坐标为(a，2－a)，设圆心C的坐标为(x，y)，则则y＝2－x，即x＋y－2＝0，故圆心(a，2－a)总在直线x＋y－2＝0上．

例3　(1) 由已知，得圆C的半径r＝＝2，

所以圆C的方程为x2＋y2＝4.

(2) 设直线l2的方程为x＋y＋c＝0，

由已知，得△OPQ为等腰直角三角形，

则圆心到直线l2的距离为.

由点到直线的距离公式，得c＝±2，

所以直线l2的方程为x＋y＋2＝0或x＋y－2＝0.

【检测反馈】

1. C　解析：由题意，得圆心C(2，1)，半径为2，且直线l过圆心(2，1)，所以a＝－1，所以切线长AB＝＝6.

2. D　解析：由光的反射原理，知反射光线的反向延长线必过点(2，－3)．设反射光线所在直线的斜率为k，则反射光线所在直线方程为y＋3＝k(x－2)，即kx－y－2k－3＝0.又因为反射光线与圆(x＋3)2＋(y－2)2＝1相切，所以＝1，整理，得12k2＋25k＋12＝0，解得k＝－或k＝－.

3. AC　解析：对于A，当x＝0时，y＝3，所以直线过定点(0，3)，故A正确；对于B，圆C的圆心为(1，4)到直线4x－3y＋3＝0的距离为＝1，故B错误；对于C，圆C1的圆心为(－1，0)，半径为r1＝1；圆C2的圆心为(2，4)，半径为r2＝4，圆心距为＝5＝r1＋r2，所以两圆外切，则恰有三条公切线，故C正确；对于D，由两式相减并化简，得x－2y＋6＝0，故D错误．故选AC.

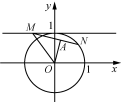
4. [－1，1]　解析：由题意知直线MN与圆O有公共点即可，即圆心O到直线MN的距离小于等于1即可，如图，过点O作OA⊥MN，垂足为A，在Rt△OMA中，因为∠OMN＝45°，所以OA＝OMsin45°＝OM≤1，解得OM≤.因为点M(x0，1)，所以OM＝≤，解得－1≤x0≤1，故x0的取值范围是[－1，1]．

5. (1) 当PQ⊥x轴时，由题意，得点Q的横坐标为x＝1，所以纵坐标满足y2＝3.

因为Q在第一象限，所以点Q(1，)，

此时PQ＝3，

所以圆Q的方程为(x－1)2＋(y－)2＝3.

(2) 因为OP＝1，OQ＝2，所以PQ∈[1，3]．

因为圆Q与圆x2＋y2＝r2(r>0)恒有公共点，且圆心之间的距离为OQ＝2，

所以|PQ－r|≤2≤PQ＋r对任意PQ∈[1，3]恒成立，

所以解得1≤r≤3，

故r的取值范围是[1，3]．

(3) 设Q(x0，y0)，则圆Q的方程为(x－x0)2＋(y－y0)2＝(x0－1)2＋y，

整理，得x2－2x0x＋y2－2y0y＝1－2x0.

又圆O：x2＋y2＝4，两式相减，

整理，得直线EF的方程为2x0x＋2y0y－2x0－3＝0，

所以点P到直线EF的距离d＝＝＝.

因为Q在圆O上，所以x＋y＝4，

所以点P到直线EF的距离d＝为定值．