


所属成套资源:【同步学案】苏教版(2019)高中数学 选择性必修第一册 同步导学案
- 苏教版 高中数学 选择性必修第一册 活动单导学课程 第三章圆锥曲线与方程3.6.2 圆锥曲线的综合应用(2)-导学案(有答案) 试卷 0 次下载
- 苏教版 高中数学 选择性必修第一册 活动单导学课程 第二章 圆与方程复习-导学案(含解析) 试卷 0 次下载
- 苏教版 高中数学 选择性必修第一册 活动单导学课程 第四章数列4.1.1 数列(1)-导学案(含答案) 试卷 0 次下载
- 苏教版 高中数学 选择性必修第一册 活动单导学课程 第四章数列4.2.1 等差数列的概念及通项公式-导学案(含答案) 试卷 0 次下载
- 苏教版 高中数学 选择性必修第一册 活动单导学课程 第四章数列4.3.1 等比数列的概念及通项公式-导学案(含答案) 试卷 0 次下载
苏教版 高中数学 选择性必修第一册 活动单导学课程 第四章数列 复 习-导学案(有答案)
展开
这是一份苏教版 高中数学 选择性必修第一册 活动单导学课程 第四章数列 复 习(有答案),共6页。
第四章数列 复 习![]() 1. 构建本章知识网络,掌握数列的定义、分类及表示方法.2. 掌握等差数列和等比数列的概念、通项公式、前n项和公式、性质及其应用.
1. 构建本章知识网络,掌握数列的定义、分类及表示方法.2. 掌握等差数列和等比数列的概念、通项公式、前n项和公式、性质及其应用.![]()
![]() 活动一本章知识网络 知识结构框图
活动一本章知识网络 知识结构框图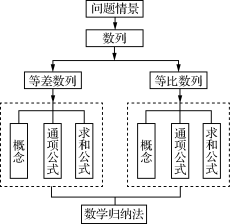
![]() 活动二基本知识提炼与整理 数列的概念及表示方法:(1) 定义:按照一定次序排列的一列数;(2) 表示方法:列表法、图象法、解析法(通项公式法和递推公式法);(3) 数列的前n项和公式与通项公式an的关系;(4) 数列是一个定义域为正整数集N*(或它的有限子集{1,2,3,…,n})的特殊函数,数列的通项公式也就是相应函数的解析式.例1 已知an=(n∈N*),求数列{an}的最大项.
活动二基本知识提炼与整理 数列的概念及表示方法:(1) 定义:按照一定次序排列的一列数;(2) 表示方法:列表法、图象法、解析法(通项公式法和递推公式法);(3) 数列的前n项和公式与通项公式an的关系;(4) 数列是一个定义域为正整数集N*(或它的有限子集{1,2,3,…,n})的特殊函数,数列的通项公式也就是相应函数的解析式.例1 已知an=(n∈N*),求数列{an}的最大项. ![]() 活动三掌握等差数列与等比数列的综合应用
活动三掌握等差数列与等比数列的综合应用 ![]() 等差数列和等比数列的比较: 等差数列等比数列定义 通项公式 前n项和公式 中项 性质 例2 已知等差数列{an}和等比数列{bn}的首项均为1,{bn}的前n项和为Sn,且a2=S2,a4=S3.(1) 求数列{an},{bn}的通项公式;(2) 设cn=an·bn,n∈N*,求数列{cn}的前n项和Tn. 例3 2020年是充满挑战的一年,但同时也是充满机遇、蓄势待发的一年.突如其来的疫情给世界带来了巨大的冲击与改变,也在客观上使得人们更加重视科技的力量和潜能.某公司一下属企业从事某种高科技产品的生产.假设该企业第一年年初有资金5 000万元,并将其全部投入生产,到当年年底资金增长了50%,预计以后每年资金年增长率与第一年相同.公司要求企业从第一年开始,每年年底上缴资金t(t≤2 500)万元,并将剩余资金全部投入下一年生产.设第n年年底企业上缴资金后的剩余资金为an万元.(1) 判断{an-2t}是否为等比数列,并说明理由;(2) 若企业每年年底上缴资金t=1 500万元,第m(m∈N)年年底企业的剩余资金超过21 000万元,求m的最小值.(lg 2≈0.301 0,lg 3≈0.477 1) 例4 已知在数列{an}中,a1=1,a2=a,an+1=k(an+an+2)对任意n∈N都成立,数列{an}的前n项和为Sn.(1) 若{an}是等差数列,求k的值;(2) 若a=1,k=-,求Sn;(3) 是否存在实数k,使数列{an}是公比不为1的等比数列,且任意相邻三项am,am+1,am+2按某种顺序排列后成等差数列?若存在,求出所有k的值;若不存在,请说明理由.
等差数列和等比数列的比较: 等差数列等比数列定义 通项公式 前n项和公式 中项 性质 例2 已知等差数列{an}和等比数列{bn}的首项均为1,{bn}的前n项和为Sn,且a2=S2,a4=S3.(1) 求数列{an},{bn}的通项公式;(2) 设cn=an·bn,n∈N*,求数列{cn}的前n项和Tn. 例3 2020年是充满挑战的一年,但同时也是充满机遇、蓄势待发的一年.突如其来的疫情给世界带来了巨大的冲击与改变,也在客观上使得人们更加重视科技的力量和潜能.某公司一下属企业从事某种高科技产品的生产.假设该企业第一年年初有资金5 000万元,并将其全部投入生产,到当年年底资金增长了50%,预计以后每年资金年增长率与第一年相同.公司要求企业从第一年开始,每年年底上缴资金t(t≤2 500)万元,并将剩余资金全部投入下一年生产.设第n年年底企业上缴资金后的剩余资金为an万元.(1) 判断{an-2t}是否为等比数列,并说明理由;(2) 若企业每年年底上缴资金t=1 500万元,第m(m∈N)年年底企业的剩余资金超过21 000万元,求m的最小值.(lg 2≈0.301 0,lg 3≈0.477 1) 例4 已知在数列{an}中,a1=1,a2=a,an+1=k(an+an+2)对任意n∈N都成立,数列{an}的前n项和为Sn.(1) 若{an}是等差数列,求k的值;(2) 若a=1,k=-,求Sn;(3) 是否存在实数k,使数列{an}是公比不为1的等比数列,且任意相邻三项am,am+1,am+2按某种顺序排列后成等差数列?若存在,求出所有k的值;若不存在,请说明理由. ![]() 1. 已知数列{an}是首项a1=4,公比q≠1的等比数列,且4a1,a5,-2a3成等差数列,则公比q等于( )A. B. -1 C. -2 D. 22. 若数列{an}满足a1=19,an+1=an-3,则数列{an}的前n项和最大时,n的值为( )A. 6 B. 7 C. 8 D. 93. (多选)已知首项为1的数列{an}的前n项和为Sn,且Sn+1=2Sn+n-1,则下列结论中正确的是( )A. 数列为等比数列 B. 数列{an}的通项公式为an=2n-1-1C. 数列为等比数列 D. 数列的前n项和为2n+2-n2-n-44. 已知在数列{an}中,a1=1,an+1=,则数列{an}的通项公式为______________.5. 在①a4+a5=-4;②a2+a6=-6;③S7=14这三个条件中任选一个,补充在下面的问题中,若问题中的k存在,则求出k的值;若k不存在,请说明理由.问题:已知等差数列{an}的前n项和为Sn,a7=3.若________,是否存在k,使得Sk-1>Sk且Sk<Sk+1?
1. 已知数列{an}是首项a1=4,公比q≠1的等比数列,且4a1,a5,-2a3成等差数列,则公比q等于( )A. B. -1 C. -2 D. 22. 若数列{an}满足a1=19,an+1=an-3,则数列{an}的前n项和最大时,n的值为( )A. 6 B. 7 C. 8 D. 93. (多选)已知首项为1的数列{an}的前n项和为Sn,且Sn+1=2Sn+n-1,则下列结论中正确的是( )A. 数列为等比数列 B. 数列{an}的通项公式为an=2n-1-1C. 数列为等比数列 D. 数列的前n项和为2n+2-n2-n-44. 已知在数列{an}中,a1=1,an+1=,则数列{an}的通项公式为______________.5. 在①a4+a5=-4;②a2+a6=-6;③S7=14这三个条件中任选一个,补充在下面的问题中,若问题中的k存在,则求出k的值;若k不存在,请说明理由.问题:已知等差数列{an}的前n项和为Sn,a7=3.若________,是否存在k,使得Sk-1>Sk且Sk<Sk+1?
参考答案与解析【活动方案】例1 因为an=,所以an+1=,所以an+1-an=.当1≤n≤11时,an+1>an,数列{an}递增;当n=12时,a13=a12=;当n≥13时,an+1<an,数列{an}递减,所以数列{an}的最大项是第12项或第13项.小结 表略例2 (1) 设等差数列{an}的公差为d,等比数列{bn}的公比为q,因为其首项均为1,且a2=S2,a4=S3,所以解得d=q=2,所以an=2n-1,bn=2n-1.(2) 设cn=(2n-1)·2n-1,所以Tn=1+3×2+5×22+…+(2n-1)·2n-1,则2Tn=1×2+3×22+5×23+…+(2n-1)·2n,两式相减,得-Tn=1+2×2+2×22+2×23+…+2×2n-1-(2n-1)×2n=1+-(2n-1)×2n=1+2n+1-4-(2n-1)×2n=(3-2n)×2n-3,所以Tn=(2n-3)·2n+3.例3 (1) 由题意,得a1=5 000(1+50%)-t=7 500-t,an+1=an(1+50%)-t=an-t.当t<2 500,即a1-2t=7 500-3t>0时,==,所以{an-2t}是以7 500-3t为首项,为公比的等比数列.当t=2 500,即a1-2t=0时,{an-2t}不是等比数列.(2) 当t=1 500时,由(1)知,an-3 000=3 000·,所以am=3 000·+3 000>21 000,即>6,所以m-1>log6==≈=≈4.42,所以m≥6,所以m的最小值为6.例4 (1) 由题意,得an+1-an=an+2-an+1,即2an+1=an+an+2,即an+1=(an+an+2),故k=.(2) 由k=-,得an+1=-(an+an+2),即2an+1=-an-an+2,an+2+an+1=-(an+1+an),故an+3+an+2=-(an+2+an+1)=an+1+an.当n是偶数时,Sn=a1+a2+a3+a4+…+an-1+an=(a1+a2)=n;当n是奇数时,因为a2+a3=-(a1+a2)=-2,所以Sn=a1+a2+a3+a4+…+an-1+an=a1+(a2+a3)+(a4+a5)+…+(an-1+an)=1+×(-2)=2-n.综上,Sn=(3) 若{an}是等比数列,则公比q==a,由题意a≠1,故am=am-1,am+1=am,am+2=am+1.①若am+1为等差中项,则2am+1=am+am+2,即2am=am-1+am+1,2a=1+a2,解得a=1(舍去);②若am为等差中项,则2am=am+1+am+2,即2am-1=am+am+1,2=a+a2,因为a≠1,解得a=-2,k====-;③若am+2为等差中项,则2am+2=am+am+1,即2am+1=am+am-1,2a2=a+1,因为a≠1,解得a=-,k==-.综上,存在实数k=-满足题意.【检测反馈】1. B 解析:由题意,得2a5=4a1-2a3,即2a1q4=4a1-2a1q2,所以q4+q2-2=0,解得q2=1.因为q≠1,所以q=-1.2. B 解析:因为a1=19,an+1-an=-3,所以数列{an}是以19为首项,-3为公差的等差数列,所以an=19+(n-1)×(-3)=22-3n,则{an}是递减数列.设{an}的前k项和最大,则有即所以≤k≤.因为k∈N*,所以k=7,所以满足条件的n的值为7.3. AD 解析:因为Sn+1=2Sn+n-1,所以==2.又S1+1=2,所以数列{Sn+n}是首项为2,公比为2的等比数列,故A正确;Sn+n=2n,则Sn=2n-n.当n≥2时,an=Sn-Sn-1=2n-1-1,但a1≠21-1-1,故B错误;由a1=1,a2=1,a3=3可得a1+1=2,a2+1=2,a3+1=4,即≠,故C错误;因为2Sn=2n+1-2n,所以2S1+2S2+…+2Sn=22-2×1+23-2×2+…+2n+1-2n=22+23+…+2n+1-2(1+2+…+n)=-2=2n+2-n2-n-4,所以数列的前n项和为2n+2-n2-n-4,故D正确.故选AD. 4. an= 解析:因为an+1=,所以==+2,所以数列是首项为1,公差为2的等差数列,所以=2n-1,所以an=.5. 若存在k,使得Sk-1>Sk且Sk<Sk+1,则ak<0,ak+1>0.设等差数列{an}的首项为a1,公差为d.若选择条件①:由得解得所以an=-9+2(n-1)=2n-11(n∈N*).令an<0,得n<,所以当k=5时,满足a5<0,a6>0,所以k=5满足题意.若选择条件②:由得解得所以an=-9+2(n-1)=2n-11(n∈N*).令an<0,得n<,所以当k=5时,满足a5<0,a6>0,所以k=5满足题意.若选择条件③:由得解得所以an=1+(n-1)=n+(n∈N*).易知an>0恒成立,所以不存在满足条件的k.






