苏教版 高中数学 选择性必修第一册 活动单导学课程 第四章数列4.1.1　数列(1)-导学案（含答案）

这是一份苏教版 高中数学 选择性必修第一册 活动单导学课程 第四章数列4.1.1　数列(1)（含答案），共7页。
4.1.1　数列(1) 1. 了解数列的概念、分类，知道数列是一类特殊的函数，会用列表法和图象法表示数列．2. 理解数列通项公式的概念，会根据通项公式写出数列的前几项，会根据简单数列的前几项写出数列的一个通项公式． 活动一了解数列的概念阅读材料，思考后面的问题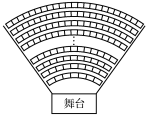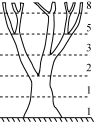：             图1                        图2某剧场有30排座位，第一排有20 个座位，从第二排起，后一排都比前一排多2个座位(如图1)，那么各排的座位数依次为20，22，24，26，28，…. ①人类在1740年发现了一颗彗星，并推算出这颗彗星每隔83年出现一次，那么从发现那次算起，这颗彗星出现的年份依次为1740，1823，1906，1989，2072，…. ②某种细胞，如果每个细胞每分钟分裂为2个，那么每过1分钟，1个细胞分裂的个数依次为1，2，4，8，16，…. ③“一尺之棰，日取其半，万世不竭”的意思为：一尺长的木棒，每日取一半，永远也取不完．如果“将一尺之棰”视为1份，那么每日剩下的部分依次为，，，，，…. ④某种树木第1年长出幼枝，第2年幼枝长成粗干，第3年粗干可生出幼枝(如图2)，那么按照这个规律，各年树木的枝干数依次为1，1，2，3，5，8，…. ⑤从1984年到2016年，我国共参加了9次夏季奥运会，各次参赛获得的金牌总数依次为15，5，16，16，28，32，51，38，26. ⑥问题1：分析上述六个问题，这些问题有什么共同的特点？  问题2：试举出与上述六个问题的数有共同特点的例子．  数列的定义：  数列的一般形式：  问题3：数列的项与它的项数分别指什么？{an}与an有何区别？  问题4：数列{an}的第n项an与项数n一定能用关系式表示吗？    活动二理解数列的通项公式　例1　已知数列的第n项an为2n－1，写出这个数列的首项、第2项和第3项．   问题5：什么叫数列的通项公式？   思考1 数列除了可以用通项公式表示，是否还有其他表示方法？  
 活动三了解数列和函数的关系例2　已知数列{an}的通项公式，写出这个数列的前5项，并作出它的图象．(1) an＝；　　　(2) an＝.      思考2 数列作为一类特殊的函数，其特殊性主要体现在哪些方面？它的图象有什么特点？   　作出下列各数列的图象．(1) 3，5，7，9，…，21；(2)  数列；(3)  数列{n2－4n＋3}．    1. 数列的通项公式实际上是一种定义域特殊的函数解析式，即an＝f(n)．2. 一个数列的通项公式在形式上可以不止一个. 活动四会用观察法写出数列的一个通项公式　　思考3 如何表示正负相间的数列对应项的符号？    例3　写出下面数列的一个通项公式，使它的前4项分别是下列各数．，－，，－，….      　　　写出以下各数列的一个通项公式：(1)  1，，，，，…；(2)  0.9，0.99，0.999，0.999 9，….   1. 下列四个数中，是数列{n(n＋1)}中的一项的是(　　)A. 380  B. 392  C. 321  D. 2322. 数列0，，，，，…的一个通项公式是(　　)A. an＝  B. an＝  C. an＝  D. an＝3. (多选)已知数列0，2，0，2，0，2，…，则前6项适合的通项公式为(　　)A. an＝1＋(－1)n  B. an＝2cosC. an＝2  D. an＝1－cos(n－1)π＋(n－1)(n－2)4. 已知数列，，，，，…，则5是它的第________项．5. 在数列{an}中，已知a1＝2，a17＝66，通项an是关于n的一次函数．(1) 求数列{an}的通项公式；(2) 88是否是数列{an}中的项？ 参考答案与解析【活动方案】问题1：都是按照一定次序排列的一列数．问题2：{1，2，3，…，n}(n∈N*)．数列的定义：按照一定次序排列的一列数叫作数列．数列的一般形式：a1，a2，a3，…，an，…，简记为{an}．问题3：数列中的每个数都叫作这个数列的项，其中a1称为数列{an}的第1项或首项，a2称为第2项，…，an称为第n项．n为数列{an}的项数．{an}表示按一定次序排列的数列，an表示数列{an}中的第n项．问题4：不一定，如当{an}是常数列时，第n项与项数n无关．例1　首项为a1＝2×1－1＝1；第2项为a2＝2×2－1＝3；第3项为a3＝2×3－1＝5.问题5：如果数列{an}的第n项与序号n之间的关系可以用一个公式来表示，那么这个公式叫作这个数列的通项公式．思考1：数列可以由通项公式来给定，也可以通过列表或图象来定义．例2　(1) a1＝，a2＝，a3＝，a4＝，a5＝，作图略．(2) a1＝－，a2＝，a3＝－，a4＝，a5＝－，作图略．思考2：数列可以看成正整数集N*(或它的有限子集{1，2，…，k})为定义域的函数，当自变量按照从小到大的顺序依次取值时，所对应的一列函数值，所以数列的图象是一系列离散的点，具有“散点图”的特点．跟踪训练　略思考3：利用(－1)n来表示．例3　an＝跟踪训练　(1) an＝　(2) an＝【检测反馈】1. A　解析：因为19×20＝380，所以380是数列{n(n＋1)}中的第19项. 2. C　解析：已知数列可化为0，，，，，…，故an＝ . 3. AC　解析：对于A，an＝1＋(－1)n取前6项，得0，2，0，2，0，2，满足条件；对于B，an＝2cos取前6项，得0，－2，0，2，0，－2，不满足条件；对于C，an＝2取前6项，得0，2，0，2，0，2，满足条件；对于D，an＝1－cos(n－1)π＋(n－1)(n－2)取前6项，得0，2，2，8，12，22，不满足条件．故选AC.4. 21　解析：由题意，得该数列的通项公式为an＝，所以令＝5，解得n＝21，故5是该数列的第21项．5. (1) 设an＝kn＋b，则由a1＝2，a17＝66，得解得所以an＝4n－2.(2) 令4n－2＝88，得n＝22.5，所以88不是数列{an}中的项．