苏教版 高中数学 选择性必修第一册 活动单导学课程 第四章数列补充2数列的通项与求和-导学案（有答案）

这是一份苏教版 高中数学 选择性必修第一册 活动单导学课程 第四章数列补充2数列的通项与求和（有答案），共6页。
补充2　数列的通项与求和(2)1. 了解通过数列的递推公式确定数列的方法．2. 掌握通过数列的前n项和确定数列通项公式的方法． 活动一用Sn与an的关系求数列的通项公式例1　(1) 已知数列{an}的前n项和Sn＝2n2－3n，试写出数列{an}的前4项；(2) 已知数列{an}的前n项和Sn＝3n－2，求数列{an}的通项公式．          　已知数列{an}的前n项和Sn＝2n2－3n＋2，求数列{an}的通项公式．        数列{an}的前n项和Sn与通项公式an的关系及其注意点：an＝注意an＝Sn－Sn－1中应附加条件n≥2，n∈N*，即实现an与Sn之间的转换时，要特别注意n的取值范围.例2　设数列{an}的前n项和Sn＝2an－4(n∈N*)，求数列{an}的通项公式．   　设数列{an}的前n项和Sn＝2an＋1－4(n∈N*)，且a1＝1.求数列{an}的通项公式．    活动二由数列的递推公式求通项公式例3　(1) 在数列{an}中，a1＝1，以后的各项由公式an＝1＋给出，写出这个数列的前5项；(2) 已知在数列{an}中，a1＝1，a2＝2，an＝3an－1＋an－2(n≥3)，写出这个数列的前5项．    例4　在数列{an}中，(1) 已知an＋1－an＝2n，a1＝1，求an；(2) 已知＝，a1＝1，求an；(3) 已知an＋1＝2an－1，a1＝1，求an.     递推公式——如果已知数列{an}的第一项(或前几项)，以及任意一项an与前面一项(或前几项)之间的关系可用一个公式来表示，那么这个公式叫作{an}的递推公式，由递推公式给出的数列称为递推数列．思考 数列的递推公式与通项公式有哪些区别与联系？
1. 已知等差数列{an}的公差不为0，{an}中的部分项ak1，ak2，ak3，…，akn，…成等比数列．若k1＝1，k2＝9，k3＝49，则k2 022等于(　　)A. 2×52 019－1  B. 2×52 020－1  C. 2×52 021－1  D. 2×52 022－1 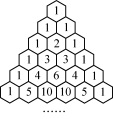2. 南宋数学家杨辉在1261年所著的《详解九章算法》中首次提出“杨辉三角”，如图所示，这是数学史上的一个伟大的成就．在“杨辉三角”中，已知每一行的数字之和构成的数列为等比数列且数列前n项和为Sn，bn＝，将数列{bn}中的整数项组成新的数列{cn}，则c2 022的值为(　　)A. 5 048  B. 5 052C. 5 046  D. 5 0533. (多选)将n2个数排成n行n列的一个数阵，如图，该数阵第一列的n个数从上到下构成以m为公差的等差数列，每一行的n个数从左到右构成以m为公比的等比数列(其中m>0)．已知a11＝2，a13＝a61＋1，记这n2个数的和为S，则下列结论中正确的有(　　)a11　a12　a13　…　a1na21　a22　a23　…　a2na31　a32　a33　…　a3n……an1　an2　an3　…　annA. m＝3  B. a67＝17×37C. aij＝(3i－1)×3j－1  D. S＝n(3n＋1)(3n－1)4. 已知在正项数列{an}中，a1＝1，a2＝2，2a＝a＋a(n≥2)，则数列{an}的通项公式为__________．5. 已知数列{an}的前n项和Sn＝2n＋1－2.(1) 求数列{an}的通项公式；(2) 设bn＝an＋an＋1，求数列{bn}的通项公式．
参考答案与解析【活动方案】例1　(1) 当n＝1时，a1＝S1＝－1；当n≥2时，an＝Sn－Sn－1＝4n－5.因为a1＝－1满足上式，所以an＝4n－5，所以a1＝－1，a2＝3，a3＝7，a4＝11.(2) 当n＝1时，a1＝S1＝1；当n≥2时，an＝Sn－Sn－1＝2×3n－1.因为a1＝1不满足上式，所以an＝跟踪训练　当n＝1时，a1＝S1＝1；当n≥2时，an＝Sn－Sn－1＝4n－5，因为a1＝1不满足上式，所以an＝例2　当n≥2时，Sn－1＝2an－1－4，所以an＝Sn－Sn－1＝2an－4－2an－1＋4，所以an＝2an－1.易知an≠0，所以＝2.因为a1＝S1＝2a1－4，所以a1＝4，所以an＝4×2n－1＝2n＋1，a1也符合，所以an＝2n＋1.跟踪训练　当n≥2时，Sn－1＝2an－4，所以an＝Sn－Sn－1＝2an＋1－2an，所以3an＝2an＋1，所以＝.当n＝1时，S1＝2a2－4＝1，即a2＝，所以＝≠，所以an＝例3　(1) a1＝1，a2＝2，a3＝，a4＝，a5＝.(2) a1＝1，a2＝2，a3＝7，a4＝23，a5＝76.例4　(1) 由an＋1－an＝2n，得an－an－1＝2(n－1)，an－1－an－2＝2(n－2)，…a2－a1＝2×1，累加，得an－a1＝2(1＋2＋…＋n－1)，即an－a1＝n2－n，所以an＝n2－n＋1.(2) 由＝，得＝，＝，…＝，累乘，得＝××…×＝，所以an＝.(3) 因为an＋1＝2an－1，所以an＋1－1＝2(an－1)．令bn＝an－1，则bn＋1＝2bn.因为b1＝a1－1＝0，所以bn＝0，所以an＝1.思考：两者均可确定数列，通项公式直接反映的是项与项数之间的关系，而递推公式反映的是数列中相邻两项(或n项)之间的关系，且递推公式包含两个部分，一是递推关系，二是初始关系，二者缺一不可．【检测反馈】1. C　解析：设等差数列{an}的公差为d，则d≠0.由题意，得a2k2＝ak1·ak3，所以a＝a1·a49，即(a1＋8d)2＝a1·(a1＋48d)，得a1＝2d，所以在等比数列ak1，ak2，ak3，…，akn，…中，公比q＝＝5.所以akn＝2d×5n－1；由akn为数列{an}的第kn项，知akn＝a1＋(kn－1)d＝d(kn＋1)，所以2d×5n－1＝d(kn＋1)，所以kn＝2×5n－1－1，所以k2 022＝2×52 021－1.2. D　解析：根据“杨辉三角”的性质可得数列的前n项和为Sn＝20＋21＋…＋2n－1＝＝2n－1，所以bn＝＝，由题意，得此数列为，，，，，，…，其中整数项为，，，，，，…，即2，3，7，8，12，13，…，所以数列cn是奇数项以5为公差，2为首项的等差数列，偶数项以5为公差，3为首项的等差数列，即c2n－1＝2＋5(n－1)＝5n－3，c2n＝3＋5(n－1)＝5n－2，所以c2 022＝5×1 011－2＝5 053.3. ACD　解析：对于A，a13＝a11·m2＝2m2，a61＝a11＋5m＝2＋5m，所以2m2＝3＋5m，又m>0，所以m＝3，故A正确；对于B，a61＝2＋5m＝17，所以a67＝a61·m6＝17×36，故B错误；对于C，ai1＝a11＋(i－1)m＝3i－1，所以aij＝ai1·mj－1＝(3i－1)·3j－1，故C正确；对于D，第i行n个数的和S′＝＝＝，所以S＝(3n－1)×＝(3n－1)×＝n(3n＋1)(3n－1)，故D正确．故选ACD.4. an＝　解析：因为2a＝a＋a(n≥2)，所以{a}是以1为首项，3为公差的等差数列，所以a＝1＋3(n－1)＝3n－2，所以an＝.当n＝1时，a1＝1符合，所以an＝.5. (1) 当n＝1时，a1＝S1＝2；当n≥2时，an＝Sn－Sn－1＝2n，a1＝2满足该式，所以an＝2n.(2) bn＝2n＋2n＋1＝3×2n.