


2022-2023学年自贡市重点中学数学七下期末学业质量监测模拟试题含答案
展开
这是一份2022-2023学年自贡市重点中学数学七下期末学业质量监测模拟试题含答案,共7页。试卷主要包含了考生要认真填写考场号和座位序号,如果a![]() 有意义,则x的取值应满足( )A.x≠4 B.x≠﹣1 C.x=4 D.x=﹣12.如图,将△ABC沿直线DE折叠后,使得点B与点A重合.已知AC=5cm,△ADC的周长为17cm,则BC的长为( )
有意义,则x的取值应满足( )A.x≠4 B.x≠﹣1 C.x=4 D.x=﹣12.如图,将△ABC沿直线DE折叠后,使得点B与点A重合.已知AC=5cm,△ADC的周长为17cm,则BC的长为( )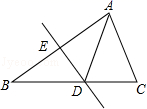 A.7cm B.10cm C.12cm D.22cm3.下列命题中,正确的是( )A.在三角形中,到三角形三边距离相等的点是三条边垂直平分线的交点B.平行四边形是轴对称图形C.三角形的中位线将三角形分成面积相等的两个部分D.一组对边平行,一组对角相等的四边形是平行四边形4.如果a<b,则下列式子错误的是( )A.a+2<b+2 B.a-3<b-3 C.-5a<-5b D.
A.7cm B.10cm C.12cm D.22cm3.下列命题中,正确的是( )A.在三角形中,到三角形三边距离相等的点是三条边垂直平分线的交点B.平行四边形是轴对称图形C.三角形的中位线将三角形分成面积相等的两个部分D.一组对边平行,一组对角相等的四边形是平行四边形4.如果a<b,则下列式子错误的是( )A.a+2<b+2 B.a-3<b-3 C.-5a<-5b D.![]() <
<![]() 5.函数y=
5.函数y=![]() 中,自变量x的取值范围是( )A.x>-3 B.x≠0 C.x>-3且x≠0 D.x≠-36.坐标平面上,有一线性函数过(-3,4)和(-7,4)两点,则此函数的图象会过( )A.第一、二象限 B.第一、四象限C.第二、三象限 D.第二、四象限7.甲、乙二人在相同情况下,各射靶10次,两人命中环数的平均数都是7,方差
中,自变量x的取值范围是( )A.x>-3 B.x≠0 C.x>-3且x≠0 D.x≠-36.坐标平面上,有一线性函数过(-3,4)和(-7,4)两点,则此函数的图象会过( )A.第一、二象限 B.第一、四象限C.第二、三象限 D.第二、四象限7.甲、乙二人在相同情况下,各射靶10次,两人命中环数的平均数都是7,方差![]() ,
,![]() ,则射击成绩较稳定的是( )A.甲 B.乙 C.一样 D.不能确定8.如图,正方形
,则射击成绩较稳定的是( )A.甲 B.乙 C.一样 D.不能确定8.如图,正方形![]() 的两边
的两边![]() ,
,![]() 分别在平面直角坐标系的
分别在平面直角坐标系的![]() 轴、
轴、![]() 轴的正半轴上正方形
轴的正半轴上正方形![]() 与正方形
与正方形![]() 是以
是以![]() 的中点
的中点![]() 为中心的位似图形,已知
为中心的位似图形,已知![]() ,
,![]() ,则正方形
,则正方形![]() 与正方形
与正方形![]() 的相似比是( )
的相似比是( )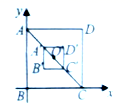 A.
A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 9.在平面直角坐标系中,一次函数y=kx+b的图象如图所示,观察图象可得( )
9.在平面直角坐标系中,一次函数y=kx+b的图象如图所示,观察图象可得( )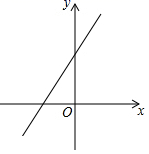 A.k>0,b>0 B.k>0,b<0 C.k<0,b>0 D.k<0,b<010.下列关于一次函数
A.k>0,b>0 B.k>0,b<0 C.k<0,b>0 D.k<0,b<010.下列关于一次函数![]() 的说法中,错误的是( )A.函数图象与
的说法中,错误的是( )A.函数图象与![]() 轴的交点是
轴的交点是![]() B.函数图象自左至右呈下降趋势,
B.函数图象自左至右呈下降趋势,![]() 随
随![]() 的增大而减小C.当
的增大而减小C.当![]() 时,
时,![]() D.图象经过第一、二、三象限11.已知一次函数的图象经过点(0,3)和(-2,0),那么直线必经过点( )A.(-4,-3) B.(4,6) C.(6,9) D.(-6,6)12.如图,四边形ABCD为矩形,依据尺规作图的痕迹,∠α与∠β的度数之间的关系为( )
D.图象经过第一、二、三象限11.已知一次函数的图象经过点(0,3)和(-2,0),那么直线必经过点( )A.(-4,-3) B.(4,6) C.(6,9) D.(-6,6)12.如图,四边形ABCD为矩形,依据尺规作图的痕迹,∠α与∠β的度数之间的关系为( )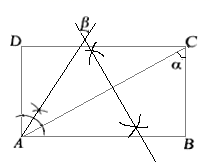 A.β= 180-α B.β=180°-
A.β= 180-α B.β=180°-![]() C.β=90°-α D.β=90°-
C.β=90°-α D.β=90°-![]() 二、填空题(每题4分,满分20分,将答案填在答题纸上)13.若不等式组
二、填空题(每题4分,满分20分,将答案填在答题纸上)13.若不等式组![]() 的解集是
的解集是![]() ,则m的值是________.14.若关于
,则m的值是________.14.若关于![]() 的方程
的方程![]() 有增根,则
有增根,则![]() 的值是___________.15.如图,Rt△ABC中,∠ACB=90°,点D为斜边AB的中点,CD=6cm,则AB的长为 cm.
的值是___________.15.如图,Rt△ABC中,∠ACB=90°,点D为斜边AB的中点,CD=6cm,则AB的长为 cm.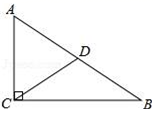 16.若
16.若![]() 有意义,则x 的取值范围是 .17.如图,梯形
有意义,则x 的取值范围是 .17.如图,梯形![]() 中,
中,![]() ,点
,点![]() 分别是
分别是![]() 的中点. 已知两底之差是6,两腰之和是12,则
的中点. 已知两底之差是6,两腰之和是12,则![]() 的周长是____.
的周长是____. 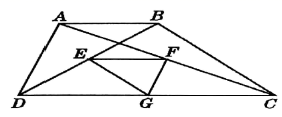 三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)18.(5分)4月12日华为新出的型号为“P30 Pro”的手机在上海召开发布会,某华为手机专卖网店抓住商机,购进10000台“P30 Pro”手机进行销售,每台的成本是4400元,在线同时向国内、国外发售.第一个星期,国内销售每台售价是5400元,共获利100万元,国外销售也售出相同数量该款手机,但每台成本增加400元,获得的利润却是国内的6倍.(1)求该店销售该款华为手机第一个星期在国外的售价是多少元?(2)受中美贸易战影响,第二个星期,国内销售每台该款手机售价在第一个星期的基础上降低m%,销量上涨5m%;国外销售每台售价在第一个星期的基础上上涨m%,并且在第二个星期将剩下的手机全部卖完,结果第二个星期国外的销售总额比国内的销售总额多6993万元,求m的值. 19.(5分) (1) 解不等式组:
三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)18.(5分)4月12日华为新出的型号为“P30 Pro”的手机在上海召开发布会,某华为手机专卖网店抓住商机,购进10000台“P30 Pro”手机进行销售,每台的成本是4400元,在线同时向国内、国外发售.第一个星期,国内销售每台售价是5400元,共获利100万元,国外销售也售出相同数量该款手机,但每台成本增加400元,获得的利润却是国内的6倍.(1)求该店销售该款华为手机第一个星期在国外的售价是多少元?(2)受中美贸易战影响,第二个星期,国内销售每台该款手机售价在第一个星期的基础上降低m%,销量上涨5m%;国外销售每台售价在第一个星期的基础上上涨m%,并且在第二个星期将剩下的手机全部卖完,结果第二个星期国外的销售总额比国内的销售总额多6993万元,求m的值. 19.(5分) (1) 解不等式组: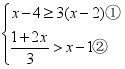 .(2)解方程:
.(2)解方程:![]() . 20.(8分)菱形ABCD在平面直角坐标系中的位置如图所示,对角线AC与BD的交点E恰好在y轴上,过点D和BC的中点H的直线交AC于点F,线段DE,CD的长是方程x2﹣9x+18=0的两根,请解答下列问题:(1)求点D的坐标;(2)若反比例函数y=
. 20.(8分)菱形ABCD在平面直角坐标系中的位置如图所示,对角线AC与BD的交点E恰好在y轴上,过点D和BC的中点H的直线交AC于点F,线段DE,CD的长是方程x2﹣9x+18=0的两根,请解答下列问题:(1)求点D的坐标;(2)若反比例函数y=![]() (k≠0)的图象经过点H,则k= ;(3)点Q在直线BD上,在直线DH上是否存在点P,使以点F,C,P,Q为顶点的四边形是平行四边形?若存在,请直接写出点P的坐标;若不存在,请说明理由.
(k≠0)的图象经过点H,则k= ;(3)点Q在直线BD上,在直线DH上是否存在点P,使以点F,C,P,Q为顶点的四边形是平行四边形?若存在,请直接写出点P的坐标;若不存在,请说明理由.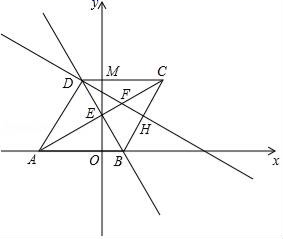 21.(10分)如图1,直线l1:y=﹣
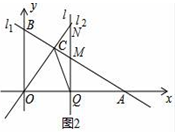
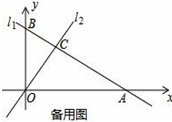
21.(10分)如图1,直线l1:y=﹣![]() x+3与坐标轴分别交于点A,B,与直线l2:y=x交于点C.(1)求A,B两点的坐标;(2)求△BOC的面积;(3)如图2,若有一条垂直于x轴的直线l以每秒1个单位的速度从点A出发沿射线AO方向作匀速滑动,分别交直线l1,l2及x轴于点M,N和Q.设运动时间为t(s),连接CQ.①当OA=3MN时,求t的值;②试探究在坐标平面内是否存在点P,使得以O、Q、C、P为顶点的四边形构成菱形?若存在,请直接写出t的值;若不存在,请说明理由.
x+3与坐标轴分别交于点A,B,与直线l2:y=x交于点C.(1)求A,B两点的坐标;(2)求△BOC的面积;(3)如图2,若有一条垂直于x轴的直线l以每秒1个单位的速度从点A出发沿射线AO方向作匀速滑动,分别交直线l1,l2及x轴于点M,N和Q.设运动时间为t(s),连接CQ.①当OA=3MN时,求t的值;②试探究在坐标平面内是否存在点P,使得以O、Q、C、P为顶点的四边形构成菱形?若存在,请直接写出t的值;若不存在,请说明理由.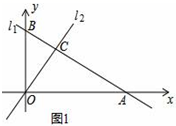
 22.(10分)某工厂新开发生产一种机器,每台机器成本y(万元)与生产数量x(台)之间满足一次函数关系(其中10≤x≤70,且为整数),函数y与自变量x的部分对应值如表 x单位:台)102030y(单位:万元/台)605550(1)求y与x之间的函数关系式;(2)市场调查发现,这种机器每月销售量z(台)与售价a(万元/台)之间满足如图所示的函数关系.①该厂第一个月生产的这种机器40台都按同一售价全部售出,请求出该厂第一个月销售这种机器的总利润.(注:利润=售价﹣成本)②若该厂每月生产的这种机器当月全部售出,则每个月生产多少台这种机器才能使每台机器的利润最大?
22.(10分)某工厂新开发生产一种机器,每台机器成本y(万元)与生产数量x(台)之间满足一次函数关系(其中10≤x≤70,且为整数),函数y与自变量x的部分对应值如表 x单位:台)102030y(单位:万元/台)605550(1)求y与x之间的函数关系式;(2)市场调查发现,这种机器每月销售量z(台)与售价a(万元/台)之间满足如图所示的函数关系.①该厂第一个月生产的这种机器40台都按同一售价全部售出,请求出该厂第一个月销售这种机器的总利润.(注:利润=售价﹣成本)②若该厂每月生产的这种机器当月全部售出,则每个月生产多少台这种机器才能使每台机器的利润最大?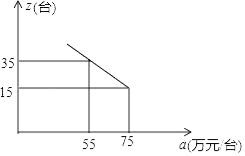 23.(12分)解不等式组:
23.(12分)解不等式组:![]() ,并把不等式组的解集在数轴上标出来
,并把不等式组的解集在数轴上标出来![]() 参考答案 一、选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.1、A2、C3、D4、C5、D6、A7、B8、A9、A10、D11、A12、D 二、填空题(每题4分,满分20分,将答案填在答题纸上)13、214、115、1.16、x≥817、1. 三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)18、(1)1800元;(2)m=1.19、 (1)
参考答案 一、选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.1、A2、C3、D4、C5、D6、A7、B8、A9、A10、D11、A12、D 二、填空题(每题4分,满分20分,将答案填在答题纸上)13、214、115、1.16、x≥817、1. 三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)18、(1)1800元;(2)m=1.19、 (1) ![]() ; (2)
; (2) ![]() .20、(1)(﹣
.20、(1)(﹣![]() ,3
,3![]() )(2)
)(2)![]() (3)(
(3)(![]() ,
,![]() )或(﹣
)或(﹣![]() ,5
,5![]() )或(
)或(![]() ,﹣
,﹣![]() )21、(1)A(6,0)B(0,3);(2)S△OBC=3;(3)①t=
)21、(1)A(6,0)B(0,3);(2)S△OBC=3;(3)①t=![]() 或
或![]() ;②t=(6+2
;②t=(6+2![]() )s或(6﹣2
)s或(6﹣2![]() )s或2s或4s时,以O、Q、C、P为顶点的四边形构成菱形.22、 (1)y=-0.5x+65(10≤x≤70,且为整数);(2)①200万元;②10.23、﹣2≤x<1,见解析.
)s或2s或4s时,以O、Q、C、P为顶点的四边形构成菱形.22、 (1)y=-0.5x+65(10≤x≤70,且为整数);(2)①200万元;②10.23、﹣2≤x<1,见解析.
相关试卷
这是一份2022-2023学年福州市重点中学数学七下期末学业质量监测试题含答案,共7页。试卷主要包含了考生必须保证答题卡的整洁,下列说法等内容,欢迎下载使用。
这是一份2022-2023学年湖南长沙北雅中学数学七下期末学业质量监测模拟试题含答案,共7页。试卷主要包含了化简2-0+得,已知直线l经过点A,式子,,,,中是分式的有等内容,欢迎下载使用。
这是一份2022-2023学年湖北省黄石十四中学数学七下期末学业质量监测模拟试题含答案,共7页。试卷主要包含了答题时请按要求用笔,已知,在中,,,高,则三角形的周长是,下列说法正确的是等内容,欢迎下载使用。








