2022-2023学年贺州市重点中学数学七年级第二学期期末学业质量监测模拟试题含答案

2022-2023学年贺州市重点中学数学七年级第二学期期末学业质量监测模拟试题

（时间：120分钟             分数：120分）

学校_______            年级_______        姓名_______

注意事项

1．考生要认真填写考场号和座位序号。

2．试题所有答案必须填涂或书写在答题卡上，在试卷上作答无效。第一部分必须用2B 铅笔作答；第二部分必须用黑色字迹的签字笔作答。

3．考试结束后，考生须将试卷和答题卡放在桌面上，待监考员收回。

一、选择题(每小题3分,共30分)

1．为了调查某校同学的体质健康状况，随机抽查了若干名同学的每天锻炼时间如表：

则关于这些同学的每天锻炼时间，下列说法错误的是（　　）

A．众数是60 B．平均数是21 C．抽查了10个同学 D．中位数是50

2．在中，，于，平分交于，则下列结论一定成立的是（   ）

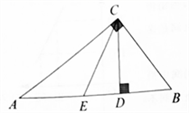
A．    B．    C．    D．

3．如图，在△ABC中，AB＝AC，∠BAC＝50°，∠BAC的角平分线AF与AB的垂直平分线DF交于点F，连接CF，BF，则∠BCF的度数为（　　）

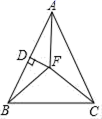
A．30° B．40° C．50° D．45°

4．一次函数，当时，x的取值范围是　　

A． B． C． D．

5．矩形、菱形、正方形都具有的性质是（    ）

A．对角线相等 B．对角线互相平分 C．对角线互相垂直 D．对角线互相平分且相等

6．下列命题的逆命题正确的是（　　）

A．如果两个角都是45°，那么它们相等 B．全等三角形的周长相等

C．同位角相等，两直线平行 D．若a=b，则

7．如图，在△ABC中，∠A=90°，点D在AC边上，DE//BC，若∠1=155°，则∠B的度数为（   ）

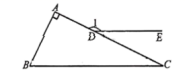
A．55° B．65° C．45° D．75°

8．若一次函数的图像与直线平行，且过点，则此一次函数的解析式为（    ）

A． B． C． D．

9．如图，在中，于点D，且是的中点，若则的长等于（     ）

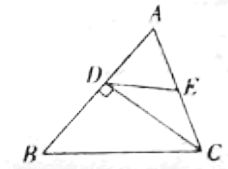
A．5 B．6 C．7 D．8

10．下列方程中有一根为3的是（　　）

A．x2＝3 B．x2﹣4x﹣3＝0

C．x2﹣4x＝﹣3 D．x（x﹣1）＝x﹣3

二、填空题(本大题共有6小题，每小题3分，共18分)

11．如图，已知二次函数y＝ax2+bx+c的图象经过点A（3，0），对称轴为直线x＝1，则点B的坐标是_____．

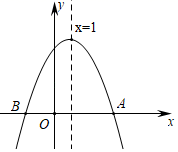
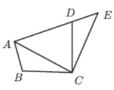
12．如图，是将绕点顺时针旋转得到的．若点，，在同一条直线上，则的度数是______．

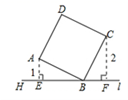
13．如图，直线l过正方形ABCD的顶点B，点A、C到直线l的距离AE、CF分别是1cm、2cm，则线段EF的长为 ______cm．                                                                                                                   

14．函数中，自变量的取值范围是       .

15．分式与的最简公分母是_____．

16．已知二次函数y＝2（x+1）2+1，﹣2≤x≤1，则函数y的最小值是_____，最大值是_____．

三、解下列各题(本大题共8小题，共72分)

17．（8分）先化简：，再从中选取一个合适的代入求值．

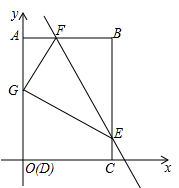
18．（8分）如图，四边形ABCD为矩形，C点在轴上，A点在轴上，D(0，0)，B(3，4)，矩形ABCD沿直线EF折叠，点B落在AD边上的G处，E、F分别在BC、AB边上且F(1，4)．

(1)求G点坐标

(2)求直线EF解析式

(3)点N在坐标轴上，直线EF上是否存在点M，使以M、N、F、G为顶点的四边形是平行四边形？若存在，直接写出M点坐标；若不存在，请说明理由

19．（8分）以四边形ABCD的边AB、AD为边分别向外侧作等边三角形ABF和ADE，连接EB、FD，交点为G．

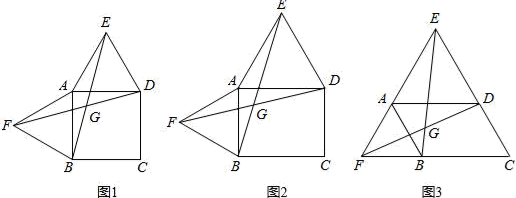
(1)当四边形ABCD为正方形时(如图1)，EB和FD的数量关系是　   　；

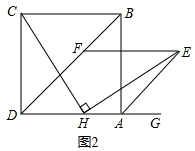
(2)当四边形ABCD为矩形时(如图2)，EB和FD具有怎样的数量关系？请加以证明；

(3)四边形ABCD由正方形到矩形到一般平行四边形的变化过程中，∠EGD是否发生变化？如果改变，请说明理由；如果不变，请在图3中求出∠EGD的度数．

20．（8分）教材第97页在证明“两边对应成比例且夹角对应相等的两个三角形相似”（如图，已知，求证：）时，利用了转化的数学思想，通过添设辅助线，将未知的判定方法转化为前两节课已经解决的方法（即已知两组角对应相等推得相似或已知平行推得相似）．利用上述方法完成这个定理的证明．

21．（8分）第二届全国青年运动会将于2019年8月在太原开幕，这是山西历史上第一次举办全国大型综合性运动会，必将推动我市全民健康理念的提高.某体育用品商店近期购进甲、乙两种运动衫各50件，甲种用了2000元，乙种用了2400元.商店将甲种运动衫的销售单价定为60元，乙种运动衫的销售单价定为88元.该店销售一段时间后发现，甲种运动衫的销售不理想，于是将余下的运动衫按照七折销售；而乙种运动衫的销售价格不变.商店售完这两种运动衫至少可获利2460元，求甲种运动衫按原价销售件数的最小值.

22．（10分）如图1，BD是正方形ABCD的对角线，BC=4，点H是AD边上的一动点，连接CH，作，使得HE=CH，连接AE。

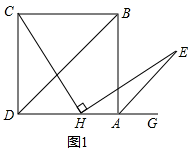
（1）求证：；

（2）如图2，过点E作EF//AD交对角线BD于点F，试探究：在点H的运动过程中，EF的长度是否为一个定值；如果是，请求出EF的长度。

23．（10分）当m，n是正实数，且满足m+n＝mn时，就称点P（m，）为“完美点”．

（1）若点E为完美点，且横坐标为2，则点E的纵坐标为　   　；若点F为完美点，且横坐标为3，则点F的纵坐标为　   　；

（2）完美点P在直线　   　（填直线解析式）上；

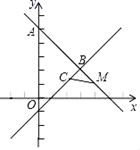
（3）如图，已知点A（0，5）与点M都在直线y＝﹣x+5上，点B，C是“完美点”，且点B在直线AM上．若MC＝，AM＝4，求△MBC的面积．

24．（12分）甲、乙两辆汽车沿同一路线赶赴距出发地480千米的目的地，乙车比甲车晚出发2小时（从甲车出发时开始计时），图中折线OABC、线段DE分别表示甲、乙两车所行路程y（千米）与时间x（小时）之间的函数关系对应的图像线段AB表示甲出发不足2小时因故停车检修），请根据图像所提供的信息，解决如下问题：

（1）求乙车所行路程y与时间x的函数关系式；

（2）求两车在途中第二次相遇时，它们距出发地的路程；

（3）乙车出发多长时间，两车在途中第一次相遇？（写出解题过程）

参考答案

一、选择题(每小题3分,共30分)

1、B

2、C

3、B

4、D

5、B

6、C

7、B

8、D

9、D

10、C

二、填空题(本大题共有6小题，每小题3分，共18分)

11、（﹣1，0）．

12、

13、3

14、．

15、2a-2b

16、1    2   

三、解下列各题(本大题共8小题，共72分)

17、，

18、（1）G（0，4-）；（2）；（3）.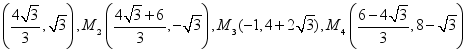

19、（1）EB=FD，（2）EB=FD，证明见解析；（3）不变，等于60°.

20、见解析

21、甲种运动衫按原价销售件数的最小值为20 件.

22、（1）见解析（2）EF为定值4

23、（1）1，2；（2）y＝x﹣1；（3）△MBC的面积=.

24、（1）y=1x﹣120；（2）两车在途中第二次相遇时它们距出发地的路程为240千米；

（3）乙车出发1小时，两车在途中第一次相遇．