黑龙江省密山市实验中学2022-2023学年七年级数学第二学期期末综合测试试题含答案

这是一份黑龙江省密山市实验中学2022-2023学年七年级数学第二学期期末综合测试试题含答案，共7页。试卷主要包含了下列运算正确的是，下列运算,正确的是等内容，欢迎下载使用。
黑龙江省密山市实验中学2022-2023学年七年级数学第二学期期末综合测试试题（时间：120分钟             分数：120分） 学校_______            年级_______        姓名_______ 注意事项1．考试结束后，请将本试卷和答题卡一并交回．2．答题前，请务必将自己的姓名、准考证号用0．5毫米黑色墨水的签字笔填写在试卷及答题卡的规定位置．3．请认真核对监考员在答题卡上所粘贴的条形码上的姓名、准考证号与本人是否相符．4．作答选择题，必须用2B铅笔将答题卡上对应选项的方框涂满、涂黑；如需改动，请用橡皮擦干净后，再选涂其他答案．作答非选择题，必须用05毫米黑色墨水的签字笔在答题卡上的指定位置作答，在其他位置作答一律无效．5．如需作图，须用2B铅笔绘、写清楚，线条、符号等须加黑、加粗． 一、选择题(每小题3分,共30分)1．如图，按下面的程序进行运算．规定：程序运行到“判断结果是否大于35”为一次运算．若运算进行了3次才停止，则x的取值范围是(   )A．7＜x≤11 B．7≤x＜11C．7＜x＜11 D．7≤x≤112．我县某贫围户2016年的家庭年收入为4000元，由于党的扶贫政策的落实，2017、2018年家庭年收入增加到共15000元，设平均每年的增长率为x，可得方程（　　）A．4000（1+x）2=15000 B．4000+4000（1+x）+4000（1+x）2=15000C．4000（1+x）+4000（1+x）2=15000 D．4000+4000（1+x）2=150003．已知：四边形ABCD的对角线AC、BD相交于点O，则下列条件不能判定四边形ABCD是平行四边形的是　　A．， B．，C．， D．，4．要使二次根式有意义，x的值可以是（  ）A．0 B．1 C．2 D．35．若二次根式有意义，则x应满足（　　）A．x≥3 B．x≥﹣3 C．x＞3 D．x＞﹣36．下列运算正确的是（    ）A．＝2 B．＝±2 C． D．7．如图，数轴上点A，B表示的数分别是1，2，过点B作PQ⊥AB，以点B为圆心，AB长为半径画弧，交PQ于点C，以原点O为圆心，OC长为半径画弧，交数轴于点M，则点M表示的数是(　　) A． B．C． D．8．如图所示，线段AC的垂直平分线交线段AB于点D，∠A=40°，则∠BDC=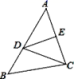（　　）A．40° B．80° C．100° D．120°9．如图，平行四边形ABCD中，E是AB上一点，DE、CE分别是∠ADC、∠BCD的平分线，若AD=5，DE=6，则平行四边形的面积为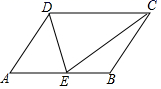（    ）A．96 B．48 C．60 D．3010．下列运算,正确的是(　　)A． B． C． D．二、填空题(本大题共有6小题，每小题3分，共18分)11．如图，在平行四边形中，在上，且，若的面积为3，则四边形的面积为______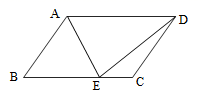．12．在植树节当天，某校一个班同学分成10个小组参加植树造林活动，10个小组植树的株数见下表：植树株数（株）
 5
 6
 7
 小组个数
 3
 4
 3
 则这10个小组植树株数的方差是_____．13．如图，菱形ABCD的边长为4，∠ABC＝60°，且M为BC的中点，P是对角线BD上的一动点，则PM+PC的最小值为_____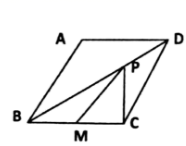．14．若一个多边形的各边都相等，它的周长是63，且它的内角和为900°，则它的边长是________.15．数据 1，2，3，4，5，x 的平均数与众数相等，则 x＝_____．16．不等式组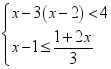的解集为______．三、解下列各题(本大题共8小题，共72分)17．（8分）在平面直角坐标系xOy中，已知一次函数的图象与x轴交于点，与轴交于点． （1）求，两点的坐标；（2）在给定的坐标系中画出该函数的图象；（3）点M（1，y1），N（3，y2）在该函数的图象上，比较y1与y2的大小.   18．（8分）小王开车从甲地到乙地，去时走A线路，全程约100千米，返回时走B路线，全程约60千米.小王开车去时的平均速度比返回时的平均速度快20千米/小时，所用时间却比返回时多15分钟.若小王返回时的平均车速不低于70千米/小时，求小王开车返回时的平均速度.   19．（8分）数学问题：用边长相等的正三角形、正方形和正六边形能否进行平面图形的镶嵌？问题探究：为了解决上述数学问题，我们采用分类讨论的思想方法去进行探究．探究一：从正三角形、正方形和正六边形中任选一种图形，能否进行平面图形的镶嵌？第一类：选正三角形．因为正三角形的每一个内角是60°，所以在镶嵌平面时，围绕某一点有6个正三角形的内角可以拼成一个周角，所以用正三角形可以进行平面图形的镶嵌．第二类：选正方形．因为正方形的每一个内角是90°，所以在镶嵌平面时，围绕某一点有4个正方形的内角可以拼成一个周角，所以用正方形也可以进行平面图形的镶嵌．第三类：选正六边形．(仿照上述方法，写出探究过程及结论)探究二：从正三角形、正方形和正六边形中任选两种图形，能否进行平面图形的镶嵌？第四类：选正三角形和正方形在镶嵌平面时，设围绕某一点有x个正三角形和y个正方形的内角可以拼成个周角．根据题意，可得方程60x+90y＝360整理，得2x+3y＝1．我们可以找到唯一组适合方程的正整数解为.镶嵌平面时，在一个顶点周围围绕着3个正三角形和2个正方形的内角可以拼成一个周角，所以用正三角形和正方形可以进行平面镶嵌第五类：选正三角形和正六边形．(仿照上述方法，写出探究过程及结论)第六类：选正方形和正六边形，(不写探究过程，只写出结论)探究三：用正三角形、正方形和正六边形三种图形是否可以镶嵌平面？第七类：选正三角形、正方形和正六边形三种图形．(不写探究过程，只写结论)，   20．（8分）供电局的电力维修工要到30千米远的郊区进行电力抢修．技术工人骑摩托车先走，15分钟后，抢修车装载着所需材料出发，结果他们同时到达．已知抢修车的速度是摩托车的1.5倍，求这两种车的速度？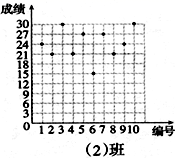   21．（8分）如图，在平面直角坐标系 xOy 中，点 A（0，8），点 B（6，8）．（1）尺规作图：求作一个点 P，使点 P 同时满足下列两个条件（要求保留作图痕迹，不必写出作法）①点 P 到 A，B 两点的距离相等；②点 P 到∠xOy 的两边的距离相等；（2）在（1）作出点 P 后，直接写出点 P 的坐标     ．   22．（10分）如图，以△ABC的三边为边在BC同侧分别作等边三角形，即△ABD，△BCE，△ACF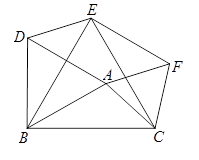．(1)四边形ADEF为__________四边形；(2)当△ABC满足条件____________时，四边形ADEF为矩形；(3)当△ABC满足条件____________时，四边形ADEF为菱形；(4)当△ABC满足条件____________时，四边形ADEF不存在．   23．（10分）王老师为了了解学生在数学学习中常见错误的纠正情况，收集整理了学生在作业和考试中的常见错误，编制了10道选择题，每题3分，对他所教的八年（1）班和八年（2）班进行了检测。如图所示表示从两班随机抽取的10名学生的得分情况：（1）利用图中提供的信息，补全下表：班级平均分（分）中位数（分）众数（分）八年（1）班 2424八年（2）班24  （2）你认为那个班的学生纠错的得分情况比较整齐一些，通过计算说明理由.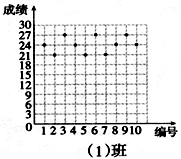       24．（12分）（1）如图①，点 M 是正方形 ABCD 的边 BC 上一点，点 N 是 CD 延长线上一点， 且BM=DN，则线段 AM 与 AN 的关系．（2）如图②，在正方形 ABCD 中，点 E、F分别在边 BC、CD上，且∠EAF=45°，判断 BE，DF，EF 三条线段的数量关系，并说明理由．（3）如图③，在四边形 ABCD中，AB=AD，∠BAD=90°，∠ABC+∠ADC=180°，点E、F分别在边 BC、CD 上，且∠EAF=45°，若 BD=5，EF=3，求四边形 BEFD 的周长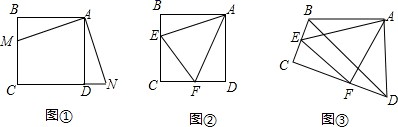．   参考答案 一、选择题(每小题3分,共30分)1、A2、C3、B4、D5、B6、A7、B8、B9、B10、D 二、填空题(本大题共有6小题，每小题3分，共18分)11、912、0.1．13、214、915、316、1＜x≤1 三、解下列各题(本大题共8小题，共72分)17、（1）点A的坐标为， 点B的坐标为 （2）图形见解析（3）  18、80千米/小时19、详见解析20、摩托车的速度是40km/h，抢修车的速度是60km/h．21、（1）见解析；      （2）（3，3）22、 (1)平行；(2)∠BAC=150°；(3)AB=AC且∠BAC≠60°；(4)∠BAC=60°.23、（1）八年（1）班的平均数为24，八年（2）班的中位数为24，众数为21;（2）八年（1）成绩比较整齐.24、（1）结论：AM=AN，AM⊥AN．理由见解析；（2）BE+DF=EF；（3）四边形BEFD的周长为1．