2022-2023学年连云港市重点中学数学七下期末质量检测试题含答案

这是一份2022-2023学年连云港市重点中学数学七下期末质量检测试题含答案，共7页。
2022-2023学年连云港市重点中学数学七下期末质量检测试题（时间：120分钟             分数：120分） 学校_______            年级_______        姓名_______ 注意事项：1．答卷前，考生务必将自己的姓名、准考证号填写在答题卡上。2．回答选择题时，选出每小题答案后，用铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其它答案标号。回答非选择题时，将答案写在答题卡上，写在本试卷上无效。3．考试结束后，将本试卷和答题卡一并交回。 一、选择题(每小题3分,共30分)1．如图，将两块完全相同的矩形纸片ABCD和矩形纸片AEFG按图示方式放置（点A、D、E在同一直线上），连接AC、AF、CF，已知AD＝3，DC＝4，则CF的长是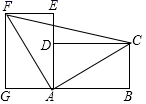（　　）A．5 B．7 C．5 D．102．若方程是一元二次方程，则m的值为（   ）A．0 B．±1 C．1 D．–13．一组数据3、7、2、5、8的中位数是(   ) ．A．2    B．5    C．7    D．84．如图，2002年8月在北京召开的国际数学家大会会徽取材于我国古代数学家赵爽的《勾股圆方图》（也称《赵爽弦图》），它是由四个全等的直角三角形与中间的一个小正方形拼成的一个大正方形，如图所示，如果大正方形的面积是13，小正方形的面积是1，直角三角形的短直角边为a，较长直角边为b，那么的值为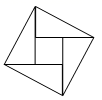（    ）A．13 B．19 C．25 D．1695．如图，在 ABCD中，CD=2AD，BE⊥AD于点E，F为DC的中点，连结EF、BF，下列结论：①∠ABC=2∠ABF；②EF=BF；③S四边形DEBC=2S△EFB；④∠CFE=3∠DEF,其中正确结论的个数共有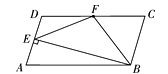（    ）.A．1个 B．2个 C．3个 D．4个6．在ABCD中，AB=3cm，BC=4cm，则ABCD的周长是(   )A．5cm B．7cm C．12cm D．14cm7．将函数的图象向上平移5个单位长度，得到的函数解析式为（  ）A． B．C． D．8．如图，矩形ABCD中，AB=8，BC=1．点E在边AB上，点F在边CD上，点G、H在对角线AC上．若四边形EGFH是菱形，则AE的长是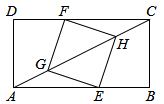（ ）A．2 B．3 C．5 D．69．将抛物线y＝﹣3x2+1向左平移2个单位长度，再向下平移3个单位长度，所得到的抛物线为（　　）A．y＝﹣3（x﹣2）2+4 B．y＝﹣3（x﹣2）2﹣2C．y＝﹣3（x+2）2+4 D．y＝﹣3（x+2）2﹣210．a，b，c为常数，且，则关于x的方程根的情况是　　A．有两个相等的实数根 B．有两个不相等的实数根C．无实数根 D．有一根为0二、填空题(本大题共有6小题，每小题3分，共18分)11．平行四边形ABCD中，∠A－∠B＝20°，则∠A＝______，∠B＝_______.12．＝   ▲   ．13．如图，过点N（0，-1）的直线y=kx+b与图中的四边形ABCD有不少于两个交点，其中A（2，3）、B（1，1）、C（4，1）、D（4，3），则k的取值范围____________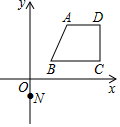14．如图，Rt△ABC中，∠ACB=90°，点D为斜边AB的中点，CD=6cm，则AB的长为      cm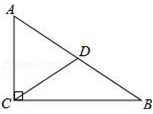．15．已知菱形两条对角线的长分别为12和16，则这个菱形的周长为______.16．在同一平面直角坐标系中，直线与直线的交点不可能在第_______象限 .三、解下列各题(本大题共8小题，共72分)17．（8分）某班级准备购买一些奖品奖励春季运动会表现突出的同学，奖品分为甲、乙两种，已知，购买一个甲奖品比一个乙奖品多用20元，若用400元购买甲奖品的个数是用160元购买乙奖品个数的一半.（1）求购买一个甲奖品和一个乙奖品各需多少元？（2）经商谈，商店决定给予该班级每购买甲奖品3个就赠送一个乙奖品的优惠，如果该班级需要乙奖品的个数是甲奖品的2倍还多8个，且该班级购买两种奖项的总费用不超过640元，那么该班级最多可购买多少个甲奖品？   18．（8分）一次期中考试中，甲、乙、丙、丁、戍五位同学的数学、英语成绩等有关信息如下 表所示：（单位：分） 甲乙丙丁戍平均分标准差数学7172696870 英语888294857685 （1）求这五位同学在本次考试中数学成绩的平均分和英语成绩的标准差；（2）为了比较不同学科考试成绩的好与差，采用标准分是一个合理的选择．标准分 的计算公式是：标准分＝（个人成绩－平均成绩）÷成绩标准差．从标准分看， 标准分大的考试成绩更好．请问甲同学在本次考试中，数学与英语哪个学科考 得更好？   19．（8分）已知，如图，在平行四边形ABCD中，AC、BD相交于O点，点E、F分别为BO、DO的中点，连接AF，CE．（1）求证：四边形AECF是平行四边形；（2）如果E，F点分别在DB和BD的延长线上时，且满足BE=DF，上述结论仍然成立吗？请说明理由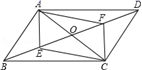．   20．（8分）某学习小组在学习了函数及函数图象的知识后，想利用此知识来探究周长一定的矩形其边长分别为多少时面积最大. 请将他们的探究过程补充完整.（1）列函数表达式：若矩形的周长为8，设矩形的一边长为x，面积为y，则有y=____________；（2）上述函数表达式中，自变量x的取值范围是____________；（3）列表：x…0.511.522.533.5…y…1.7533.7543.753m… 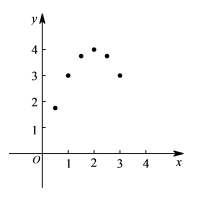        写出m=____________；（4）画图：在平面直角坐标系中已描出了上表中部分各对应值为坐标的点，请你画出该函数的图象；（5）结合图象可得，x=____________时，矩形的面积最大；写出该函数的其它性质（一条即可）：____________.   21．（8分）某学校需要置换一批推拉式黑板，经了解，现有甲、乙两厂家报价均为100元/米1，且提供的售后服务完全相同，为了促销，甲厂家表示，每平方米都按七折计费；乙厂家表示，如果黑板总面积不超过10米1，每平方米都按九折计费，超过10米1，那么超出部分每平方米按六折计费．假设学校需要置换的黑板总面积为x米1．            （1）请分别写出甲、乙两厂家收取的总费用y（元）与x（米1）之间的函数关系式；    （1）请你结合函数图象的知识帮助学校在甲、乙两厂家中，选择一家收取总费用较少的．   22．（10分）如图，直线y＝x＋9分别交x轴、y轴于点A、B，∠ABO的平分线交x轴于点C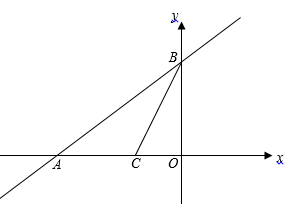．（1）求点A、B、C的坐标；（2）若点M与点A、B、C是平行四边形的四个顶点，求CM所在直线的解析式．   23．（10分）已知关于x的方程 (m-1)x-mx+1=0。（1）证明：不论m为何值时，方程总有实数根；（2）若m为整数，当m为何值时，方程有两个不相等的整数根。   24．（12分）孝感市委市政府为了贯彻落实国家的“精准扶贫”战略部署，组织相关企业开展扶贫工作，博大公司为此制定了关于帮扶A、B两贫困村的计划．今年3月份决定从某地运送152箱鱼苗到A、B两村养殖，若用大小货车共15辆，则恰好能一次性运完这批鱼苗．已知这两种大小货车的载货能力分别为12箱/辆和8箱/辆，其运往A、B两村的运费如表：目的地费用车型A村（元/辆）B村（元/辆）大货车800900小货车400600（1）求这15辆车中大小货车各多少辆？（2）现安排其中10辆货车前往A村，其余货车前往B村，设前往A村的大货车为x辆，前往A、B两村总运费为y元；①试求出y与x的函数解析式；②若运往A村的鱼苗不少于108箱，请你写出使总运费最少的货车调配方案，并求出最少运费．   参考答案 一、选择题(每小题3分,共30分)1、C2、D3、B4、C5、D6、D7、A8、C9、D10、B 二、填空题(本大题共有6小题，每小题3分，共18分)11、100°，    80°    12、1．13、＜k≤2．14、1.15、116、四 三、解下列各题(本大题共8小题，共72分)17、（1）购买一个甲奖品需元，买一个乙奖品需要元；（2）该班级最多可购买个甲奖品.18、（1）70，6；（2）从标准分来看，甲同学数学比英语考得更好.19、见解析20、见解析21、（1）甲厂家的总费用：y甲=140x；乙厂家的总费用：当0＜x≤10时，y乙=180x，当x＞10时，y乙=110x+1100；（1）详见解析.22、（1）；（2）或23、（1）见解析；（2）m=024、（1）这15辆车中大货车用8辆，小货车用7辆；（2）①y＝100x+9400（3≤x≤8，且x为整数）；②使总运费最少的调配方案是：7辆大货车、3辆小货车前往A村；1辆大货车、4辆小货车前往B村．最少运费为10100元．