


2022-2023学年辽宁省锦州黑山县数学七下期末检测试题含答案
展开
这是一份2022-2023学年辽宁省锦州黑山县数学七下期末检测试题含答案,共7页。试卷主要包含了考生要认真填写考场号和座位序号,函数y=中,自变量的取值范围是,下列说法中,错误的是等内容,欢迎下载使用。
2022-2023学年辽宁省锦州黑山县数学七下期末检测试题(时间:120分钟 分数:120分) 学校_______ 年级_______ 姓名_______ 注意事项1.考生要认真填写考场号和座位序号。2.试题所有答案必须填涂或书写在答题卡上,在试卷上作答无效。第一部分必须用2B 铅笔作答;第二部分必须用黑色字迹的签字笔作答。3.考试结束后,考生须将试卷和答题卡放在桌面上,待监考员收回。 一、选择题(每小题3分,共30分)1.直角三角形斜边上的高与中线分别为 5cm 和 6cm,则它的面积为( )cm1.A.30 B.60 C.45 D.152.以下各点中,在一次函数![]() 的图像上的是( )A.(2,4) B.(-1,4) C.(0,5) D.(0,6)3.下列各曲线中不能表示y是x函数的是( )A.
的图像上的是( )A.(2,4) B.(-1,4) C.(0,5) D.(0,6)3.下列各曲线中不能表示y是x函数的是( )A.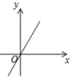 B.
B.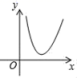 C.
C.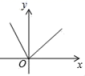 D.
D.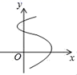 4.如图,在正方形
4.如图,在正方形![]() 外取一点
外取一点![]() ,连接
,连接![]() 、
、![]() 、
、![]() ,过点
,过点![]() 作
作![]() 的垂线交
的垂线交![]() 于点
于点![]() .若
.若![]() ,
,![]() ,下列结论:①
,下列结论:①![]() ;②
;②![]() ;③点
;③点![]() 到直线
到直线![]() 的距离为
的距离为![]() ;④
;④![]() ;⑤
;⑤![]() 正方形
正方形![]() .其中正确的是( )
.其中正确的是( )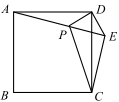 A.①②③④ B.①②④⑤ C.①③④ D.①②⑤5.如图,在
A.①②③④ B.①②④⑤ C.①③④ D.①②⑤5.如图,在![]() ABCD中,AC与BD相交于点O,则下列结论不一定成立的是( )
ABCD中,AC与BD相交于点O,则下列结论不一定成立的是( )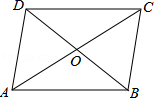 A.BO=DO B.CD=AB C.∠BAD=∠BCD D.AC=BD6.用一些相同的正方形,摆成如下的一些大正方形,如图第(1)个图中小正方形只有一个,且阴影面积为1,第(2)个图中阴影小正方形面积和3;第(3)个图中阴影小正方形面积和为5,第(9)个图中阴影小正方形面积和为( )
A.BO=DO B.CD=AB C.∠BAD=∠BCD D.AC=BD6.用一些相同的正方形,摆成如下的一些大正方形,如图第(1)个图中小正方形只有一个,且阴影面积为1,第(2)个图中阴影小正方形面积和3;第(3)个图中阴影小正方形面积和为5,第(9)个图中阴影小正方形面积和为( )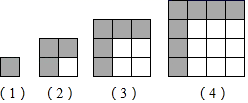 A.11 B.13 C.15 D.177.一次函数y=﹣2x+1的图象不经过( )A.第一象限 B.第二象限 C.第三象限 D.第四象限8.某天小明骑自行车上学,途中因自行车发生故障,修车耽误了一段时间后继续骑行,按时赶到了学校.如图描述了他上学的情景,下列说法中错误的是( )
A.11 B.13 C.15 D.177.一次函数y=﹣2x+1的图象不经过( )A.第一象限 B.第二象限 C.第三象限 D.第四象限8.某天小明骑自行车上学,途中因自行车发生故障,修车耽误了一段时间后继续骑行,按时赶到了学校.如图描述了他上学的情景,下列说法中错误的是( )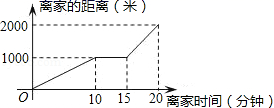 A.自行车发生故障时离家距离为1000米B.学校离家的距离为2000米C.到达学校时共用时间20分钟D.修车时间为15分钟9.函数y=
A.自行车发生故障时离家距离为1000米B.学校离家的距离为2000米C.到达学校时共用时间20分钟D.修车时间为15分钟9.函数y=![]() 中,自变量
中,自变量![]() 的取值范围是( ).A.
的取值范围是( ).A.![]() B.
B.![]() C.
C.![]() 且
且![]() D.
D.![]() 10.下列说法中,错误的是( )A.平行四边形的对角线互相平分 B.菱形的对角线互相垂直C.矩形的对角线相等 D.正方形的对角线不一定互相平分二、填空题(本大题共有6小题,每小题3分,共18分)11.如图所示,△ABC中,CD⊥AB于D,E是AC的中点,若DE=5,则AC的长等于_____.
10.下列说法中,错误的是( )A.平行四边形的对角线互相平分 B.菱形的对角线互相垂直C.矩形的对角线相等 D.正方形的对角线不一定互相平分二、填空题(本大题共有6小题,每小题3分,共18分)11.如图所示,△ABC中,CD⊥AB于D,E是AC的中点,若DE=5,则AC的长等于_____.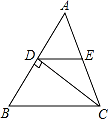 12.如图,公路
12.如图,公路![]() 互相垂直,公路
互相垂直,公路![]() 的中点
的中点![]() 与点
与点![]() 被湖隔开,若测得
被湖隔开,若测得![]() 的长为2.4km,则
的长为2.4km,则![]() 两点间的距离为______km.
两点间的距离为______km.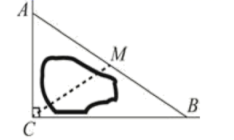 13.如图,在
13.如图,在![]() 中,
中,![]() ,将
,将![]() 绕顶点
绕顶点![]() 顺时针旋转,旋转角为
顺时针旋转,旋转角为![]() ,得到
,得到![]() .设
.设![]() 中点为
中点为![]() ,
,![]() 中点为
中点为![]() ,
,![]() ,连接
,连接![]() ,当
,当![]() ____________
____________![]() 时,
时,![]() 长度最大,最大值为____________.
长度最大,最大值为____________.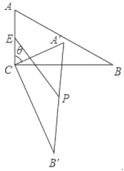 14.若对于
14.若对于![]() 的任何值,等式
的任何值,等式![]() 恒成立,则
恒成立,则![]() __________.15.如图,在平面直角坐标系
__________.15.如图,在平面直角坐标系![]() 中,点
中,点![]() ,射线
,射线![]() 轴,直线
轴,直线![]() 交线段
交线段![]() 于点
于点![]() ,交
,交![]() 轴于点
轴于点![]() ,
,![]() 是射线
是射线![]() 上一点.若存在点
上一点.若存在点![]() ,使得
,使得![]() 恰为等腰直角三角形,则
恰为等腰直角三角形,则![]() 的值为_______.
的值为_______.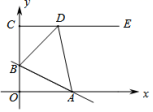 16.点A(-1,y1),B(3,y2)是直线y=-4x+3图象上的两点,则y1______y2(填“>”或“<”).三、解下列各题(本大题共8小题,共72分)17.(8分)图1,抛物线与x轴交于A(﹣1,0),B(3,0),顶点为D(1,﹣4),点P为y轴上一动点.(1)求抛物线的解析式;(2)在y轴的负半轴上是否存在点P,使△BDP是等腰三角形?若存在,求出点P的坐标;若不存在,请说明理由.(3)如图2,点
16.点A(-1,y1),B(3,y2)是直线y=-4x+3图象上的两点,则y1______y2(填“>”或“<”).三、解下列各题(本大题共8小题,共72分)17.(8分)图1,抛物线与x轴交于A(﹣1,0),B(3,0),顶点为D(1,﹣4),点P为y轴上一动点.(1)求抛物线的解析式;(2)在y轴的负半轴上是否存在点P,使△BDP是等腰三角形?若存在,求出点P的坐标;若不存在,请说明理由.(3)如图2,点![]() 在抛物线上,求
在抛物线上,求![]() 的最小值.
的最小值.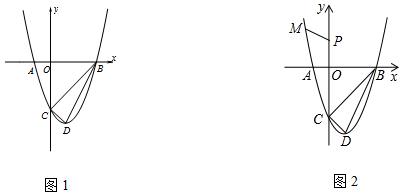 18.(8分)如图,在△ABC 中,AB=AC,∠BAC=120°,E 为 BC 上一点,以 CE 为直径作⊙O 恰好经过 A、C 两点, PF⊥BC 交 BC 于点 G,交 AC 于点 F.(1)求证:AB 是⊙O 的切线;(2)如果 CF =2,CP =3,求⊙O 的直径 EC.
18.(8分)如图,在△ABC 中,AB=AC,∠BAC=120°,E 为 BC 上一点,以 CE 为直径作⊙O 恰好经过 A、C 两点, PF⊥BC 交 BC 于点 G,交 AC 于点 F.(1)求证:AB 是⊙O 的切线;(2)如果 CF =2,CP =3,求⊙O 的直径 EC.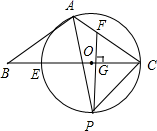 19.(8分)现有正方形ABCD和一个以O为直角顶点的三角板,移动三角板,使三角板两直角边所在直线分别与直线BC、CD交于点M、N.(1)如图1,若点O与点A重合,则OM与ON的数量关系是 ;(2)如图2,若点O在正方形的中心(即两对角线交点),则(1)中的结论是否仍然成立?请说明理由;(3)如图3,若点O在正方形的内部(含边界),当OM=ON时,请探究点O在移动过程中可形成什么图形?(4)如图4,是点O在正方形外部的一种情况.当OM=ON时,请你就“点O的位置在各种情况下(含外部)移动所形成的图形”提出一个正确的结论.(不必说明)
19.(8分)现有正方形ABCD和一个以O为直角顶点的三角板,移动三角板,使三角板两直角边所在直线分别与直线BC、CD交于点M、N.(1)如图1,若点O与点A重合,则OM与ON的数量关系是 ;(2)如图2,若点O在正方形的中心(即两对角线交点),则(1)中的结论是否仍然成立?请说明理由;(3)如图3,若点O在正方形的内部(含边界),当OM=ON时,请探究点O在移动过程中可形成什么图形?(4)如图4,是点O在正方形外部的一种情况.当OM=ON时,请你就“点O的位置在各种情况下(含外部)移动所形成的图形”提出一个正确的结论.(不必说明) 20.(8分)已知:如图,已知直线AB的函数解析式为
20.(8分)已知:如图,已知直线AB的函数解析式为 ![]() ,AB与y轴交于点 ,与x轴交于点 .(1)在答题卡上直接写出A,B两点的坐标;(2)若点P(a,b)为线段AB上的一个动点,作PE⊥y轴于点E,PF⊥x轴于点 F,连接EF.问:①若
,AB与y轴交于点 ,与x轴交于点 .(1)在答题卡上直接写出A,B两点的坐标;(2)若点P(a,b)为线段AB上的一个动点,作PE⊥y轴于点E,PF⊥x轴于点 F,连接EF.问:①若![]() 的面积为 S,求S关于a的函数关系式;② 是否存在点P,使EF的值最小?若存在,求出EF的最小值;若不存在,请说明理由.
的面积为 S,求S关于a的函数关系式;② 是否存在点P,使EF的值最小?若存在,求出EF的最小值;若不存在,请说明理由.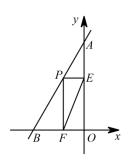 21.(8分)某产品生产车间有工人10名.已知每名工人每天可生产甲种产品12个或乙种产品10个,且每生产一个甲种产品可获利润100元,每生产一个乙种产品可获利润180元.在这10名工人中,如果要使此车间每天所获利润不低于15600元,你认为至少要派多少名工人去生产乙种产品才合适. 22.(10分)已知正比例函数y=kx经过点A,点A在第四象限,过点A作AH⊥x轴,垂足为点H,点A的横坐标为1,且△AOH的面积为1.(1)求正比例函数的解析式;(2)在x轴上能否找到一点P,使△AOP的面积为5?若存在,求点P的坐标;若不存在,请说明理由.
21.(8分)某产品生产车间有工人10名.已知每名工人每天可生产甲种产品12个或乙种产品10个,且每生产一个甲种产品可获利润100元,每生产一个乙种产品可获利润180元.在这10名工人中,如果要使此车间每天所获利润不低于15600元,你认为至少要派多少名工人去生产乙种产品才合适. 22.(10分)已知正比例函数y=kx经过点A,点A在第四象限,过点A作AH⊥x轴,垂足为点H,点A的横坐标为1,且△AOH的面积为1.(1)求正比例函数的解析式;(2)在x轴上能否找到一点P,使△AOP的面积为5?若存在,求点P的坐标;若不存在,请说明理由.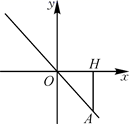 23.(10分)如图所示,四边形ABCD是平行四边形,已知DE平分∠ADC,交AB于点E,过点E作EF∥AD,交DC于F,求证:四边形AEFD是菱形.
23.(10分)如图所示,四边形ABCD是平行四边形,已知DE平分∠ADC,交AB于点E,过点E作EF∥AD,交DC于F,求证:四边形AEFD是菱形.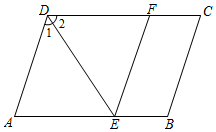 24.(12分)如图,为修通铁路凿通隧道
24.(12分)如图,为修通铁路凿通隧道![]() ,量出
,量出![]() ,
,![]() ,
,![]() ,
,![]() ,若每天凿隧道
,若每天凿隧道![]() ,问几天才能把隧道
,问几天才能把隧道![]() 凿通?
凿通?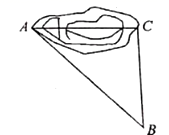 参考答案 一、选择题(每小题3分,共30分)1、A2、D3、D4、D5、D6、D7、C8、D9、D10、D 二、填空题(本大题共有6小题,每小题3分,共18分)11、112、1.113、
参考答案 一、选择题(每小题3分,共30分)1、A2、D3、D4、D5、D6、D7、C8、D9、D10、D 二、填空题(本大题共有6小题,每小题3分,共18分)11、112、1.113、![]() 3 14、
3 14、![]() 15、3或616、y1>y2 三、解下列各题(本大题共8小题,共72分)17、(1)y=x1﹣1x﹣3;(1)点P坐标为(0,﹣
15、3或616、y1>y2 三、解下列各题(本大题共8小题,共72分)17、(1)y=x1﹣1x﹣3;(1)点P坐标为(0,﹣![]() )或(0,﹣
)或(0,﹣![]() ﹣4)或(0,﹣1);(3)
﹣4)或(0,﹣1);(3)![]() 18、(1)见解析;(2)⊙O 的直径EC= 1
18、(1)见解析;(2)⊙O 的直径EC= 1![]() .19、(1)OM=ON;(2)成立.(3)O在移动过程中可形成线段AC;(4)O在移动过程中可形成线段AC.20、(1)
.19、(1)OM=ON;(2)成立.(3)O在移动过程中可形成线段AC;(4)O在移动过程中可形成线段AC.20、(1)![]() ;(2)①
;(2)①![]() (-5≤a≤0); ②存在,
(-5≤a≤0); ②存在,![]() 21、6名.22、(1)y=-
21、6名.22、(1)y=-![]() x;(2)点P的坐标为(5,0)或(﹣5,0).23、详见解析.24、10天才能把隧道
x;(2)点P的坐标为(5,0)或(﹣5,0).23、详见解析.24、10天才能把隧道![]() 凿通
凿通
相关试卷
这是一份辽宁省锦州黑山县2023-2024学年数学九上期末监测试题含答案,共8页。试卷主要包含了若反比例函数的图象经过点,-2019的相反数是等内容,欢迎下载使用。
这是一份辽宁省锦州黑山县2023-2024学年数学八上期末考试试题含答案,共6页。试卷主要包含了答题时请按要求用笔,若分式的值为零,则的值为,分式方程的解是,下列命题是真命题的是等内容,欢迎下载使用。
这是一份辽宁省锦州黑山县2023-2024学年八年级数学第一学期期末检测模拟试题含答案,共7页。试卷主要包含了计算的平方根为,如果,且,那么点在等内容,欢迎下载使用。









