


2022-2023学年重庆合川区南屏中学数学七下期末质量检测模拟试题含答案
展开
这是一份2022-2023学年重庆合川区南屏中学数学七下期末质量检测模拟试题含答案,共7页。试卷主要包含了答题时请按要求用笔,使分式有意义的的取值范围是等内容,欢迎下载使用。
2022-2023学年重庆合川区南屏中学数学七下期末质量检测模拟试题(时间:120分钟 分数:120分) 学校_______ 年级_______ 姓名_______ 注意事项:1.答题前,考生先将自己的姓名、准考证号码填写清楚,将条形码准确粘贴在条形码区域内。2.答题时请按要求用笔。3.请按照题号顺序在答题卡各题目的答题区域内作答,超出答题区域书写的答案无效;在草稿纸、试卷上答题无效。4.作图可先使用铅笔画出,确定后必须用黑色字迹的签字笔描黑。5.保持卡面清洁,不要折暴、不要弄破、弄皱,不准使用涂改液、修正带、刮纸刀。 一、选择题(每小题3分,共30分)1.如图,某工厂有甲、乙两个大小相同的蓄水池,且中间有管道连通,现要向甲池中注水,若单位时间内的注水量不变,那么从注水开始,乙水池水面上升的高度h与注水时间t之间的函数关系图象可能是( )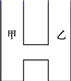 A.
A.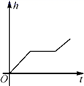 B.
B.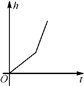 C.
C.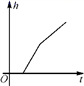 D.
D.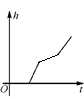 2.下列各点中在函数y=2x+2的图象上的是( )A.(1,-2) B.(-1,-1) C.(0,2) D.(2,0)3.一个容量为80的样本最大值为143,最小值为50,取组距为10,则可以分成( )A.10组 B.9组 C.8组 D.7组4.不等式组
2.下列各点中在函数y=2x+2的图象上的是( )A.(1,-2) B.(-1,-1) C.(0,2) D.(2,0)3.一个容量为80的样本最大值为143,最小值为50,取组距为10,则可以分成( )A.10组 B.9组 C.8组 D.7组4.不等式组![]() 的正整数解的个数有( )A.1个 B.2个 C.3个 D.4个5.矩形、菱形、正方形都具有的性质是( )A.对角线互相垂直B.对角线互相平分C.对角线相等D.每一条对角线平分一组对角6.目前我国已建立了比较完善的经济困难学生资助体系,某校去年上半年发放给每个经济困难学生389元,今年上半年发放了438元.设每半年发放的资助金额的平均增长率为x,则下面列出的方程中正确的是( )A.438(1+x)2=389 B.389(1+x)2=438C.389(1+2x)=438 D.438(1+2x)=3897.直角三角形斜边上的高与中线分别为 5cm 和 6cm,则它的面积为( )cm1.A.30 B.60 C.45 D.158.将一副三角尺按如图的方式摆放,其中l1∥l2,则∠α的度数是( )
的正整数解的个数有( )A.1个 B.2个 C.3个 D.4个5.矩形、菱形、正方形都具有的性质是( )A.对角线互相垂直B.对角线互相平分C.对角线相等D.每一条对角线平分一组对角6.目前我国已建立了比较完善的经济困难学生资助体系,某校去年上半年发放给每个经济困难学生389元,今年上半年发放了438元.设每半年发放的资助金额的平均增长率为x,则下面列出的方程中正确的是( )A.438(1+x)2=389 B.389(1+x)2=438C.389(1+2x)=438 D.438(1+2x)=3897.直角三角形斜边上的高与中线分别为 5cm 和 6cm,则它的面积为( )cm1.A.30 B.60 C.45 D.158.将一副三角尺按如图的方式摆放,其中l1∥l2,则∠α的度数是( )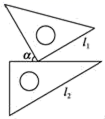 A.30° B.45° C.60° D.70°9.将100个数据分成①-⑧组,如下表所示:组号①②③④⑤⑥⑦⑧频数4812 241873那么第④组的频率为( )A.0.24 B.0.26 C.24 D.2610.使分式
A.30° B.45° C.60° D.70°9.将100个数据分成①-⑧组,如下表所示:组号①②③④⑤⑥⑦⑧频数4812 241873那么第④组的频率为( )A.0.24 B.0.26 C.24 D.2610.使分式![]() 有意义的
有意义的![]() 的取值范围是( )A.
的取值范围是( )A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 二、填空题(本大题共有6小题,每小题3分,共18分)11.某班七个兴趣小组人数分别为4,x,5,5,4,6,7,已知这组数据的平均数是5,则x=________.12.有一组数据如下:2,3,a,5,6,它们的平均数是4,则这组数据的方差是 .13.菱形ABCD的两条对角线长分别为6cm和8cm,则菱形ABCD的面积为_____;周长为______.14.如图,在矩形ABCD中,AB=5,AD=9,点P为AD边上点,沿BP折叠△ABP,点A的对应点为E,若点E到矩形两条较长边的距离之比为1:4,则AP的长为_____.
二、填空题(本大题共有6小题,每小题3分,共18分)11.某班七个兴趣小组人数分别为4,x,5,5,4,6,7,已知这组数据的平均数是5,则x=________.12.有一组数据如下:2,3,a,5,6,它们的平均数是4,则这组数据的方差是 .13.菱形ABCD的两条对角线长分别为6cm和8cm,则菱形ABCD的面积为_____;周长为______.14.如图,在矩形ABCD中,AB=5,AD=9,点P为AD边上点,沿BP折叠△ABP,点A的对应点为E,若点E到矩形两条较长边的距离之比为1:4,则AP的长为_____. 15.在平面直角坐标系中,已知一次函数y=
15.在平面直角坐标系中,已知一次函数y=![]() x+1的图象经过P1(x1,y1)、P2(x2,y2)两点,若x1<x2,则y1_____y2(填“>”,“<”或“=”).16.如图,所有阴影部分四边形都是正方形,所有三角形都是直角三角形,若正方形B、C、D的面积依次为4、3、9,则正方形A的面积为_______.
x+1的图象经过P1(x1,y1)、P2(x2,y2)两点,若x1<x2,则y1_____y2(填“>”,“<”或“=”).16.如图,所有阴影部分四边形都是正方形,所有三角形都是直角三角形,若正方形B、C、D的面积依次为4、3、9,则正方形A的面积为_______.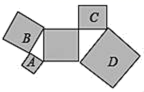 三、解下列各题(本大题共8小题,共72分)17.(8分)在我国古代数学著作《九章算术》中记载了一道有趣的数学问题:“今有池方一丈,葭生其中央,出水一尺.引葭赴岸,适与岸齐.问水深几何?”这个数学问题的意思是说:“有一个水池,水面是一个边长为1丈(1丈=10尺)的正方形,在水池正中央长有一根芦苇,芦苇露出水面1尺.如果把这根芦苇拉向岸边,它的顶端恰好到达岸边的水面,请问这个水池深多少尺?”
三、解下列各题(本大题共8小题,共72分)17.(8分)在我国古代数学著作《九章算术》中记载了一道有趣的数学问题:“今有池方一丈,葭生其中央,出水一尺.引葭赴岸,适与岸齐.问水深几何?”这个数学问题的意思是说:“有一个水池,水面是一个边长为1丈(1丈=10尺)的正方形,在水池正中央长有一根芦苇,芦苇露出水面1尺.如果把这根芦苇拉向岸边,它的顶端恰好到达岸边的水面,请问这个水池深多少尺?”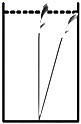 18.(8分)如图,在□ABCD中,∠ABC,∠BCD的平分线分别交AD于点E,F,BE,CF相交于点G.(1)求证:BE⊥CF;(2)若AB=a,CF=b,写出求BE的长的思路.
18.(8分)如图,在□ABCD中,∠ABC,∠BCD的平分线分别交AD于点E,F,BE,CF相交于点G.(1)求证:BE⊥CF;(2)若AB=a,CF=b,写出求BE的长的思路.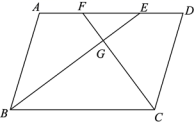 19.(8分)如图,在边长为1的小正方形网格中,△AOB的顶点均在格点上,(1)将△AOB向右平移4个单位长度得到△A1O1B1,请画出△A1O1B1;(2)以点A为对称中心,请画出△ AOB关于点A成中心对称的△ A O2 B2,并写点B2的坐标;(1)以原点O为旋转中心,请画出把△AOB按顺时针旋转90°的图形△A2 O B1.
19.(8分)如图,在边长为1的小正方形网格中,△AOB的顶点均在格点上,(1)将△AOB向右平移4个单位长度得到△A1O1B1,请画出△A1O1B1;(2)以点A为对称中心,请画出△ AOB关于点A成中心对称的△ A O2 B2,并写点B2的坐标;(1)以原点O为旋转中心,请画出把△AOB按顺时针旋转90°的图形△A2 O B1.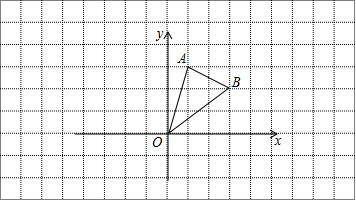 20.(8分)如图,平行四边形ABCD中,AC、BD相交于点O,若AD=6,AC+BD=16,求△BOC的周长为多大?
20.(8分)如图,平行四边形ABCD中,AC、BD相交于点O,若AD=6,AC+BD=16,求△BOC的周长为多大?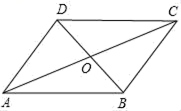 21.(8分)如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(﹣4,3),B(﹣3,1),C(﹣1,3).(1)请按下列要求画图:①平移△ABC,使点A的对应点A1的坐标为(﹣4,﹣3),请画出平移后的△A1B1C1;②△A1B1C1与△ABC关于原点O中心对称,画出△A1B1C1.(1)若将△A1B1C1绕点M旋转可得到△A1B1C1,请直接写出旋转中心M点的坐标 .
21.(8分)如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(﹣4,3),B(﹣3,1),C(﹣1,3).(1)请按下列要求画图:①平移△ABC,使点A的对应点A1的坐标为(﹣4,﹣3),请画出平移后的△A1B1C1;②△A1B1C1与△ABC关于原点O中心对称,画出△A1B1C1.(1)若将△A1B1C1绕点M旋转可得到△A1B1C1,请直接写出旋转中心M点的坐标 .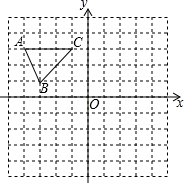 22.(10分)某房地产开发公司计划建A、B两种户型的住房共80套,该公司所筹资金不少于2090万元,但不超过2096万元,且所筹资金全部用于建房,两种户型的建房成本和售价如下表: AB成本(万元/套)2528售价(万元/套)3034(1)该公司对这两种户型住房有哪几种建房方案?(2)该公司如何建房获得利润最大?(3)根据市场调查,每套B型住房的售价不会改变,每套A型住房的售价将会提高a万元(a>0),且所建的两种住房可全部售出,该公司又将如何建房获得利润最大?(注:利润=售价-成本) 23.(10分)如图1,已知△ABC,AB=AC,以边AB为直径的⊙O交BC于点D,交AC于点E,连接DE.
22.(10分)某房地产开发公司计划建A、B两种户型的住房共80套,该公司所筹资金不少于2090万元,但不超过2096万元,且所筹资金全部用于建房,两种户型的建房成本和售价如下表: AB成本(万元/套)2528售价(万元/套)3034(1)该公司对这两种户型住房有哪几种建房方案?(2)该公司如何建房获得利润最大?(3)根据市场调查,每套B型住房的售价不会改变,每套A型住房的售价将会提高a万元(a>0),且所建的两种住房可全部售出,该公司又将如何建房获得利润最大?(注:利润=售价-成本) 23.(10分)如图1,已知△ABC,AB=AC,以边AB为直径的⊙O交BC于点D,交AC于点E,连接DE.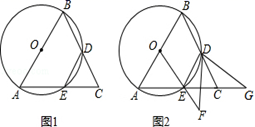 (1)求证:DE=DC.(2)如图2,连接OE,将∠EDC绕点D逆时针旋转,使∠EDC的两边分别交OE的延长线于点F,AC的延长线于点G.试探究线段DF、DG的数量关系. 24.(12分)在Rt△ABC中,∠BAC=90°,D是BC的中点,E是AD的中点,过点A作AF∥BC交BE的延长线于点F,连接CF.(1)求证:AF=BD.(2)求证:四边形ADCF是菱形.
(1)求证:DE=DC.(2)如图2,连接OE,将∠EDC绕点D逆时针旋转,使∠EDC的两边分别交OE的延长线于点F,AC的延长线于点G.试探究线段DF、DG的数量关系. 24.(12分)在Rt△ABC中,∠BAC=90°,D是BC的中点,E是AD的中点,过点A作AF∥BC交BE的延长线于点F,连接CF.(1)求证:AF=BD.(2)求证:四边形ADCF是菱形.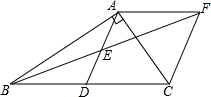 参考答案 一、选择题(每小题3分,共30分)1、D2、C3、A4、C5、B6、B7、A8、C9、A10、A 二、填空题(本大题共有6小题,每小题3分,共18分)11、412、113、24 cm2 20 cm 14、
参考答案 一、选择题(每小题3分,共30分)1、D2、C3、A4、C5、B6、B7、A8、C9、A10、A 二、填空题(本大题共有6小题,每小题3分,共18分)11、412、113、24 cm2 20 cm 14、![]() 15、
15、![]() 16、1 三、解下列各题(本大题共8小题,共72分)17、1尺18、 (1)见解析;(2)见解析.19、(1)如图所示:△A1O1B1为所求作的三角形;见解析;(2)如图所示:
16、1 三、解下列各题(本大题共8小题,共72分)17、1尺18、 (1)见解析;(2)见解析.19、(1)如图所示:△A1O1B1为所求作的三角形;见解析;(2)如图所示:![]() 为所求作的三角形,见解析;
为所求作的三角形,见解析;![]() (-1,4);(1)如图所示:
(-1,4);(1)如图所示:![]() 为所求作的三角形;见解析.20、121、(1)①见解析②见解析(1)(0,﹣3)22、(1)三种建房方案(2)A型住房48套,B型住房32套获得利润最大(3)当O<a<l时, x=48,W最大,当a=l时,a-1=O,三种建房方案获得利润相等,当a>1时,x=1,W最大.23、(1)证明见试题解析;(2)DF=DG.24、(1)见解析;(2)见解析.
为所求作的三角形;见解析.20、121、(1)①见解析②见解析(1)(0,﹣3)22、(1)三种建房方案(2)A型住房48套,B型住房32套获得利润最大(3)当O<a<l时, x=48,W最大,当a=l时,a-1=O,三种建房方案获得利润相等,当a>1时,x=1,W最大.23、(1)证明见试题解析;(2)DF=DG.24、(1)见解析;(2)见解析.
相关试卷
这是一份2023-2024学年江西省上饶市广丰区丰溪街道南屏中学数学九年级第一学期期末质量检测模拟试题含答案,共9页。
这是一份重庆合川区南屏中学2023-2024学年数学八上期末质量跟踪监视模拟试题含答案,共6页。试卷主要包含了下列命题,是真命题的是,数字用科学记数法表示为,下列表述中,能确定准确位置的是等内容,欢迎下载使用。
这是一份2023-2024学年重庆合川区凉亭中学数学八上期末考试试题含答案,共7页。试卷主要包含了数字用科学记数法表示为,下列命题中是真命题的是,下列计算正确的是,若方程无解,则的值为等内容,欢迎下载使用。









