2022-2023学年重庆市南川中学七年级数学第二学期期末监测模拟试题含答案

这是一份2022-2023学年重庆市南川中学七年级数学第二学期期末监测模拟试题含答案，共6页。试卷主要包含了答题时请按要求用笔，下面调查中，适合采用普查的是，甲、乙两车从A城出发前往B城，若分式有意义，则的取值范围是等内容，欢迎下载使用。
2022-2023学年重庆市南川中学七年级数学第二学期期末监测模拟试题（时间：120分钟             分数：120分） 学校_______            年级_______        姓名_______ 注意事项:1．答题前，考生先将自己的姓名、准考证号码填写清楚，将条形码准确粘贴在条形码区域内。2．答题时请按要求用笔。3．请按照题号顺序在答题卡各题目的答题区域内作答，超出答题区域书写的答案无效；在草稿纸、试卷上答题无效。4．作图可先使用铅笔画出，确定后必须用黑色字迹的签字笔描黑。5．保持卡面清洁，不要折暴、不要弄破、弄皱，不准使用涂改液、修正带、刮纸刀。 一、选择题(每小题3分,共30分)1．如图，正方形的对角线是菱形的一边，则等于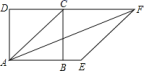（ ）A．135° B．45° C．22.5° D．30°2．在、、、、3中，最简二次根式的个数有（　　）A．4 B．3 C．2 D．13．多项式4x2﹣4与多项式x2﹣2x+1的公因式是（　　）A．x﹣1    B．x+1    C．x2﹣1    D．（x﹣1）24．不能判定四边形ABCD是平行四边形的题设是（　　）A．AB∥CD，AB＝CD B．AB＝CD，AD＝BCC．AD＝BC，∠A＝∠C D．AB∥CD，∠B＝∠D5．为了了解班级同学的家庭用水情况，小明在全班50名同学中，随机调查了10名同学家庭中一年的月平均用水量（单位：吨），绘制了条形统计图如图所示.这10名同学家庭中一年的月平均用水量的中位数是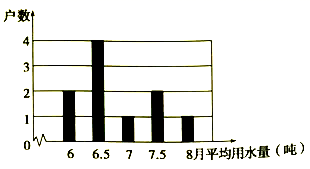（  ）A．6 B．6.5 C．7.5 D．86．用反证法证明命题“在三角形中，至多有一个内角是直角”时，应先假设（        ）A．至少有一个内角是直角 B．至少有两个内角是直角C．至多有一个内角是直角 D．至多有两个内角是直角7．如图，在一次实践活动课上，小明为了测量池塘B、C两点间的距离，他先在池塘的一侧选定一点A，然后测量出AB、AC的中点D、E，且DE=10m，于是可以计算出池塘B、C两点间的距离是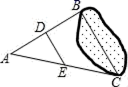（　　）            A．5m B．10m C．15m D．20m8．下面调查中，适合采用普查的是（  ）A．调查全国中学生心理健康现状 B．调查你所在的班级同学的身高情况C．调查我市食品合格情况 D．调查九江市电视台《九江新闻》收视率9．甲、乙两车从A城出发前往B城．在整个行程中，汽车离开A城的距离y与时刻t的对应关系如图所示，则下列结论错误的是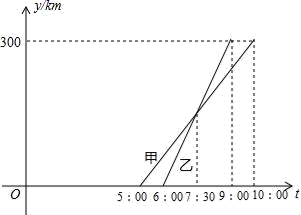（　　）A．A城和B城相距300kmB．甲先出发，乙先到达C．甲车的速度为60km/h，乙车的速度为100km/hD．6：00～7：30乙在甲前，7：30甲追上乙，7：30～9：00甲在乙前10．若分式有意义，则的取值范围是（  ）A． B． C． D．二、填空题(本大题共有6小题，每小题3分，共18分)11．计算：＝       ．12．如图，用9个全等的等边三角形，按图拼成一个几何图案，从该图案中可以找出_____个平行四边形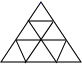．13．如图，O是矩形ABCD对角线AC的中点，M是AD的中点，若BC=8，OB=5，则OM的长为_____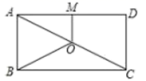14．利用因式分解计算：2012-1992=_________；15．如图，矩形中，，，在数轴上，若以点为圆心，对角线的长为半径作弧交数轴的正半轴于，则点的表示的数为_____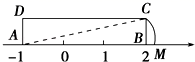．16．如图，在平行四边形ABCD中，AB＝2AD，BE平分∠ABC交CD于点E，作BF⊥AD，垂足为F，连接EF，小明得到三个结论：①∠FBC＝90°；②ED＝EB；③S△EBF＝S△EDF+S△EBC；则三个结论中一定成立的是_____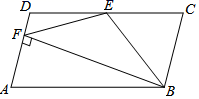．三、解下列各题(本大题共8小题，共72分)17．（8分）如图，在矩形纸片中，，.将矩形纸片折叠，使点与点重合，求折痕的长.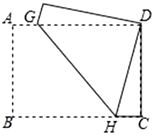   18．（8分）某学校打算招聘英语教师。对应聘者进行了听、说、读、写的英语水平测试，其中甲、乙两名应聘者的成绩（百分制）如下表所示。（1）如果学校想招聘说、读能力较强的英语教师，听、说、读、写成绩按照2：4：3：1的比确定，若在甲、乙两人中录取一人，请计算这两名应聘者的平均成绩（百分制）。从他们的成绩看，应该录取谁？（2）学校按照（1）中的成绩计算方法，将所有应聘者的最后成绩绘制成如图所示的频数分布直方图（每组分数段均包含左端数值，不包含右端数值，如最后左边一组分数为：）。①参加该校本次招聘英语教师的应聘者共有______________人（直接写出答案即可）。②学校决定由高分到低分录用3名教师，请判断甲、乙两人能否被录用？并说明理由。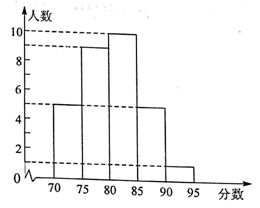   19．（8分）解不等式组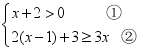：．   20．（8分）如图是某港口在某天从0时到12时的水位情况变化曲线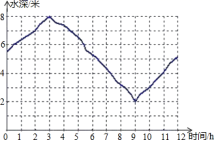．（1）在这一问题中，自变量是什么？（2）大约在什么时间水位最深，最深是多少？（3）大约在什么时间段水位是随着时间推移不断上涨的？   21．（8分）在平行四边形ABCD中，对角线AC、BD交于点O，点E、F在AC上，且AE=CF，求证：DE=BF. 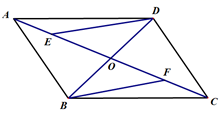  22．（10分）某校为了开展“书香墨香进校园”活动，购买了一批毛笔和墨水.已知毛笔的单位比墨水的单价多5元，购买毛笔用了450元，墨水用了150元，毛笔数量是墨水数量的2倍.求这批毛笔和墨水的数量分别是多少？   23．（10分）直线与x轴交于点A，与y轴交于点B，（1）求点A、B的坐标，画出直线AB；（2）点C在x轴上，且AC=AB，直接写出点C的坐标.   24．（12分）在四边形ABCD中，AB//CD，∠B=∠D．（1）求证：四边形ABCD为平行四边形；（2）若点P为对角线AC上的一点，PE⊥AB于E，PF⊥AD于F，且PE=PF,求证：四边形ABCD是菱形.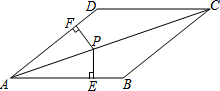   参考答案 一、选择题(每小题3分,共30分)1、C2、C3、A4、C5、B6、B7、D8、B9、D10、A 二、填空题(本大题共有6小题，每小题3分，共18分)11、312、113、3.14、80015、16、①③ 三、解下列各题(本大题共8小题，共72分)17、.18、（1）录取乙；（2）①30，②乙一定能被录用；甲不一定能被录用，见解析.19、2＜x≤120、（1）自变量是时间；（2）大约在3时水位最深，最深是8米；（3）在0到3时和9到12时，水位是随着时间推移不断上涨的．21、证明见解析.22、墨水的单价是10元，则毛笔的单价是15元．23、 (1)如图所示见解析；（2）C（1-，0）或C（1+，0）24、（1）证明见解析；（2）证明见解析.