2022-2023学年铜川市重点中学数学七年级第二学期期末达标测试试题含答案

2022-2023学年铜川市重点中学数学七年级第二学期期末达标测试试题

（时间：120分钟             分数：120分）

学校_______            年级_______        姓名_______

注意事项:

1．答题前，考生先将自己的姓名、准考证号码填写清楚，将条形码准确粘贴在条形码区域内。

2．答题时请按要求用笔。

3．请按照题号顺序在答题卡各题目的答题区域内作答，超出答题区域书写的答案无效；在草稿纸、试卷上答题无效。

4．作图可先使用铅笔画出，确定后必须用黑色字迹的签字笔描黑。

5．保持卡面清洁，不要折暴、不要弄破、弄皱，不准使用涂改液、修正带、刮纸刀。

一、选择题：本大题共12个小题，每小题3分，共36分.在每小题给出的四个选项中，只有一项是符合题目要求的.

1．如图，菱形ABCD中，AB=4，E，F分别是AB、BC的中点，P是AC上一动点，则PF+PE的最小值是（   ）

A．3 B． C．4 D．

2．某农科所对甲、乙两种小麦各选用10块面积相同的试验田进行种植试验，它们的平均亩产量分别是=610千克，=608千克，亩产量的方差分别是="29." 6，="2." 7. 则关于两种小麦推广种植的合理决策是 （ ）

A．甲的平均亩产量较高，应推广甲

B．甲、乙的平均亩产量相差不多，均可推广

C．甲的平均亩产量较高，且亩产量比较稳定，应推广甲

D．甲、乙的平均亩产量相差不多，但乙的亩产量比较稳定，应推广乙

3．边长是4且有一个内角为60°的菱形的面积为(   )

A．2 B．4 C．8 D．16

4．一辆汽车以50的速度行驶,行驶的路程与行驶的时间之间的关系式为,其中变量是（           ）

A．速度与路程 B．速度与时间 C．路程与时间 D．速度

5．某单位向一所希望小学赠送1080本课外书，现用A、B两种不同的包装箱进行包装，单独使用B型包装箱比单独使用A型包装箱可少用6个；已知每个B型包装箱比每个A型包装箱可多装15本课外书．若设每个A型包装箱可以装书x本，则根据题意列得方程为（　　）

A． B．

C． D．

6．函数自变量的值可以是（   ）

A．-1 B．0 C．1 D．2

7．下列调查适合普查的是（　　）

A．调查2011年3月份市场上西湖龙井茶的质量

B．了解萧山电视台188热线的收视率情况

C．网上调查萧山人民的生活幸福指数

D．了解全班同学身体健康状况

8．函数中自变量x的取值范围是（ ）

A．≥－3 B．≥－3且 C． D．且

9．将一元二次方程-6x-5=0化成=b的形式，则b等于（　　）

A．4 B．-4 C．14 D．-14

10．为考察甲、乙、丙三种小麦的长势，在同一时期分别从中随机抽取部分麦苗，计算后得到苗高（单位：cm）的方差为，，，则麦苗高度最整齐的是（　　）

A．甲 B．乙 C．丙 D．都一样

11．在平行四边形ABCD中，若∠A+∠C=260°，则∠D的度数为（   ）

A．120° B．100° C．50° D．130°

12．如图图形中，是中心对称图形，但不是轴对称图形的是（　　）

A． B．

C． D．

二、填空题（每题4分，满分20分，将答案填在答题纸上）

13．如图，在Rt△ABC中，D是斜边AB的中点，AB=2，则CD的长为_____.

14．一个n边形的内角和是720°，则n＝_____．

15．妈妈做了一份美味可口的菜品，为了了解菜品的咸淡是否适合，于是妈妈取了一点品尝，这应该属于___________（填普查或抽样调查）

16．若a，b都是实数，b＝+﹣2，则ab的值为_____．

17．如图，在平面直角坐标系中，函数y=2x和y=﹣x的图象分别为直线l1，l2，过点（1，0）作x轴的垂线交l2于点A1，过点A1作y轴的垂线交l2于点A2，过点A2作x轴的垂线交l2于点A3，过点A3作y轴的垂线交l2于点A4，…依次进行下去，则点A2017的坐标为_________________．

三、解答题 （本大题共7小题，共64分.解答应写出文字说明、证明过程或演算步骤.）

18．（5分）如图，在平面直角坐标系xOy中，已知直线AB：y＝x＋4交x轴于点A，交y轴于点B．直线CD：y＝－x－1与直线AB相交于点M，交x轴于点C，交y轴于点D．

(1)直接写出点B和点D的坐标．

(2)若点P是射线MD的一个动点，设点P的横坐标是x，△PBM的面积是S，求S与x之间的函数关系，并指出x的取值范围．

(3)当S＝10时，平面直角坐标系内是否存在点E，使以点B，E，P，M为顶点的四边形是平行四边形？若存在，共有几个这样的点？请求出其中一个点的坐标（写出求解过程）；若不存在，请说明理由．

19．（5分）已知直线 y＝kx＋b(k≠0)过点 F(0，1)，与抛物线 相交于B、C 两点

 (1)如图 1，当点 C 的横坐标为 1 时，求直线 BC 的解析式；

(2)在(1)的条件下，点 M 是直线 BC 上一动点，过点 M 作 y 轴的平行线，与抛物线交于点 D， 是否存在这样的点 M，使得以 M、D、O、F 为顶点的四边形为平行四边形？若存在，求出点 M 的坐标；若不存在，请说明理由；

(3)如图 2，设 B(m，n)(m＜0)，过点 E(0，－1)的直线 l∥x 轴，BR⊥l 于 R，CS⊥l 于 S，连接 FR、FS.试判断△ RFS 的形状，并说明理由．

20．（8分）如图，Rt△ABC中，∠ACB＝90°，D是边BC上一点，点E、F分别是线段AB、AD中点，联结CE、CF、EF．

（1）求证：△CEF≌△AEF；

（2）联结DE，当BD＝2CD时，求证：AD＝2DE．

21．（10分）如图，在四边形中，、、、分别是、、、的中点，.求证：.

22．（10分）如图,在平面直角坐标系中,Rt△ABC的三个顶点分别是A(-3,1),B(0,3),C(0,1).

(1)将△ABC以点C为旋转中心旋转180°,画出旋转后对应的△A1B1C;

(2)分别连接AB1,BA1后,求四边形AB1A1B的面积.

23．（12分）已知E、F分别是平行四边形ABCD的BC和DA边上的点，且CE=AF，问：DE与FB是否平行？说明理由．

参考答案

一、选择题：本大题共12个小题，每小题3分，共36分.在每小题给出的四个选项中，只有一项是符合题目要求的.

1、C

2、D

3、C

4、C

5、C

6、C

7、D

8、B

9、C

10、B

11、C

12、C

二、填空题（每题4分，满分20分，将答案填在答题纸上）

13、1

14、1

15、抽样调查

16、1

17、（21008，21009）．

三、解答题 （本大题共7小题，共64分.解答应写出文字说明、证明过程或演算步骤.）

18、（1）B（0，4），D（0，－1）；（2）（）；（3）存在，共有3个，E点为（4，）、（－6，－4）和

19、（1）；（2）存在；M点坐标为：（-3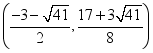，），，；（3）△RFS是直角三角形；证明见详解.

20、（1）见解析；（2）见解析.

21、见解析.

22、（1）画图见解析；（2）1

23、DE∥FB