


2022-2023学年重庆清化中学七年级数学第二学期期末达标检测试题含答案
展开
这是一份2022-2023学年重庆清化中学七年级数学第二学期期末达标检测试题含答案,共7页。试卷主要包含了答题时请按要求用笔,对于命题“已知,下列各等式成立的是等内容,欢迎下载使用。
2022-2023学年重庆清化中学七年级数学第二学期期末达标检测试题(时间:120分钟 分数:120分) 学校_______ 年级_______ 姓名_______ 注意事项:1.答题前,考生先将自己的姓名、准考证号码填写清楚,将条形码准确粘贴在条形码区域内。2.答题时请按要求用笔。3.请按照题号顺序在答题卡各题目的答题区域内作答,超出答题区域书写的答案无效;在草稿纸、试卷上答题无效。4.作图可先使用铅笔画出,确定后必须用黑色字迹的签字笔描黑。5.保持卡面清洁,不要折暴、不要弄破、弄皱,不准使用涂改液、修正带、刮纸刀。 一、选择题(每小题3分,共30分)1.下列不等式的变形中,不正确的是( )A.若![]() ,则
,则![]() B.若
B.若![]() ,则
,则![]() C.若
C.若![]() ,则
,则![]() D.若
D.若![]() ,则
,则![]() 2.如图,数轴上点A表示的数是-1,原点O是线段AB的中点,∠BAC=30,∠ABC=90°,以点A为圆心,AC长为半径画弧,交数轴于点D,则点D表示的数是
2.如图,数轴上点A表示的数是-1,原点O是线段AB的中点,∠BAC=30,∠ABC=90°,以点A为圆心,AC长为半径画弧,交数轴于点D,则点D表示的数是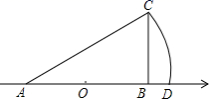 A.
A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 3.如图,已知点
3.如图,已知点![]() 在反比例函数
在反比例函数![]() (
(![]() )的图象上,作
)的图象上,作![]() ,边
,边![]() 在
在![]() 轴上,点
轴上,点![]() 为斜边
为斜边![]() 的中点,连结
的中点,连结![]() 并延长交
并延长交![]() 轴于点
轴于点![]() ,则
,则![]() 的面积为( )
的面积为( )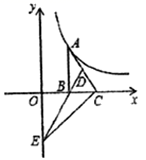 A.
A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 4.如果
4.如果![]() ,那么
,那么![]() 等于A.3:2 B.2:5 C.5:3 D.3:55.慢车和快车先后从甲地出发沿直线道路匀速驶向乙地,快车比慢车晚出发0.5小时,行驶一段时间后,快车途中休息,休息后继续按原速行驶,到达乙地后停止.慢车和快车离甲地的距离y(千米)与慢车行驶时间x(小时)之间的函数关系如图所示.有以下说法:①快车速度是120千米/小时;②慢车到达乙地比快车到达乙地晚了0.5小时;③点C坐标(
等于A.3:2 B.2:5 C.5:3 D.3:55.慢车和快车先后从甲地出发沿直线道路匀速驶向乙地,快车比慢车晚出发0.5小时,行驶一段时间后,快车途中休息,休息后继续按原速行驶,到达乙地后停止.慢车和快车离甲地的距离y(千米)与慢车行驶时间x(小时)之间的函数关系如图所示.有以下说法:①快车速度是120千米/小时;②慢车到达乙地比快车到达乙地晚了0.5小时;③点C坐标(![]() ,100);④线段BC对应的函数表达式为y=120x﹣60(0.5≤x≤
,100);④线段BC对应的函数表达式为y=120x﹣60(0.5≤x≤![]() );其中正确的个数有( )
);其中正确的个数有( )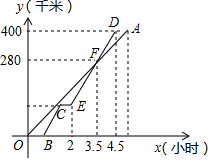 A.1 B.2 C.3 D.46.对于命题“已知:a∥b,b∥c,求证:a∥c”.如果用反证法,应先假设( )A.a不平行b B.b不平行c C.a⊥c D.a不平行c7.如图,将▱ABCD沿对角线AC进行折叠,折叠后点D落在点F处,AF交BC于点E,有下列结论:①△ABF≌△CFB;②AE=CE;③BF∥AC;④BE=CE,其中正确结论的个数是( )
A.1 B.2 C.3 D.46.对于命题“已知:a∥b,b∥c,求证:a∥c”.如果用反证法,应先假设( )A.a不平行b B.b不平行c C.a⊥c D.a不平行c7.如图,将▱ABCD沿对角线AC进行折叠,折叠后点D落在点F处,AF交BC于点E,有下列结论:①△ABF≌△CFB;②AE=CE;③BF∥AC;④BE=CE,其中正确结论的个数是( )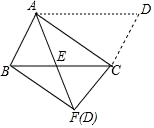 A.1 B.2 C.3 D.48.已知x1,x2是方程
A.1 B.2 C.3 D.48.已知x1,x2是方程![]() 的两个根,则
的两个根,则![]() 的值为( )A.1 B.-1 C.2 D.-29.下列各等式成立的是( )A.
的值为( )A.1 B.-1 C.2 D.-29.下列各等式成立的是( )A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 10.如图,点O是AC的中点,将面积为4cm2的菱形ABCD沿对角线AC方向平移AO长度得到菱形OB′C′D′,则图中阴影部分的面积是( )
10.如图,点O是AC的中点,将面积为4cm2的菱形ABCD沿对角线AC方向平移AO长度得到菱形OB′C′D′,则图中阴影部分的面积是( )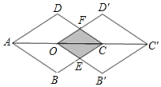 A.1cm2 B.2cm2 C.3cm2 D.4cm2二、填空题(本大题共有6小题,每小题3分,共18分)11.在●〇●〇〇●〇〇〇●〇〇〇〇●〇〇〇〇〇中,空心圈“〇”出现的频率是_____.12.如图,以△ABC的三边为边分别作等边△ACD、△ABE、△BCF, 则下列结论:①△EBF≌△DFC;②四边形AEFD为平行四边形;③当AB=AC,∠BAC=1200时,四边形AEFD是正方形.其中正确的结论是 .(请写出正确结论的番号).
A.1cm2 B.2cm2 C.3cm2 D.4cm2二、填空题(本大题共有6小题,每小题3分,共18分)11.在●〇●〇〇●〇〇〇●〇〇〇〇●〇〇〇〇〇中,空心圈“〇”出现的频率是_____.12.如图,以△ABC的三边为边分别作等边△ACD、△ABE、△BCF, 则下列结论:①△EBF≌△DFC;②四边形AEFD为平行四边形;③当AB=AC,∠BAC=1200时,四边形AEFD是正方形.其中正确的结论是 .(请写出正确结论的番号).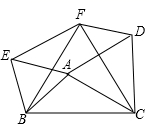 13.如图,菱形ABCD中,AC、BD交于点O,DE⊥BC于点E,连接OE,若∠ABC=120°,则∠OED=______.
13.如图,菱形ABCD中,AC、BD交于点O,DE⊥BC于点E,连接OE,若∠ABC=120°,则∠OED=______.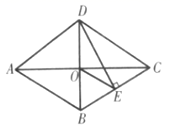 14.若一个正多边形的每一个外角都是
14.若一个正多边形的每一个外角都是![]() ,则这个正多边形的边数为__________.15.计算(4
,则这个正多边形的边数为__________.15.计算(4![]() +
+![]() )÷3
)÷3![]() 的结果是_____.16.在菱形
的结果是_____.16.在菱形![]() 中,
中,![]() ,其周长为
,其周长为![]() ,则菱形的面积为__
,则菱形的面积为__![]() .三、解下列各题(本大题共8小题,共72分)17.(8分)在菱形ABCD中,∠ABC=60°,P是射线BD上一动点,以AP为边向右侧作等边△APE,连接CE.(1)如图1,当点P在菱形ABCD内部时,则BP与CE的数量关系是 ,CE与AD的位置关系是 .(2)如图2,当点P在菱形ABCD外部时,(1)中的结论是否还成立?若成立,请予以证明;若不成立,请说明理由;(3)如图2,连接BE,若AB=2
.三、解下列各题(本大题共8小题,共72分)17.(8分)在菱形ABCD中,∠ABC=60°,P是射线BD上一动点,以AP为边向右侧作等边△APE,连接CE.(1)如图1,当点P在菱形ABCD内部时,则BP与CE的数量关系是 ,CE与AD的位置关系是 .(2)如图2,当点P在菱形ABCD外部时,(1)中的结论是否还成立?若成立,请予以证明;若不成立,请说明理由;(3)如图2,连接BE,若AB=2![]() ,BE=2
,BE=2![]() ,求AP的长.
,求AP的长.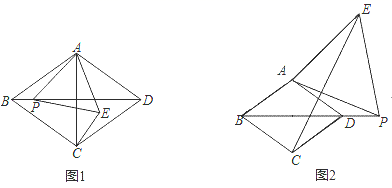 18.(8分)(1)如图1,在正方形ABCD中,M是BC边(不含端点B、C)上任意一点,P是BC延长线上一点,N是∠DCP的平分线上一点.若∠AMN=90°,求证:AM=MN.下面给出一种证明的思路,你可以按这一思路证明,也可以选择另外的方法证明.证明:在边AB上截取AE=MC,连ME.正方形ABCD中,∠B=∠BCD=90°,AB=BC.∴∠NMC=180°—∠AMN—∠AMB=180°—∠B—∠AMB=∠MAB=∠MAE.(下面请你完成余下的证明过程)
18.(8分)(1)如图1,在正方形ABCD中,M是BC边(不含端点B、C)上任意一点,P是BC延长线上一点,N是∠DCP的平分线上一点.若∠AMN=90°,求证:AM=MN.下面给出一种证明的思路,你可以按这一思路证明,也可以选择另外的方法证明.证明:在边AB上截取AE=MC,连ME.正方形ABCD中,∠B=∠BCD=90°,AB=BC.∴∠NMC=180°—∠AMN—∠AMB=180°—∠B—∠AMB=∠MAB=∠MAE.(下面请你完成余下的证明过程)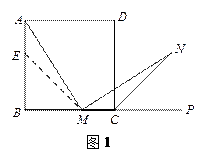
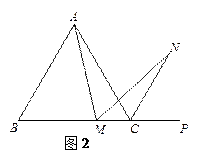 (2)若将(1)中的“正方形ABCD”改为“正三角形ABC”(如图2),N是∠ACP的平分线上一点,则当∠AMN=60°时,结论AM=MN是否还成立?请说明理由.(3)若将(1)中的“正方形ABCD”改为“正
(2)若将(1)中的“正方形ABCD”改为“正三角形ABC”(如图2),N是∠ACP的平分线上一点,则当∠AMN=60°时,结论AM=MN是否还成立?请说明理由.(3)若将(1)中的“正方形ABCD”改为“正![]() 边形ABCD……X”,请你作出猜想:当∠AMN=" " °时,结论AM=MN仍然成立.(直接写出答案,不需要证明) 19.(8分)学校需要采购一批演出服装,A、B两家制衣公司都愿成为这批服装的供应商.经了解:两家公司生产的这款演出服装的质量和单价都相同,即男装每套120元,女装每套100元.经洽谈协商:A公司给出的优惠条件是,全部服装按单价打七折,但校方需承担2200元的运费;B公司的优惠条件是男女装均按每套100元打八折,公司承担运费.另外根据大会组委会要求,参加演出的女生人数应是男生人数的2倍少100人,如果设参加演出的男生有x人.(1)分别写出学校购买A、B两公司服装所付的总费用y1(元)和y2(元)与参演男生人数x之间的函数关系式;(2)问:该学校购买哪家制衣公司的服装比较合算?请说明理由. 20.(8分)阅读理解题:定义:如果一个数的平方等于-1,记为i2=-1,这个数i叫做虚数单位,把形如a+bi(a,b为实数)的数叫做复数,其中a叫这个复数的实部,b叫做这个复数的虚部,它的加、减,乘法运算与整式的加、减、乘法运算类似.例如计算:(2-i)+(5+3i)=(2+5)+(-1+3)i=7+2i; (1+i)×(2-i)=1×2-i+2×i-i2=2+(-1+2)i+1=3+i;根据以上信息,完成下列问题:(1)填空:i3= ,i4= ;(2)计算:(1+i)×(3-4i);(3)计算:i+i2+i3+…+i1. 21.(8分)已知:如图,在△ABC中,AB=AC=4cm,将△ABC沿CA方向平移4cm得到△EFA,连接BE,BF;BE与AF交于点G(1)判断BE与AF的位置关系,并说明理由;(2)若∠BEC=15°,求四边形BCEF的面积.
边形ABCD……X”,请你作出猜想:当∠AMN=" " °时,结论AM=MN仍然成立.(直接写出答案,不需要证明) 19.(8分)学校需要采购一批演出服装,A、B两家制衣公司都愿成为这批服装的供应商.经了解:两家公司生产的这款演出服装的质量和单价都相同,即男装每套120元,女装每套100元.经洽谈协商:A公司给出的优惠条件是,全部服装按单价打七折,但校方需承担2200元的运费;B公司的优惠条件是男女装均按每套100元打八折,公司承担运费.另外根据大会组委会要求,参加演出的女生人数应是男生人数的2倍少100人,如果设参加演出的男生有x人.(1)分别写出学校购买A、B两公司服装所付的总费用y1(元)和y2(元)与参演男生人数x之间的函数关系式;(2)问:该学校购买哪家制衣公司的服装比较合算?请说明理由. 20.(8分)阅读理解题:定义:如果一个数的平方等于-1,记为i2=-1,这个数i叫做虚数单位,把形如a+bi(a,b为实数)的数叫做复数,其中a叫这个复数的实部,b叫做这个复数的虚部,它的加、减,乘法运算与整式的加、减、乘法运算类似.例如计算:(2-i)+(5+3i)=(2+5)+(-1+3)i=7+2i; (1+i)×(2-i)=1×2-i+2×i-i2=2+(-1+2)i+1=3+i;根据以上信息,完成下列问题:(1)填空:i3= ,i4= ;(2)计算:(1+i)×(3-4i);(3)计算:i+i2+i3+…+i1. 21.(8分)已知:如图,在△ABC中,AB=AC=4cm,将△ABC沿CA方向平移4cm得到△EFA,连接BE,BF;BE与AF交于点G(1)判断BE与AF的位置关系,并说明理由;(2)若∠BEC=15°,求四边形BCEF的面积.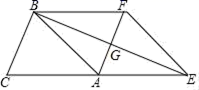 22.(10分)如图,某同学想测量旗杆的高度,他在某一时刻测得1米长的竹竿竖直放置时影长为1.5米,在同一时刻测量旗杆的影长时,因旗杆靠近一楼房,影子不全落在地面上,有一部分落在墙上,他测得落在地面上的影长为21米,落在墙上的影高为6米,求旗杆的高度.
22.(10分)如图,某同学想测量旗杆的高度,他在某一时刻测得1米长的竹竿竖直放置时影长为1.5米,在同一时刻测量旗杆的影长时,因旗杆靠近一楼房,影子不全落在地面上,有一部分落在墙上,他测得落在地面上的影长为21米,落在墙上的影高为6米,求旗杆的高度. 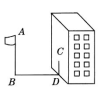 23.(10分)小倩和爸爸、妈妈到人民公园游玩,回到家后,她利用平面直角坐标系画出了公园的景区地图,如图所示.可是她忘记了在图中标出原点和x轴、y轴;只知道游乐园D的坐标为(2,﹣2).(1)画出平面直角坐标系;(2)求出其他各景点的坐标.
23.(10分)小倩和爸爸、妈妈到人民公园游玩,回到家后,她利用平面直角坐标系画出了公园的景区地图,如图所示.可是她忘记了在图中标出原点和x轴、y轴;只知道游乐园D的坐标为(2,﹣2).(1)画出平面直角坐标系;(2)求出其他各景点的坐标.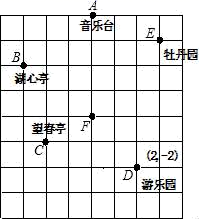 24.(12分)如图,在平行四边形ABCD中,E,F为对角线BD上的两点,且∠DAE=∠BCF.求证:(1)AE=CF;(2)四边形AECF是平行四边形.
24.(12分)如图,在平行四边形ABCD中,E,F为对角线BD上的两点,且∠DAE=∠BCF.求证:(1)AE=CF;(2)四边形AECF是平行四边形.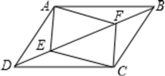 参考答案 一、选择题(每小题3分,共30分)1、D2、D3、A4、B5、D6、D7、C8、B9、C10、A 二、填空题(本大题共有6小题,每小题3分,共18分)11、0.112、①②.13、30°14、115、216、
参考答案 一、选择题(每小题3分,共30分)1、D2、D3、A4、B5、D6、D7、C8、B9、C10、A 二、填空题(本大题共有6小题,每小题3分,共18分)11、0.112、①②.13、30°14、115、216、![]() 三、解下列各题(本大题共8小题,共72分)17、(1)BP=CE,CE⊥AD;(2)结论仍然成立,理由见解析;(3)2
三、解下列各题(本大题共8小题,共72分)17、(1)BP=CE,CE⊥AD;(2)结论仍然成立,理由见解析;(3)2![]() 18、(1)见详解;(2)见详解;(3)
18、(1)见详解;(2)见详解;(3)![]() 19、(1)y1=224x-4 800;y2=240x-8 000;(2)当男生人数少于200时,购买B公司服装合算;当男生人数等于200时,购买A,B公司服装都一样;当男生人数大于200时,购买A公司服装合算,理由见解析20、(2)-i,2;(2)7-i;(3)i-2.21、(1)BE⊥AF,理由详见解析;(2)1.22、20米.23、A(0,4),B(﹣3,2),C(﹣2,﹣1),E(3,3),F(0,0).24、(1)详见解析;(2)详见解析
19、(1)y1=224x-4 800;y2=240x-8 000;(2)当男生人数少于200时,购买B公司服装合算;当男生人数等于200时,购买A,B公司服装都一样;当男生人数大于200时,购买A公司服装合算,理由见解析20、(2)-i,2;(2)7-i;(3)i-2.21、(1)BE⊥AF,理由详见解析;(2)1.22、20米.23、A(0,4),B(﹣3,2),C(﹣2,﹣1),E(3,3),F(0,0).24、(1)详见解析;(2)详见解析
相关试卷
这是一份2023-2024学年重庆清化中学八年级数学第一学期期末检测试题含答案,共8页。试卷主要包含了考生必须保证答题卡的整洁,若分式的值为0,则x的取值是等内容,欢迎下载使用。
这是一份重庆市南开中学2022-2023学年数学七年级第二学期期末达标测试试题含答案,共7页。试卷主要包含了考生要认真填写考场号和座位序号,五边形的内角和是等内容,欢迎下载使用。
这是一份重庆市两江巴蜀中学2022-2023学年数学七年级第二学期期末达标检测试题含答案,共7页。试卷主要包含了考生要认真填写考场号和座位序号,若是一个完全平方式,则k的值是等内容,欢迎下载使用。









