


东北师大附中净月实验学校2022-2023学年七年级数学第二学期期末综合测试模拟试题含答案
展开
这是一份东北师大附中净月实验学校2022-2023学年七年级数学第二学期期末综合测试模拟试题含答案,共8页。试卷主要包含了已知一组数据,如图,直线l1等内容,欢迎下载使用。
东北师大附中净月实验学校2022-2023学年七年级数学第二学期期末综合测试模拟试题(时间:120分钟 分数:120分) 学校_______ 年级_______ 姓名_______ 注意事项:1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其它答案标号。回答非选择题时,将答案写在答题卡上,写在本试卷上无效。3.考试结束后,将本试卷和答题卡一并交回。 一、选择题(每小题3分,共30分)1.在直角三角形中,自锐角顶点所引的两条中线长为![]() 和
和![]() ,那么这个直角三角形的斜边长为( )A.6 B.7 C.2 D.2
,那么这个直角三角形的斜边长为( )A.6 B.7 C.2 D.2![]() 2.已知,四边形ABCD的对角线AC⊥BD,E,F,G,H分别是边AB,BC,CD,DA的中点,那么四边形EFGH是( )A.平行四边形 B.矩形 C.菱形 D.正方形3.下列命题正确的是( )A.对角线互相垂直的四边形是菱形B.一组对边相等,另一组对边平行的四边形是平行四边形C.对角线相等的四边形是矩形D.对角线互相垂直平分且相等的四边形是正方形4.已知一组数据:10,8,6,10,8,13,11,12,10,10,7,9,8,12,9,11,12,9,10,11,则分组后频率为0.2的一组是( )A.6~7 B.8~9 C.10~11 D.12~135.如图,直线l1:y=x+1与直线l2:y=mx+n相交于点P(a,2),则关于不等式x+1≥mx+n的解集是( )
2.已知,四边形ABCD的对角线AC⊥BD,E,F,G,H分别是边AB,BC,CD,DA的中点,那么四边形EFGH是( )A.平行四边形 B.矩形 C.菱形 D.正方形3.下列命题正确的是( )A.对角线互相垂直的四边形是菱形B.一组对边相等,另一组对边平行的四边形是平行四边形C.对角线相等的四边形是矩形D.对角线互相垂直平分且相等的四边形是正方形4.已知一组数据:10,8,6,10,8,13,11,12,10,10,7,9,8,12,9,11,12,9,10,11,则分组后频率为0.2的一组是( )A.6~7 B.8~9 C.10~11 D.12~135.如图,直线l1:y=x+1与直线l2:y=mx+n相交于点P(a,2),则关于不等式x+1≥mx+n的解集是( )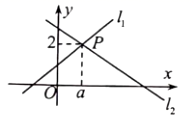 A.x≥m B.x≥2 C.x≥1 D.x≥﹣16.如图,在平行四边形ABCD中,∠B=70°,AE平分∠BAD交BC于点E,CF∥AE交AE于点F,则∠1=( )
A.x≥m B.x≥2 C.x≥1 D.x≥﹣16.如图,在平行四边形ABCD中,∠B=70°,AE平分∠BAD交BC于点E,CF∥AE交AE于点F,则∠1=( )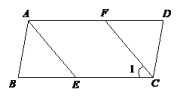 A.45° B.55° C.50° D.60°7.一种微粒的半径是4×10-5米,用小数表示为( )A.0.000004米 B.0.000004米 C.0.00004米 D.0.0004米8.某企业1~5月份利润的变化情况如图所示,以下说法与图中反映的信息相符的是( ).
A.45° B.55° C.50° D.60°7.一种微粒的半径是4×10-5米,用小数表示为( )A.0.000004米 B.0.000004米 C.0.00004米 D.0.0004米8.某企业1~5月份利润的变化情况如图所示,以下说法与图中反映的信息相符的是( ).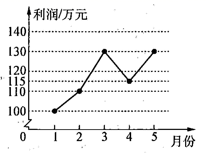 A.1~2月份利润的增长快于2~3月份利润的增长B.1~4月份利润的极差与1~5月份利润的极差不同C.1~5月份利润的众数是130万元D.1~5月份利润的中位数为120万元9.如图,在平行四边形ABCD中,∠BAC=78°,∠ACB=38°,则∠D的度数是( )
A.1~2月份利润的增长快于2~3月份利润的增长B.1~4月份利润的极差与1~5月份利润的极差不同C.1~5月份利润的众数是130万元D.1~5月份利润的中位数为120万元9.如图,在平行四边形ABCD中,∠BAC=78°,∠ACB=38°,则∠D的度数是( ) 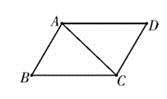 A.52° B.64° C.78° D.38°10. “龟兔赛跑”这则寓言故事讲述的是比赛中兔子开始领先,但它因为骄傲在途中睡觉,而乌龟一直坚持爬行最终贏得比赛,下列函数图象可以体现这一故事过程的是( )A.
A.52° B.64° C.78° D.38°10. “龟兔赛跑”这则寓言故事讲述的是比赛中兔子开始领先,但它因为骄傲在途中睡觉,而乌龟一直坚持爬行最终贏得比赛,下列函数图象可以体现这一故事过程的是( )A.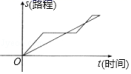 B.
B.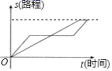 C.
C.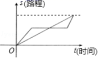 D.
D.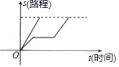 二、填空题(本大题共有6小题,每小题3分,共18分)11.如图,“今有直角三角形,勾(短直角边)长为5,股(长直角边)长为12,河该直角三角形能容纳的如图所示的正方形
二、填空题(本大题共有6小题,每小题3分,共18分)11.如图,“今有直角三角形,勾(短直角边)长为5,股(长直角边)长为12,河该直角三角形能容纳的如图所示的正方形![]() 边长是多少?”,该问题的答案是______.
边长是多少?”,该问题的答案是______.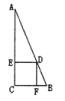 12.已知一次函数y=mx+n与x轴的交点为(﹣3,0),则方程mx+n=0的解是_____.13.正方形
12.已知一次函数y=mx+n与x轴的交点为(﹣3,0),则方程mx+n=0的解是_____.13.正方形![]() ,
,![]() ,
,![]() 按如图所示放置,点
按如图所示放置,点![]() 、
、![]() 、
、![]() 在直线
在直线![]() 上,点
上,点![]() 、
、![]() 、
、![]() 在x轴上,则
在x轴上,则![]() 的坐标是________.
的坐标是________.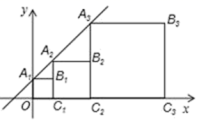 14.小强调查“每人每天的用水量”这一问题时,收集到80个数据,最大数据是70升,最小数据是42升,若取组距为4,则应分为_________组绘制频数分布表.15.如图,在△ABC中,∠CAB=70º,在同一平面内,将△ABC绕点
14.小强调查“每人每天的用水量”这一问题时,收集到80个数据,最大数据是70升,最小数据是42升,若取组距为4,则应分为_________组绘制频数分布表.15.如图,在△ABC中,∠CAB=70º,在同一平面内,将△ABC绕点![]() 逆时针旋转50º到△
逆时针旋转50º到△![]() 的位置,则∠
的位置,则∠![]() = _________度.
= _________度.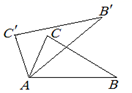 16.二次根式
16.二次根式![]() 有意义的条件是__________.三、解下列各题(本大题共8小题,共72分)17.(8分)某中学对全校1200名学生进行“校园安全知识”的教育活动,从1200名学生中随机抽取部分学生进行测试,成绩评定按从高分到低分排列分为
有意义的条件是__________.三、解下列各题(本大题共8小题,共72分)17.(8分)某中学对全校1200名学生进行“校园安全知识”的教育活动,从1200名学生中随机抽取部分学生进行测试,成绩评定按从高分到低分排列分为![]() 四个等级,绘制了图①、图②两幅不完整的统计图,请结合图中所给信息解答下列问题:
四个等级,绘制了图①、图②两幅不完整的统计图,请结合图中所给信息解答下列问题: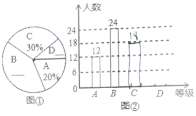 (1)求本次抽查的学生共有______人;(2)将条形统计图和扇形统计图补充完整;(3)扇形统计图中“
(1)求本次抽查的学生共有______人;(2)将条形统计图和扇形统计图补充完整;(3)扇形统计图中“![]() ”所在扇形圆心角的度数为______;(4)估计全校“
”所在扇形圆心角的度数为______;(4)估计全校“![]() ”等级的学生有______人 18.(8分)有一工程需在规定日期x天内完成,如果甲单独工作刚好能够按期完成:如果乙单独工作就要超过规定日期3天.(1)甲的工作效率为 ,乙的工作效率为 .(用含x的代数式表示)(2)若甲、乙合作2天后余下的工程由乙单独完成刚好在规定日期完成,求x的值. 19.(8分)在正方形ABCD中,E是边CD上一点(点E不与点C、D重合),连结BE.
”等级的学生有______人 18.(8分)有一工程需在规定日期x天内完成,如果甲单独工作刚好能够按期完成:如果乙单独工作就要超过规定日期3天.(1)甲的工作效率为 ,乙的工作效率为 .(用含x的代数式表示)(2)若甲、乙合作2天后余下的工程由乙单独完成刚好在规定日期完成,求x的值. 19.(8分)在正方形ABCD中,E是边CD上一点(点E不与点C、D重合),连结BE.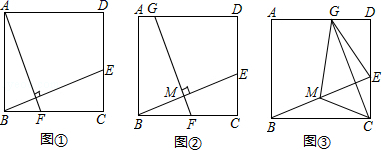 (感知)如图①,过点A作AF⊥BE交BC于点F.易证△ABF≌△BCE.(不需要证明)(探究)如图②,取BE的中点M,过点M作FG⊥BE交BC于点F,交AD于点G.(1)求证:BE=FG.(2)连结CM,若CM=1,则FG的长为 .(应用)如图③,取BE的中点M,连结CM.过点C作CG⊥BE交AD于点G,连结EG、MG.若CM=3,则四边形GMCE的面积为 . 20.(8分)某年5月,我国南方某省A、B两市遭受严重洪涝灾害,1.5万人被迫转移,邻近县市C、D获知A、B两市分别急需救灾物资200吨和300吨的消息后,决定调运物资支援灾区. 已知C市有救灾物资240吨,D市有救灾物资260吨,现将这些救灾物资全部调往A、B两市. 已知从C市运往A、B两市的费用分别为每吨20元和25元,从D市运往往A、B两市的费用分别为每吨15元和30元,设从C市运往B市的救灾物资为x吨.(1)请填写下表;
(感知)如图①,过点A作AF⊥BE交BC于点F.易证△ABF≌△BCE.(不需要证明)(探究)如图②,取BE的中点M,过点M作FG⊥BE交BC于点F,交AD于点G.(1)求证:BE=FG.(2)连结CM,若CM=1,则FG的长为 .(应用)如图③,取BE的中点M,连结CM.过点C作CG⊥BE交AD于点G,连结EG、MG.若CM=3,则四边形GMCE的面积为 . 20.(8分)某年5月,我国南方某省A、B两市遭受严重洪涝灾害,1.5万人被迫转移,邻近县市C、D获知A、B两市分别急需救灾物资200吨和300吨的消息后,决定调运物资支援灾区. 已知C市有救灾物资240吨,D市有救灾物资260吨,现将这些救灾物资全部调往A、B两市. 已知从C市运往A、B两市的费用分别为每吨20元和25元,从D市运往往A、B两市的费用分别为每吨15元和30元,设从C市运往B市的救灾物资为x吨.(1)请填写下表;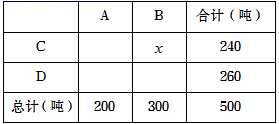 (2)设C、D两市的总运费为W元,求W与x之间的函数关系式,并写出自变量x的取值范围;(3)经过抢修,从C市到B市的路况得到了改善,缩短了运输时间,运费每吨减少n元(n>0),其余路线运费不变,若C、D两市的总运费的最小值不小于10080元,求n的取值范围. 21.(8分)为了推动我区教育教学发展,加快教师的成长与提升,学年度某名师工作室开展了多次送教下乡活动.在某次研讨课活动中,为了分析某节复习课的教学效果,课前,张老师让八(
(2)设C、D两市的总运费为W元,求W与x之间的函数关系式,并写出自变量x的取值范围;(3)经过抢修,从C市到B市的路况得到了改善,缩短了运输时间,运费每吨减少n元(n>0),其余路线运费不变,若C、D两市的总运费的最小值不小于10080元,求n的取值范围. 21.(8分)为了推动我区教育教学发展,加快教师的成长与提升,学年度某名师工作室开展了多次送教下乡活动.在某次研讨课活动中,为了分析某节复习课的教学效果,课前,张老师让八(![]() )班每位同学做
)班每位同学做![]() 道类似题目(与这节课内容相关)析某节复至少容对,解题情况如图所示:课后,再让学生做
道类似题目(与这节课内容相关)析某节复至少容对,解题情况如图所示:课后,再让学生做![]() 道类似的题目.结果如表所示.已知每位学生至少答对题.
道类似的题目.结果如表所示.已知每位学生至少答对题.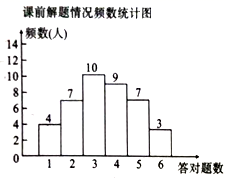
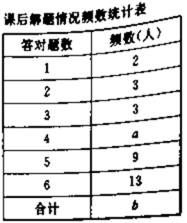 (1)根据图表信息填空:
(1)根据图表信息填空:![]() ;
;![]() .(2)该班课前解题时答对题数的众数是 ;课后答对题数的中位数是 .(3)通过计算课前,课后学生答对题数的平均数,评价这节复习课的教学效果. 22.(10分)矩形ABCO中,O(0,0),C(0,3),A(a,0),(a≥3),以A为旋转中心顺时针旋转矩形ABCO得到矩形AFED.
.(2)该班课前解题时答对题数的众数是 ;课后答对题数的中位数是 .(3)通过计算课前,课后学生答对题数的平均数,评价这节复习课的教学效果. 22.(10分)矩形ABCO中,O(0,0),C(0,3),A(a,0),(a≥3),以A为旋转中心顺时针旋转矩形ABCO得到矩形AFED.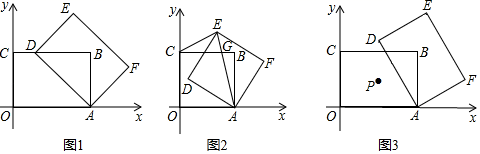 (1)如图1,当点D落在边BC上时,求BD的长(用a的式子表示);(2)如图2,当a=3时,矩形AFED的对角线AE交矩形ABCO的边BC于点G,连结CE,若△CGE是等腰三角形,求直线BE的解析式;(3)如图3,矩形ABCO的对称中心为点P,当P,B关于AD对称时,求出a的值,此时在x轴、y轴上是否分别存在M,N使得四边形EFMN为平行四边形,若存在直接写出M,N坐标,不存在说明理由. 23.(10分)某物流公司引进A,B两种机器人用来搬运某种货物,这两种机器人充满电后可以连续搬运5小时,A种机器人于某日0时开始搬运,过了1小时,B种机器人也开始搬运,如图,线段OG表示A种机器人的搬运量yA(千克)与时间x(时)的函数图象,根据图象提供的信息,解答下列问题:
(1)如图1,当点D落在边BC上时,求BD的长(用a的式子表示);(2)如图2,当a=3时,矩形AFED的对角线AE交矩形ABCO的边BC于点G,连结CE,若△CGE是等腰三角形,求直线BE的解析式;(3)如图3,矩形ABCO的对称中心为点P,当P,B关于AD对称时,求出a的值,此时在x轴、y轴上是否分别存在M,N使得四边形EFMN为平行四边形,若存在直接写出M,N坐标,不存在说明理由. 23.(10分)某物流公司引进A,B两种机器人用来搬运某种货物,这两种机器人充满电后可以连续搬运5小时,A种机器人于某日0时开始搬运,过了1小时,B种机器人也开始搬运,如图,线段OG表示A种机器人的搬运量yA(千克)与时间x(时)的函数图象,根据图象提供的信息,解答下列问题: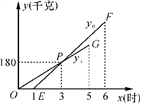 (1)求yB关于x的函数解析式;(2)如果A,B两种机器人连续搬运5小时,那么B种机器人比A种机器人多搬运了多少千克? 24.(12分)如图,
(1)求yB关于x的函数解析式;(2)如果A,B两种机器人连续搬运5小时,那么B种机器人比A种机器人多搬运了多少千克? 24.(12分)如图,![]() ,
,![]() 分别表示使用一种白炽灯和一种节能灯的费用
分别表示使用一种白炽灯和一种节能灯的费用![]() (费用
(费用![]() 灯的售价
灯的售价![]() 电费,单位:元)与照明时间
电费,单位:元)与照明时间![]() (小时)的函数图象,假设两种灯的使用寿命都是
(小时)的函数图象,假设两种灯的使用寿命都是![]() 小时,照明效果一样.
小时,照明效果一样.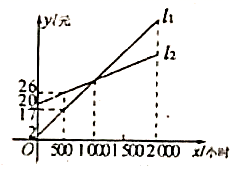 (1)根据图象分别求出
(1)根据图象分别求出![]() ,
,![]() 的函数表达式;(2)小亮认为节能灯一定比白炽灯省钱,你是如何想的? 参考答案 一、选择题(每小题3分,共30分)1、A2、B3、D4、D5、C6、B7、C8、C9、B10、B 二、填空题(本大题共有6小题,每小题3分,共18分)11、
的函数表达式;(2)小亮认为节能灯一定比白炽灯省钱,你是如何想的? 参考答案 一、选择题(每小题3分,共30分)1、A2、B3、D4、D5、C6、B7、C8、C9、B10、B 二、填空题(本大题共有6小题,每小题3分,共18分)11、![]() 12、x=﹣1.13、
12、x=﹣1.13、![]() 14、115、1016、
14、115、1016、![]() 三、解下列各题(本大题共8小题,共72分)17、(1)60;(2)见解析;(3)
三、解下列各题(本大题共8小题,共72分)17、(1)60;(2)见解析;(3)![]() ;(4)1.18、(1)
;(4)1.18、(1)![]() ,
,![]() ;(2)规定的时间是6天.19、(1)证明见解析;(1)1,2.20、(1)如表见解析;(2)W=-10x+11200,
;(2)规定的时间是6天.19、(1)证明见解析;(1)1,2.20、(1)如表见解析;(2)W=-10x+11200,![]() ; (1)
; (1)![]() 21、(1)
21、(1)![]() ;
;![]() ;(2)
;(2)![]() 题,
题,![]() 题;(3)这节复习课的教学效果明显.,22、(1)BD=
题;(3)这节复习课的教学效果明显.,22、(1)BD=![]() ;(2)y=﹣x+6;(3)M(
;(2)y=﹣x+6;(3)M(![]() ,0),N(0,
,0),N(0,![]() )23、 (1) yB=1x-1(1≤x≤6).(2)如果A,B两种机器人各连续搬运5小时,B种机器人比A种机器人多搬运了150千克.24、(1)
)23、 (1) yB=1x-1(1≤x≤6).(2)如果A,B两种机器人各连续搬运5小时,B种机器人比A种机器人多搬运了150千克.24、(1)![]() 的函数表达式为
的函数表达式为![]() ,
,![]() 的函数表达式为
的函数表达式为![]()
![]() ;(2)小亮的想法是错误的,若两灯同时点亮,当
;(2)小亮的想法是错误的,若两灯同时点亮,当![]() 时,白炽灯省钱;当
时,白炽灯省钱;当![]() 时,两种灯费用相同;当
时,两种灯费用相同;当![]() 时,节能灯省钱.
时,节能灯省钱.
相关试卷
这是一份东北师大附中净月实验学校2024-2025学年九上数学开学调研模拟试题【含答案】,共25页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
这是一份2024-2025学年东北师大附中净月实验学校九年级数学第一学期开学检测试题【含答案】,共22页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
这是一份东北师大附中净月实验学校2023-2024学年数学九上期末质量跟踪监视试题含答案,共8页。试卷主要包含了方程的解的个数为等内容,欢迎下载使用。









