九江市重点中学2022-2023学年数学七年级第二学期期末质量跟踪监视模拟试题含答案

九江市重点中学2022-2023学年数学七年级第二学期期末质量跟踪监视模拟试题

（时间：120分钟             分数：120分）

学校_______            年级_______        姓名_______

考生请注意：

1．答题前请将考场、试室号、座位号、考生号、姓名写在试卷密封线内，不得在试卷上作任何标记。

2．第一部分选择题每小题选出答案后，需将答案写在试卷指定的括号内，第二部分非选择题答案写在试卷题目指定的位置上。

3．考生必须保证答题卡的整洁。考试结束后，请将本试卷和答题卡一并交回。

一、选择题(每小题3分,共30分)

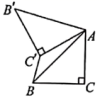
1．如图，已知中，，，将绕点顺时针方向旋转到的位置，连接，则的长为(   )

A． B． C． D．

2．下列二次根式能与合并为一项的是（   ）

A． B． C． D．

3．甲、乙、丙、丁四名射击队员考核赛的平均成绩（环）及方差统计如表，现要根据这些数据，从中选出一人参加比赛，如果你是教练员，你的选择是（　　）

A．甲 B．乙 C．丙 D．丁

4．剪纸艺术是中国传统的民间工艺．下列剪纸的图案中，属于中心对称图形的是（    ）

A． B． C． D．

5．使式子有意义的x的值是（　　）

A．x≥1 B．x≤1 C．x≥﹣1 D．x≤2

6．如图,点P是双曲线y= (x>0)上的一个动点,过点P作PA⊥x轴于点A,当点P从左向右移动时,△OPA的面积(    )

A．逐渐变大 B．逐渐变小 C．先增大后减小 D．保持不变

7．如果一组数据1、2、x、5、6的众数是6，则这组数据的中位数是（   ）

A．1 B．2 C．5 D．6

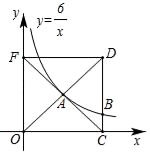
8．如图，双曲线的图象经过正方形对角线交点，则这条双曲线与正方形边交点的坐标为(　　)

A． B． C． D．

9．若成立，则下列不等式成立的是（    ）

A． B．

C． D．

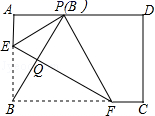
10．如图，在矩形ABCD中，点E，F分别在边AB，BC上，且AE=AB，将矩形沿直线EF折叠，点B恰好落在AD边上的点P处，连接BP交EF于点Q，对于下列结论：①EF=2BE；②PF=2PE；③FQ=4EQ；④△PBF是等边三角形．其中正确的是（ ）

A．①② B．②③ C．①③ D．①④

二、填空题(本大题共有6小题，每小题3分，共18分)

11．已知菱形的两条对角线长分别为1和4，则菱形的面积为______．

12．______．

13．在新年晚会的投飞镖游戏环节中，名同学的投掷成绩（单位：环）分别是：，，，，，，，则这组数据的众数是________．

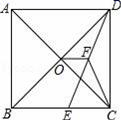
14．如图，在正方形ABCD中，对角线AC与BD相交于点O，E为BC上一点，CE=5，F为DE的中点．若OF的长为，则△CEF的周长为______．

15．一组数据﹣1，0，1，2，3的方差是_____．

16．已知，则的值等于________.

三、解下列各题(本大题共8小题，共72分)

17．（8分）如图，已知线段AC、BC，利用尺规作一点O，使得点O到点A、B、C的距离均相等．(保留作图痕迹，不写作法)

18．（8分）如图，平行四边形ABCD中，CG⊥AB于点G，∠ABF=45°，F在CD上，BF交CD于点E，连接AE，AE⊥AD．

(1)若BG=1，BC=，求EF的长度；

(2)求证：CE+BE=AB．

19．（8分）列方程解应用题：

某市今年进行水网升级，1月1日起调整居民用水价格，每立方米水费上涨，小丽家去年12月的水费是15元，而今年5月的水费则是30元．已知小丽家今年5月的用水量比去年12月的用水量多5m3，求该市今年居民用水的价格．

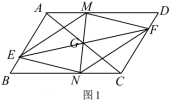
20．（8分）已知：如图1，在中，点为对角线的中点，过点的直线分别交边、于点、，过点的直线分别交边、于点、，且．

（1）求证：四边形为平行四边形；

（2）如图2，当四边形为矩形时，求证：．

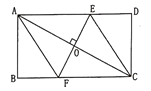
21．（8分）如图，矩形的对角线垂直平分线与边、分别交于点，求证：四边形为菱形.

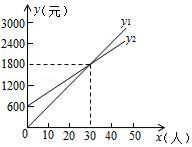
22．（10分）学校准备五一组织老师去隆中参加诸葛亮文化节，现有甲、乙两家旅行社表示对老师优惠，设参加文化节的老师有x人，甲、乙两家旅行社实际收费为y1、y2，且它们的函数图象如图所示，根据图象信息，请你回答下列问题：

（1）当参加老师的人数为多少时，两家旅行社收费相同？

（2）求出y1、y2关于x的函数关系式？

（3）如果共有50人参加时，选择哪家旅行社合算？

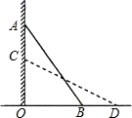
23．（10分）如图，一架梯子AB斜靠在一竖直的墙OA上，这时AO=2m，∠OAB=30°，梯子顶端A沿墙下滑至点C，使∠OCD=60°，同时，梯子底端B也外移至点D．求BD的长度．（结果保留根号）

24．（12分）已知某服装厂现有种布料70米，种布料52米，现计划用这两种布料生产、两种型号的时装共80套.已知做一套型号的时装需用A种布料1.1米，种布料0.4米，可获利50元；做一套型号的时装需用种布料0.6米，种布料0.9米，可获利45元.设生产型号的时装套数为，用这批布料生产两种型号的时装所获得的总利润为元.

（1）求（元）与（套）的函数关系式.

（2）有几种生产方案？

（3）如何生产使该厂所获利润最大？最大利润是多？

参考答案

一、选择题(每小题3分,共30分)

1、B

2、A

3、C

4、D

5、A

6、D

7、C

8、B

9、D

10、D

二、填空题(本大题共有6小题，每小题3分，共18分)

11、1

12、1

13、1

14、18

15、1

16、3

三、解下列各题(本大题共8小题，共72分)

17、见解析.

18、；证明见解析.

19、2.4元/米

20、（1）证明见解析；（2）证明见解析．

21、见解析

22、（1）当参加老师的人数为30时，两家旅行社收费相同；（2）y2＝40x+600；（3）如果共有50人参加时，选择乙家旅行社合算，理由见解析

23、米．

24、（1）y=5x+3600；（2）共有5种生产方案；（3）当生产型号的时装44套、生产型号的时装36套时，该厂所获利润最大，最大利润为3820元.