


上海市玉华中学2022-2023学年数学七年级第二学期期末达标检测模拟试题含答案
展开
这是一份上海市玉华中学2022-2023学年数学七年级第二学期期末达标检测模拟试题含答案,共6页。试卷主要包含了考生要认真填写考场号和座位序号,下列变形中,正确的是等内容,欢迎下载使用。
上海市玉华中学2022-2023学年数学七年级第二学期期末达标检测模拟试题(时间:120分钟 分数:120分) 学校_______ 年级_______ 姓名_______ 注意事项1.考生要认真填写考场号和座位序号。2.试题所有答案必须填涂或书写在答题卡上,在试卷上作答无效。第一部分必须用2B 铅笔作答;第二部分必须用黑色字迹的签字笔作答。3.考试结束后,考生须将试卷和答题卡放在桌面上,待监考员收回。 一、选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.如图,在▱ABCD中,连接AC,∠ABC=∠CAD=45°,AB=2,则BC的长是( )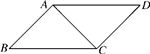 A.
A.![]() B.2 C.2
B.2 C.2![]() D.42.图①是我国古代著名的“赵爽弦图”的示意图,它是由四个全等的直角三角形围成的.若AC=6,BC=5,将四个直角三角形中的边长为6的直角边分别向外延长一倍,得到图②所示的“数学风车”,则这个风车的外围周长是( )
D.42.图①是我国古代著名的“赵爽弦图”的示意图,它是由四个全等的直角三角形围成的.若AC=6,BC=5,将四个直角三角形中的边长为6的直角边分别向外延长一倍,得到图②所示的“数学风车”,则这个风车的外围周长是( )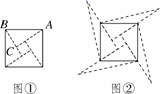 A.51 B.49 C.76 D.无法确定3.下列式子中,a取任何实数都有意义的是( )A.
A.51 B.49 C.76 D.无法确定3.下列式子中,a取任何实数都有意义的是( )A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 4.下列变形中,正确的是( )A.
4.下列变形中,正确的是( )A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 5.在我县“我的中国梦”演讲比赛中,有7名同学参加了比赛,他们最终决赛的成绩各不相同.其中一名学生想要知道自己是否进入前3名,不仅要知道自己的分数,还得知道这7名学生成绩的( )A.众数 B.方差 C.平均数 D.中位数6.如图,四边形ABCD是平行四边形,O是对角线AC与BD的交点,AB⊥AC,若AB=8,AC=12,则BD的长是( )
5.在我县“我的中国梦”演讲比赛中,有7名同学参加了比赛,他们最终决赛的成绩各不相同.其中一名学生想要知道自己是否进入前3名,不仅要知道自己的分数,还得知道这7名学生成绩的( )A.众数 B.方差 C.平均数 D.中位数6.如图,四边形ABCD是平行四边形,O是对角线AC与BD的交点,AB⊥AC,若AB=8,AC=12,则BD的长是( )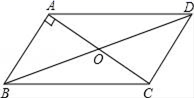 A.16 B.18 C.20 D.227.下面式子从左边到右边的变形属于因式分解的是( ).A.x2-x-2=x(x一1)-2 B.
A.16 B.18 C.20 D.227.下面式子从左边到右边的变形属于因式分解的是( ).A.x2-x-2=x(x一1)-2 B.![]() C.(x+1)(x—1)=x2 - 1 D.
C.(x+1)(x—1)=x2 - 1 D.![]() 8.某学校初、高六个年级共有
8.某学校初、高六个年级共有![]() 名学生,为了了解其视力情况,现采用抽样调查,如果按
名学生,为了了解其视力情况,现采用抽样调查,如果按![]() 的比例抽样,则样本容量是( )A.
的比例抽样,则样本容量是( )A.![]() B.
B.![]() C.
C.![]() D.
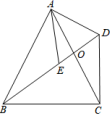
D.![]() 9.如图,在
9.如图,在![]() 中,
中,![]() ,点
,点![]() 是
是![]() 外一点,连接
外一点,连接![]() 、
、![]() 、
、![]() ,且
,且![]() 交
交![]() 于点
于点![]() ,在
,在![]() 上取一点
上取一点![]() ,使得
,使得![]() ,
,![]() .若
.若![]() ,则
,则![]() 的度数为
的度数为![]()
![]()
 A.
A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 10.平行四边形两个内角的度数的比是1:2,则其中较小的内角是( )A.
10.平行四边形两个内角的度数的比是1:2,则其中较小的内角是( )A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 11.若
11.若![]() ,则下列不等式成立的是( )A.
,则下列不等式成立的是( )A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 12.如果下列各组数是三角形的三边长,那么能组成直角三角形的一组数是( )A.
12.如果下列各组数是三角形的三边长,那么能组成直角三角形的一组数是( )A.![]() ,
,![]() ,
,![]() B.
B.![]() ,
,![]() ,
,![]() C.
C.![]() ,
,![]() ,
,![]() D.
D.![]() ,
,![]() ,
,![]() 二、填空题(每题4分,满分20分,将答案填在答题纸上)13.如图,折线ABC是某市在2018年乘出租车所付车费y(元)与行车里程x(km)之间的函数关系图像,观察图像回答,乘客在乘车里程超过3千米时,每多行驶1km,要再付费__________元.
二、填空题(每题4分,满分20分,将答案填在答题纸上)13.如图,折线ABC是某市在2018年乘出租车所付车费y(元)与行车里程x(km)之间的函数关系图像,观察图像回答,乘客在乘车里程超过3千米时,每多行驶1km,要再付费__________元.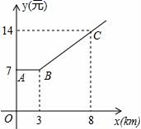 14.甲、乙两人各进行10次射击比赛,平均成绩均为9环,方差分别是:
14.甲、乙两人各进行10次射击比赛,平均成绩均为9环,方差分别是:![]() ,则射击成绩较稳定的是________(选填“甲”或“乙”).15.方程
,则射击成绩较稳定的是________(选填“甲”或“乙”).15.方程![]() =3的解是_____.16.如图,
=3的解是_____.16.如图,![]() 中,
中,![]() 是
是![]() 的中点,
的中点,![]() 平分
平分![]() ,
,![]() 于点
于点![]() ,若
,若![]() ,
,![]() ,则
,则![]() 的长度为_____.
的长度为_____.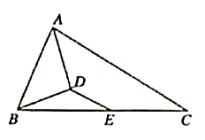 17.对于函数y=(m﹣2)x+1,若y随x的增大而增大,则m的取值范围_____.三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)18.(5分)化简与计算:(1)
17.对于函数y=(m﹣2)x+1,若y随x的增大而增大,则m的取值范围_____.三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)18.(5分)化简与计算:(1)![]() ;(2)
;(2)![]() ﹣x﹣1;(3)
﹣x﹣1;(3)![]() . 19.(5分)如图1,在△ABC中,AB=BC=5,AC=6,△ABC沿BC方向向右平移得△DCE,A、C对应点分别是D、E.AC与BD相交于点O.
. 19.(5分)如图1,在△ABC中,AB=BC=5,AC=6,△ABC沿BC方向向右平移得△DCE,A、C对应点分别是D、E.AC与BD相交于点O.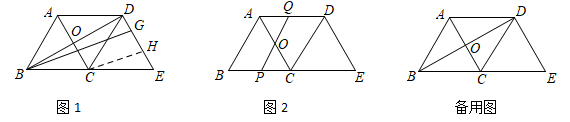 (1)将射线BD绕B点顺时针旋转,且与DC,DE分别相交于F,G,CH∥BG交DE于H,当DF=CF时,求DG的长;(2)如图2,将直线BD绕点O逆时针旋转,与线段AD,BC分别相交于点Q,P.设OQ=x,四边形ABPQ的周长为y,求y与x之间的函数关系式,并求y的最小值.(3)在(2)中PQ的旋转过程中,△AOQ是否构成等腰三角形?若能构成等腰三角形,求出此时PQ的长?若不能,请说明理由. 20.(8分)如图,
(1)将射线BD绕B点顺时针旋转,且与DC,DE分别相交于F,G,CH∥BG交DE于H,当DF=CF时,求DG的长;(2)如图2,将直线BD绕点O逆时针旋转,与线段AD,BC分别相交于点Q,P.设OQ=x,四边形ABPQ的周长为y,求y与x之间的函数关系式,并求y的最小值.(3)在(2)中PQ的旋转过程中,△AOQ是否构成等腰三角形?若能构成等腰三角形,求出此时PQ的长?若不能,请说明理由. 20.(8分)如图,![]() 是矩形
是矩形![]() 的边
的边![]() 延长线上的一点,连接
延长线上的一点,连接![]() ,交
,交![]() 于
于![]() ,把
,把![]() 沿
沿![]() 向左平移,使点
向左平移,使点![]() 与点
与点![]() 重合,
重合,![]() 吗?请说明理由.
吗?请说明理由.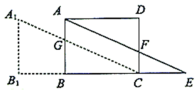 21.(10分)商场代售某品牌手机,原来每台的售价是3000元,一段时间后为了清库存,连续两次降价出售,现在的售价是1920元,求两次降价的平均降价率是多少? 22.(10分)如图,在
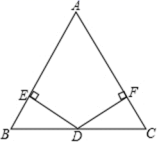
21.(10分)商场代售某品牌手机,原来每台的售价是3000元,一段时间后为了清库存,连续两次降价出售,现在的售价是1920元,求两次降价的平均降价率是多少? 22.(10分)如图,在![]() 中,
中,![]() ,点
,点![]() 是
是![]() 边上的中点,
边上的中点,![]() 、
、![]() 分别垂直
分别垂直![]() 、
、![]() 于点
于点![]() 和
和![]() .求证:
.求证:![]()
 23.(12分)(1)分解因式:
23.(12分)(1)分解因式:![]() ; (2)解方程:
; (2)解方程:![]() 参考答案 一、选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.1、C2、C3、A4、A5、D6、C7、B8、C9、C10、C11、B12、C 二、填空题(每题4分,满分20分,将答案填在答题纸上)13、1.114、甲15、116、1.17、m>1 三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)18、(1)﹣x﹣1;(2)
参考答案 一、选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.1、C2、C3、A4、A5、D6、C7、B8、C9、C10、C11、B12、C 二、填空题(每题4分,满分20分,将答案填在答题纸上)13、1.114、甲15、116、1.17、m>1 三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)18、(1)﹣x﹣1;(2)![]() ;(3)6﹣18
;(3)6﹣18![]() .19、(1)1;(1)y=1x+10(
.19、(1)1;(1)y=1x+10(![]() ≤x≤4),当x=
≤x≤4),当x=![]() 时,y有最小值,最小值为
时,y有最小值,最小值为![]() ;(3)能,满足条件的PQ的值为:
;(3)能,满足条件的PQ的值为:![]() 或2或3.20、见解析21、20%22、见解析23、(1)
或2或3.20、见解析21、20%22、见解析23、(1)![]() ;(2)原方程无解.
;(2)原方程无解.
相关试卷
这是一份上海市玉华中学2023-2024学年数学八上期末联考模拟试题含答案,共7页。试卷主要包含了下列图形中是轴对称图形的是,已知有意义,则的取值范围是,已知等内容,欢迎下载使用。
这是一份江西省育华学校2022-2023学年七年级数学第二学期期末达标检测模拟试题含答案,共7页。试卷主要包含了在下列命题中,是假命题的个数有等内容,欢迎下载使用。
这是一份江苏省无锡市玉祁初级中学2022-2023学年数学七年级第二学期期末达标检测模拟试题含答案,共7页。试卷主要包含了一组数据等内容,欢迎下载使用。









