


云南省普洱市名校2022-2023学年七下数学期末复习检测模拟试题含答案
展开云南省普洱市名校2022-2023学年七下数学期末复习检测模拟试题
(时间:120分钟 分数:120分)
学校_______ 年级_______ 姓名_______
请考生注意:
1.请用2B铅笔将选择题答案涂填在答题纸相应位置上,请用0.5毫米及以上黑色字迹的钢笔或签字笔将主观题的答案写在答题纸相应的答题区内。写在试题卷、草稿纸上均无效。
2.答题前,认真阅读答题纸上的《注意事项》,按规定答题。
一、选择题(每小题3分,共30分)
1.如图,在▱ABCD中,AB=3,AD=5,∠BCD的平分线交BA的延长线于点E,则AE的长为( )
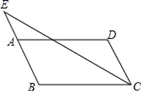
A.3 B.2.5 C.2 D.1.5
2.已知▱ABCD的周长为50cm,△ABC的周长为35cm,则对角线AC的长为( )
A.5cm B.10cm C.15cm D.20cm
3.下列各式中,正确的是( )
A.2<![]() <3 B.3<
<3 B.3<![]() <4 C.4<
<4 C.4<![]() <5 D.14<
<5 D.14<![]() <16
<16
4.我国是最早了解勾股定理的国家之一.下面四幅图中,不能用来证明勾股定理的是( )
A.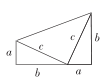 B.
B.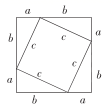 C.
C.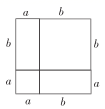 D.
D.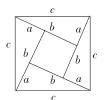
5.已知y=(k-3)x|k|-2+2是一次函数,那么k的值为( )
A.![]() B.3 C.
B.3 C.![]() D.无法确定
D.无法确定
6.如图,在平行四边形ABCD中,CE⊥AB,E为垂足.如果∠A=115°,则∠BCE=( )
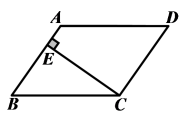
A.25° B.30° C.35° D.55°
7.如图,把Rt△ABC绕顶点C顺时针旋转90°得到Rt△DFC,若直线DF垂直平分AB,垂足为点E,连接BF,CE,且BC=2,下面四个结论:①BF=![]() ;②∠CBF=45°;③△BEC的面积=△FBC的面积;④△ECD的面积为
;②∠CBF=45°;③△BEC的面积=△FBC的面积;④△ECD的面积为![]() ,其中正确的结论有( )
,其中正确的结论有( )
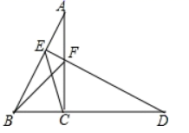
A.1个 B.2个 C.3个 D.4个
8.下列选项中,矩形具有的性质是( )
A.四边相等 B.对角线互相垂直 C.对角线相等 D.每条对角线平分一组对角
9.下列式子中,a取任何实数都有意义的是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
10.下列四个图形分别是四届国际数学家大会的会标,其中属于中心对称图形的有( )
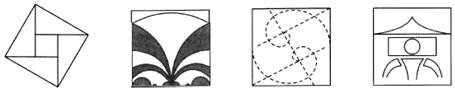
A.1个 B.2个 C.3个 D.4个
二、填空题(本大题共有6小题,每小题3分,共18分)
11.若分式![]() 的值为零,则x=___________。
的值为零,则x=___________。
12.若A(﹣1,y1)、B(﹣1,y1)在y=![]() 图象上,则y1、y1大小关系是y1_____y1.
图象上,则y1、y1大小关系是y1_____y1.
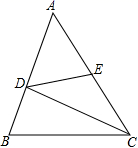
13.如图,在△ABC中,点D、E、F分别是BC、AB、AC的中点,如果△ABC的周长为20+2![]() ,那么△DEF的周长是_____.
,那么△DEF的周长是_____.
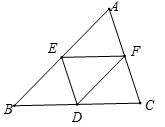
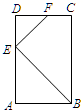
14.如图,在矩形纸片ABCD中,AB=12,BC=5,点E在AB上,将△DAE沿DE折叠,使点A落在对角线BD上的点A′处,则AE的长为 .
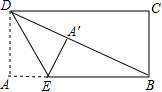
15.如图,在矩形ABCD中,∠BAD的平分线交BC于点E,交DC的延长线于点F,点G是EF的中点,连接CG、BG、BD、DG,下列结论:① BC=DF,②∠DGF=135o;③BG⊥DG,④ 若3AD=4AB,则4S△BDG=25S△DGF;正确的是____________(只填番号).
16.某工厂原计划在规定时间内生产12000个零件,实际每天比原计划多生产100个零件,结果比规定时间节省了![]() .若设原计划每天生产x个零件,则根据题意可列方程为_____.
.若设原计划每天生产x个零件,则根据题意可列方程为_____.
三、解下列各题(本大题共8小题,共72分)
17.(8分)如图,在![]() 中,E点为AC的中点,且有
中,E点为AC的中点,且有![]() ,
,![]() ,
,![]() ,
,![]() 求DE的长.
求DE的长.
18.(8分)某学校打算招聘英语教师。对应聘者进行了听、说、读、写的英语水平测试,其中甲、乙两名应聘者的成绩(百分制)如下表所示。

(1)如果学校想招聘说、读能力较强的英语教师,听、说、读、写成绩按照2:4:3:1的比确定,若在甲、乙两人中录取一人,请计算这两名应聘者的平均成绩(百分制)。从他们的成绩看,应该录取谁?
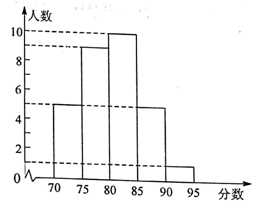
(2)学校按照(1)中的成绩计算方法,将所有应聘者的最后成绩绘制成如图所示的频数分布直方图(每组分数段均包含左端数值,不包含右端数值,如最后左边一组分数![]() 为:
为:![]() )。
)。
①参加该校本次招聘英语教师的应聘者共有______________人(直接写出答案即可)。
②学校决定由高分到低分录用3名教师,请判断甲、乙两人能否被录用?并说明理由。
19.(8分)某智能手机越来越受到大众的喜爱,各种款式相继投放市场,某店经营的A款手机去年销售总额为50000元,今年每部销售价比去年降低400元,若卖出的数量相同,销售总额将比去年减少20%.
已知A,B两款手机的进货和销售价格如下表:
| A款手机 | B款手机 |
进货价格(元) | 1100 | 1400 |
销售价格(元) | 今年的销售价格 | 2000 |
(1)今年A款手机每部售价多少元?
(2)该店计划新进一批A款手机和B款手机共90部,且B款手机的进货数量不超过A款手机数量的两倍,应如何进货才能使这批手机获利最多?
20.(8分)如图,在矩形ABCD中,AB=6,AD=12,点E在AD边上,且AE=8,EF⊥BE交CD于点F.
(1)求证:△ABE∽△DEF;
(2)求CF的长
21.(8分)阅读材料,解答问题:
有理化因式:两个含有根式的非零代数式相乘,如果它们的积不含有根式,那么这两个代数式相互叫做有理化因式.例如:![]() 的有理化因式是
的有理化因式是![]() ;1﹣
;1﹣![]() 的有理化因式是1+
的有理化因式是1+![]() .
.
分母有理化:分母有理化又称“有理化分母”,也就是把分母中的根号化去.指的是如果代数式中分母有根号,那么通常将分子、分母同乘以分母的有理化因式,达到化去分母中根号的目的.如:
![]() ﹣1,
﹣1,![]() .
.
请根据上述材料,计算:![]() 的值.
的值.
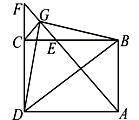
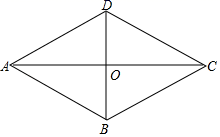
22.(10分)如图,在四边形ABCD中,AD∥BC,CA平分∠DCB,DB平分∠ADC
(1)求证:四边形ABCD是菱形;
(2)若AC=8,BD=6,求点D到AB的距离
23.(10分)已知a+b=5,ab=6,求多项式a3b+2a2b2+ab3的值.
24.(12分)已知x=2﹣![]() ,y=2+
,y=2+![]() ,求下列代数式的值
,求下列代数式的值
(1)x2+2xy+y2;
(2)![]()
![]()
参考答案
一、选择题(每小题3分,共30分)
1、C
2、B
3、B
4、C
5、C
6、A
7、C
8、C
9、A
10、B
二、填空题(本大题共有6小题,每小题3分,共18分)
11、1
12、>
13、10+![]()
14、![]()
15、①③④
16、![]()
![]() -
- ![]()
三、解下列各题(本大题共8小题,共72分)
17、DE=2.
18、(1)录取乙;(2)①30,②乙一定能被录用;甲不一定能被录用,见解析.
19、(1)今年A款手机每部售价1600元;(2)当新进A款手机30部,B款手机60部时,这批手机获利最大.
20、 (1)见详解;(2)![]() .
.
21、![]()
22、(1)见解析;(2)![]() .
.
23、1
24、(1)11;(2)1.
2023-2024学年云南省普洱市名校数学九上期末综合测试模拟试题含答案: 这是一份2023-2024学年云南省普洱市名校数学九上期末综合测试模拟试题含答案,共8页。试卷主要包含了答题时请按要求用笔等内容,欢迎下载使用。
云南省保山市名校2022-2023学年数学七下期末复习检测试题含答案: 这是一份云南省保山市名校2022-2023学年数学七下期末复习检测试题含答案,共7页。试卷主要包含了答题时请按要求用笔,下列式子为最简二次根式的是,一次函数的图象不经过等内容,欢迎下载使用。
2022-2023学年普洱市重点中学七下数学期末联考模拟试题含答案: 这是一份2022-2023学年普洱市重点中学七下数学期末联考模拟试题含答案,共5页。试卷主要包含了函数中,自变量x的取值范围是,使有意义的的取值范围是等内容,欢迎下载使用。












