


云南省昭通市巧家县2022-2023学年七年级数学第二学期期末学业质量监测试题含答案
展开
这是一份云南省昭通市巧家县2022-2023学年七年级数学第二学期期末学业质量监测试题含答案,共6页。
云南省昭通市巧家县2022-2023学年七年级数学第二学期期末学业质量监测试题(时间:120分钟 分数:120分) 学校_______ 年级_______ 姓名_______ 注意事项1.考试结束后,请将本试卷和答题卡一并交回.2.答题前,请务必将自己的姓名、准考证号用0.5毫米黑色墨水的签字笔填写在试卷及答题卡的规定位置.3.请认真核对监考员在答题卡上所粘贴的条形码上的姓名、准考证号与本人是否相符.4.作答选择题,必须用2B铅笔将答题卡上对应选项的方框涂满、涂黑;如需改动,请用橡皮擦干净后,再选涂其他答案.作答非选择题,必须用05毫米黑色墨水的签字笔在答题卡上的指定位置作答,在其他位置作答一律无效.5.如需作图,须用2B铅笔绘、写清楚,线条、符号等须加黑、加粗. 一、选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知m2-n2=mn,则![]() 的值等于( )A.1 B.0 C.-1 D.-
的值等于( )A.1 B.0 C.-1 D.-![]() 2.下列函数中,
2.下列函数中,![]() 是
是![]() 的正比例函数的是( )A.
的正比例函数的是( )A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 3.甲、乙、丙、丁四位选手各射击10次,每人的平均成绩都是9.3环,方差如表:选手
3.甲、乙、丙、丁四位选手各射击10次,每人的平均成绩都是9.3环,方差如表:选手
甲
乙
丙
丁
方差(环2)
0.035
0.016
0.022
0.025
则这四个人种成绩发挥最稳定的是( )A.甲 B.乙 C.丙 D.丁4.如图,在![]() 中,
中,![]() ,垂足为
,垂足为![]() ,
,![]() ,
,![]() ,则
,则![]() 的长为( )
的长为( )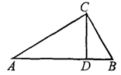 A.
A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 5.无论a取何值时,下列分式一定有意义的是( )A.
5.无论a取何值时,下列分式一定有意义的是( )A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 6.矩形ABCD的对角线AC,BD相交于点O,∠AOD=120°,AC=6,则△ABO的周长为( )A.18 B.15 C.12 D.97.用反证法证明“三角形中至少有一个内角大于或等于60°”时,应先假设( )A.有一个内角小于60° B.每一个内角都小于60°C.有一个内角大于60° D.每一个内角都大于60°8.若线段
6.矩形ABCD的对角线AC,BD相交于点O,∠AOD=120°,AC=6,则△ABO的周长为( )A.18 B.15 C.12 D.97.用反证法证明“三角形中至少有一个内角大于或等于60°”时,应先假设( )A.有一个内角小于60° B.每一个内角都小于60°C.有一个内角大于60° D.每一个内角都大于60°8.若线段![]() ,且点C是AB的黄金分割点,则BC等于( )A.
,且点C是AB的黄金分割点,则BC等于( )A.![]() B.
B.![]() C.
C.![]() 或
或![]() D.
D.![]() 或
或![]() 9.设四边形的内角和等于a,五边形的外角和等于b,则a与b的关系是( )A.a>b B.a=b C.a<b D.b=a+180°10.下列函数中,表示y是x的正比例函数的是( )A.y=﹣0.1x B.y=2x2 C.y2=4x D.y=2x+111.对于函数y=﹣5x+1,下列结论:①它的图象必经过点(﹣1,5)②它的图象经过第一、二、三象限③当x>1时,y<0④y的值随x值的增大而增大,其中正确的个数是( )A.0 B.1 C.2 D.312.如图,2002年8月在北京召开的国际数学家大会会徽取材于我国古代数学家赵爽的《勾股圆方图》(也称《赵爽弦图》),它是由四个全等的直角三角形与中间的一个小正方形拼成的一个大正方形,如图所示,如果大正方形的面积是13,小正方形的面积是1,直角三角形的短直角边为a,较长直角边为b,那么
9.设四边形的内角和等于a,五边形的外角和等于b,则a与b的关系是( )A.a>b B.a=b C.a<b D.b=a+180°10.下列函数中,表示y是x的正比例函数的是( )A.y=﹣0.1x B.y=2x2 C.y2=4x D.y=2x+111.对于函数y=﹣5x+1,下列结论:①它的图象必经过点(﹣1,5)②它的图象经过第一、二、三象限③当x>1时,y<0④y的值随x值的增大而增大,其中正确的个数是( )A.0 B.1 C.2 D.312.如图,2002年8月在北京召开的国际数学家大会会徽取材于我国古代数学家赵爽的《勾股圆方图》(也称《赵爽弦图》),它是由四个全等的直角三角形与中间的一个小正方形拼成的一个大正方形,如图所示,如果大正方形的面积是13,小正方形的面积是1,直角三角形的短直角边为a,较长直角边为b,那么![]() 的值为( )
的值为( )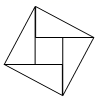 A.13 B.19 C.25 D.169二、填空题(每题4分,满分20分,将答案填在答题纸上)13.如图,每一幅图中均含有若干个正方形,第1幅图中有1个正方形;第2幅图中有1+4=5个正方形;第三幅图中有1+4+9=14个正方形;…按这样的规律下去,第4幅图中有_____个正方形.
A.13 B.19 C.25 D.169二、填空题(每题4分,满分20分,将答案填在答题纸上)13.如图,每一幅图中均含有若干个正方形,第1幅图中有1个正方形;第2幅图中有1+4=5个正方形;第三幅图中有1+4+9=14个正方形;…按这样的规律下去,第4幅图中有_____个正方形.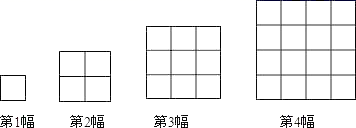 14.若n边形的每个内角都等于150°,则n=_____.15.如图,菱形
14.若n边形的每个内角都等于150°,则n=_____.15.如图,菱形![]() 中,
中,![]() 垂直平分
垂直平分![]() ,垂足为
,垂足为![]() ,
,![]() .那么菱形
.那么菱形![]() 的对角线
的对角线![]() 的长是_____
的长是_____![]() .
.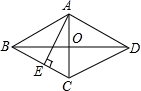 16.如图,△A1OM是腰长为1的等腰直角三角形,以A1M为一边,作A1A2⊥A1M,且A1A2=1,连接A2M,再以A2M为一边,作A2A3⊥A2M,且A2A3=1,则A1M=_____,照此规律操作下去…则AnM=_____.
16.如图,△A1OM是腰长为1的等腰直角三角形,以A1M为一边,作A1A2⊥A1M,且A1A2=1,连接A2M,再以A2M为一边,作A2A3⊥A2M,且A2A3=1,则A1M=_____,照此规律操作下去…则AnM=_____.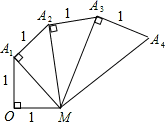 17.如图,在
17.如图,在![]() 中,
中,![]() ,
,![]() ,点D在边
,点D在边![]() 上,若以
上,若以![]() 、
、![]() 为边,以
为边,以![]() 为对角线,作
为对角线,作![]() ,则对角线
,则对角线![]() 的最小值为_______.
的最小值为_______.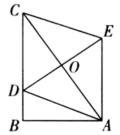 三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)18.(5分)如图,在平面直角坐标系xOy中,一次函数
三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)18.(5分)如图,在平面直角坐标系xOy中,一次函数![]() 的图象与正比例函数
的图象与正比例函数![]() 的图象交于点A(2,m),一次函数
的图象交于点A(2,m),一次函数![]() 的图象分别与x轴、y轴交于B、C两点.(1)求m、k的值;(2)求∠ACO的度数和线段AB的长.
的图象分别与x轴、y轴交于B、C两点.(1)求m、k的值;(2)求∠ACO的度数和线段AB的长.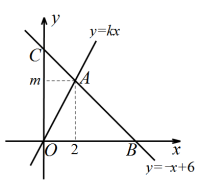 19.(5分)已知求代数式:x=2+
19.(5分)已知求代数式:x=2+![]() ,y=2-
,y=2-![]() .(1)求代数式x2+3xy+y2的值;(2)若一个菱形的对角线的长分别是x和y,求这个菱形的面积? 20.(8分)甲、乙两人分别骑自行车和摩托车沿相同路线由A地到相距80千米的B地,行驶过程中的函数图像如图所示。
.(1)求代数式x2+3xy+y2的值;(2)若一个菱形的对角线的长分别是x和y,求这个菱形的面积? 20.(8分)甲、乙两人分别骑自行车和摩托车沿相同路线由A地到相距80千米的B地,行驶过程中的函数图像如图所示。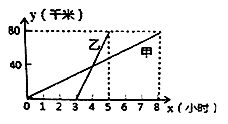 (1)请根据图像回答下列问题:甲先出发 小时后,乙才出发;在甲出发 小时后两人相遇,这时他们距A地 千米;(2)乙的行驶速度 千米/小时;(3)分别求出甲、乙在行驶过程中的路程(千米)与时间(小时)之间的函数关系式(不要求写出自变量的取值范围)。 21.(10分)如图,已知点A(﹣2,0),点B(6,0),点C在第一象限内,且△OBC为等边三角形,直线BC交y轴于点D,过点A作直线AE⊥BD于点E,交OC于点E
(1)请根据图像回答下列问题:甲先出发 小时后,乙才出发;在甲出发 小时后两人相遇,这时他们距A地 千米;(2)乙的行驶速度 千米/小时;(3)分别求出甲、乙在行驶过程中的路程(千米)与时间(小时)之间的函数关系式(不要求写出自变量的取值范围)。 21.(10分)如图,已知点A(﹣2,0),点B(6,0),点C在第一象限内,且△OBC为等边三角形,直线BC交y轴于点D,过点A作直线AE⊥BD于点E,交OC于点E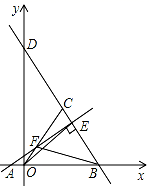 (1)求直线BD的解析式;(2)求线段OF的长;(3)求证:BF=OE. 22.(10分)温度的变化是人们经常谈论的话题,请根据下图解决下列问题.
(1)求直线BD的解析式;(2)求线段OF的长;(3)求证:BF=OE. 22.(10分)温度的变化是人们经常谈论的话题,请根据下图解决下列问题.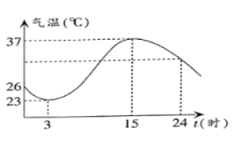 (1)这一天的最高温度是多少?是在几时到达的?(2)这一天的温差是多少?从最低温度到最高温度经过多长时间?(3)在什么时间范围内温度在上升?在什么时间范围内温度在下降? 23.(12分)阅读材料:在实数范围内,当
(1)这一天的最高温度是多少?是在几时到达的?(2)这一天的温差是多少?从最低温度到最高温度经过多长时间?(3)在什么时间范围内温度在上升?在什么时间范围内温度在下降? 23.(12分)阅读材料:在实数范围内,当![]() 且
且![]() 时 ,我们由非负数的性质知道
时 ,我们由非负数的性质知道![]() ,所以
,所以![]() , 即:
, 即:![]() ,当且仅当
,当且仅当![]() =
=![]() 时,等号成立,这就是数学上有名的“均值不等式”,若
时,等号成立,这就是数学上有名的“均值不等式”,若![]() 与
与![]() 的积为定值
的积为定值![]() . 则
. 则![]() 有最小值
有最小值![]() :请问: 若
:请问: 若 ![]() , 则当
, 则当![]() 取何值时,代数式
取何值时,代数式![]() 取最小值? 最小值是多少? 参考答案 一、选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.1、C2、A3、B4、A5、D6、D7、B8、D9、B10、A11、B12、C 二、填空题(每题4分,满分20分,将答案填在答题纸上)13、114、115、
取最小值? 最小值是多少? 参考答案 一、选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.1、C2、A3、B4、A5、D6、D7、B8、D9、B10、A11、B12、C 二、填空题(每题4分,满分20分,将答案填在答题纸上)13、114、115、![]() 16、
16、![]()
![]() . 17、1 三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)18、(1)m=4,k=2;(2)∠ACO=45°,AB
. 17、1 三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)18、(1)m=4,k=2;(2)∠ACO=45°,AB![]() .19、(1)18;(2)1.20、(1)3,4,40 (2)40 (3)y=40x-12021、(1)
.19、(1)18;(2)1.20、(1)3,4,40 (2)40 (3)y=40x-12021、(1)![]() ;(1)OF= 1;(3)见解析.22、(1)这一天的最高温度是37℃,是在15时到达的;(2)温差为
;(1)OF= 1;(3)见解析.22、(1)这一天的最高温度是37℃,是在15时到达的;(2)温差为![]() ,经过的时间为
,经过的时间为![]() 时;(3)从3时到15时温度在上升,在0时到3时、15时到24时温度在下降.23、x=2时,最小值是1.
时;(3)从3时到15时温度在上升,在0时到3时、15时到24时温度在下降.23、x=2时,最小值是1.
相关试卷
这是一份2023-2024学年云南省昭通市盐津县数学九上期末学业质量监测试题含答案,共8页。试卷主要包含了考生必须保证答题卡的整洁,下列函数是二次函数的是等内容,欢迎下载使用。
这是一份2023-2024学年云南省昭通市名校数学九上期末学业质量监测模拟试题含答案,共7页。
这是一份云南省昭通市盐津县2023-2024学年数学九上期末学业质量监测试题含答案,共9页。试卷主要包含了考生必须保证答题卡的整洁,下列多边形一定相似的是等内容,欢迎下载使用。









