包头市重点中学2022-2023学年数学七年级第二学期期末检测模拟试题含答案

包头市重点中学2022-2023学年数学七年级第二学期期末检测模拟试题

（时间：120分钟             分数：120分）

学校_______            年级_______        姓名_______

注意事项：

1．答卷前，考生务必将自己的姓名、准考证号填写在答题卡上。

2．回答选择题时，选出每小题答案后，用铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其它答案标号。回答非选择题时，将答案写在答题卡上，写在本试卷上无效。

3．考试结束后，将本试卷和答题卡一并交回。

一、选择题(每小题3分,共30分)

1．下列对二次函数y=x2﹣x的图象的描述，正确的是（　　）

A．开口向下 B．对称轴是y轴

C．经过原点 D．在对称轴右侧部分是下降的

2．如图，在正方形ABCD外侧，作等边三角形ADE，AC，BE相交于点F，则∠BFC为（　　）

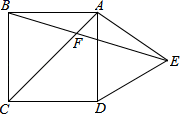
A．75° B．60° C．55° D．45°

3．如图，在▱ABCD 中，若∠A+∠C=130°，则∠D 的大小为（    ）

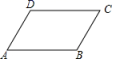
A．100° B．105° C．110° D．115°

4．若代数式在实数范围内有意义，则x的取值范围是（　　）

A．x＜3 B．x≤3 C．x＞3 D．x≥3

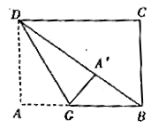
5．如图所示，在矩形纸片中，，，折叠纸片使边与对角线重合，点落在点处，折痕为，则的长为(    )

A． B． C． D．

6．已知点在直线上，则关于的不等式的解集是(　　)

A． B． C． D．

7．如图，甲、丙两地相距500km，一列快车从甲地驶往丙地，途中经过乙地；一列慢车从乙地驶往丙地，两车同时出发，同向而行，折线ABCD表示两车之间的距离y(km)与慢车行驶的时间为x(h)之间的函数关系．根据图中提供的信息，下列说法不正确的是(　　)

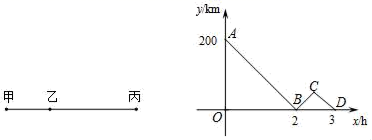
A．甲、乙两地之间的距离为200 km B．快车从甲地驶到丙地共用了2.5 h

C．快车速度是慢车速度的1.5倍 D．快车到达丙地时，慢车距丙地还有50 km

8．某储运部紧急调拨一批物资，调进物资共用４小时，调进物资2小时后开始调出物资（调进物资与调出物资的速度均保持不变）．储运部库存物资S(吨)与时间t(小时)之间的函数关系如图所示，这批物资从开始调进到全部调出需要的时间是（    ）

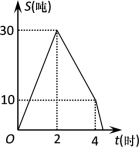
A．4小时 B．4.4小时 C．4.8小时 D．5小时

9．根据二次函数y＝－x2＋2x＋3的图像，判断下列说法中，错误的是（ ）

A．二次函数图像的对称轴是直线x＝1；

B．当x＞0时，y＜4；

C．当x≤1时，函数值y是随着x的增大而增大；

D．当y≥0时，x的取值范围是－1≤x≤3时．

10．要使代数式有意义，则的取值范围是（  ）

A． B． C． D．且

二、填空题(本大题共有6小题，每小题3分，共18分)

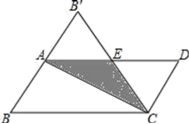
11．如图，在平行四边形纸片ABCD中，AB＝3，将纸片沿对角线AC对折，BC边与AD边交于点E，此时，△CDE恰为等边三角形，则图中重叠部分的面积为_____．

12．一组数据1，2，a，4，5的平均数是3，则这组数据的方差为_____．

13．已知矩形，给出三个关系式：①②③如果选择关系式__________作为条件（写出一个即可），那么可以判定矩形为正方形，理由是_______________________________ .

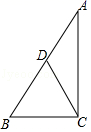
14．如图，Rt△ABC中，∠ACB=90°，AB=6，D是AB的中点，则CD=_____．

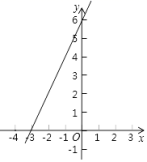
15．一次函数y=kx+b的图象如图所示，则不等式kx+b<0的解集为__________．

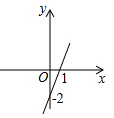
16．一次函数y=2x+6的图象如图所示，则不等式2x+6＞0的解集是________，当y≤3时，x的取值范围是________． 

三、解下列各题(本大题共8小题，共72分)

17．（8分）学校通过初评决定最后从甲、乙、丙三个班中推荐一个班为县级先进班集体，下表是三个班的五项素质考评得分表。

五项素质考评得分表（单位：分）

根据统计表中的信息回答下列问题：

（1）请你补全五项成绩考评分析表中的数据：

（2）参照上表中的数据，你推荐哪个班为县级先进班集体？并说明理由。

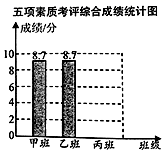
（3）如果学校把行为规范、学习成绩、校运动会、艺术获奖、劳动卫生五项考评成绩按照3∶2∶1∶1∶3的比确定班级的综合成绩，学生处的李老师根据这个综合成绩，绘制了一幅不完整的条形统计图，请将这个统计图补充完整，按照这个成绩，应推荐哪个班为县级先进班集体？为什么？

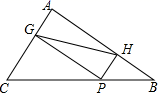
18．（8分）如图，在△ABC中，AC=9，AB=12，BC=15，P为BC边上一动点，PG⊥AC于点G，PH⊥AB于点H．

(1)求证：四边形AGPH是矩形；

(2)在点P的运动过程中，GH的长度是否存在最小值？若存在，请求出最小值，若不存在，请说明理由．

19．（8分）有红、白、蓝三种颜色的小球各一个，它们除颜色外没有其他任何区别.现将3个小球放入编号为①②③的三个盘子里，规定每个盒子里放一个，且只能放一个小球

（1）请用树状图或其他适当的形式列举出3个小球放入盒子的所有可能情况；

（2）求红球恰好被放入②号盒子的概率.

20．（8分）如图，△ABC中，CD平分∠ACB，CD的垂直平分线分别交AC、DC、BC

于点E、F、G，连接DE、DG．

(1)求证：四边形DGCE是菱形；

(2)若∠ACB=30°，∠B=45°，CG=10，求BG的长．

21．（8分）由于受到手机更新换代的影响，某店经销的甲型号手机今年的售价比去年每台降价500元．如果卖出相同数量的手机，那么去年销售额为8万元，今年销售额只有6万元．

（1）今年甲型号手机每台售价为多少元？

（2）为了提高利润，该店计划购进乙型号手机销售，已知甲型号手机每台进价为1000元，乙型号手机每台进价为800元，预计用不多于1.84万元且不少于1.76万元的资金购进这两种手机共20台，请问有几种进货方案？

22．（10分）阅读材料： 小明在学习二次根式后，发现一些含根号的式子可以写成另一个式子的平方，如：，善于思考的小明进行了以下探索：

设（其中均为整数），则有．

∴．这样小明就找到了一种把部分的式子化为平方式的方法．

请你仿照小明的方法探索并解决下列问题：

当均为正整数时，若，用含m、n的式子分别表示，得＝　   　，＝　   　；

（2）利用所探索的结论，找一组正整数，填空：   ＋　 　＝(　 　＋　 　)2；

（3）若，且均为正整数，求的值．

23．（10分）如图，四边形是正方形，是边所在直线上的点，，且交正方形外角的平分线于点.

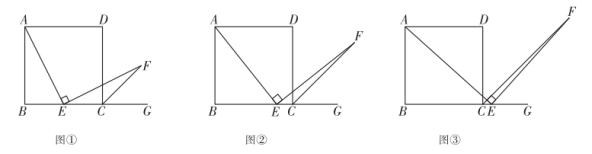
（1）当点在线段中点时（如图①），易证，不需证明；

（2）当点在线段上（如图②）或在线段延长线上（如图③）时，（1）中的结论是否仍然成立？请写出你的猜想，并选择图②或图③的一种结论给予证明.

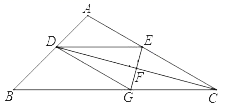
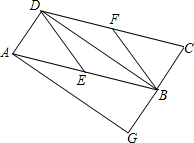
24．（12分）已知：如图，在平行四边形ABCD中，E、F分别为边AB、CD的中点，BD是对角线，AG∥DB交CB的延长线于G．

(1)求证：△ADE≌△CBF；

(2)若四边形BEDF是菱形，则四边形AGBD是什么特殊四边形？并证明你的结论．

参考答案

一、选择题(每小题3分,共30分)

1、C

2、B

3、D

4、B

5、D

6、C

7、C

8、B

9、B

10、B

二、填空题(本大题共有6小题，每小题3分，共18分)

11、．

12、1

13、①    一组邻边相等的矩形是正方形   

14、1

15、x<1

16、x＞﹣3    x≤﹣   

三、解下列各题(本大题共8小题，共72分)

17、（1）8.6，8，10；（2）甲班：三个班的平均数相同，甲班众数与中位数高于乙和丙；（3）画图见解析，丙班.

18、 (1)证明见解析；(2)见解析.

19、（1）详见解析；（2）

20、 (1)证明见解析；(2)BG= 5+5．

21、（1）今年甲型号手机每台售价为1元；（2）共有5种进货方案．

22、（1），；（2）2，2，1，1（答案不唯一）；（3）＝7或＝1．

23、（1）见解析；（2）成立，理由见解析.

24、（1）证明见解析（2）当四边形BEDF是菱形时，四边形AGBD是矩形；证明见解析；