


北京市延庆区2022-2023学年数学七年级第二学期期末达标测试试题含答案
展开
这是一份北京市延庆区2022-2023学年数学七年级第二学期期末达标测试试题含答案,共8页。试卷主要包含了平行四边形具有的特征是等内容,欢迎下载使用。
北京市延庆区2022-2023学年数学七年级第二学期期末达标测试试题(时间:120分钟 分数:120分) 学校_______ 年级_______ 姓名_______ 注意事项:1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其它答案标号。回答非选择题时,将答案写在答题卡上,写在本试卷上无效。3.考试结束后,将本试卷和答题卡一并交回。 一、选择题(每小题3分,共30分)1.如果点A(﹣2,a)在函数y![]() x+3的图象上,那么a的值等于( )A.﹣7 B.3 C.﹣1 D.42.下列函数的图象经过
x+3的图象上,那么a的值等于( )A.﹣7 B.3 C.﹣1 D.42.下列函数的图象经过![]()
![]() ,且
,且![]() 随
随![]() 的增大而减小的是( )A.
的增大而减小的是( )A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 3.如图,线段
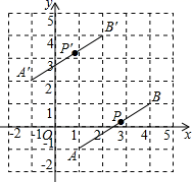
3.如图,线段![]() 经过平移得到线段
经过平移得到线段![]() ,其中点
,其中点![]() ,
,![]() 的对应点分别为点
的对应点分别为点![]() ,
,![]() ,这四个点都在格点上.若线段
,这四个点都在格点上.若线段![]() 上有一个点
上有一个点![]()
![]() ,
,![]() ,则点
,则点![]() 在
在![]() 上的对应点
上的对应点![]() 的坐标为
的坐标为![]()
![]()
 A.
A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 4.下列各式中,不是最简二次根式的是( )A.
4.下列各式中,不是最简二次根式的是( )A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 5.实数 x 取任何值,下列代数式都有意义的是( )A.
5.实数 x 取任何值,下列代数式都有意义的是( )A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 6.平行四边形具有的特征是( )A.四个角都是直角 B.对角线相等C.对角线互相平分 D.四边相等7.已知二次根式
6.平行四边形具有的特征是( )A.四个角都是直角 B.对角线相等C.对角线互相平分 D.四边相等7.已知二次根式![]() 的值为3,那么
的值为3,那么![]() 的值是( )A.3 B.9 C.-3 D.3或-38.如图,△ABC中,D、E分别是AB、AC边的中点,延长DE至F,使EF=
的值是( )A.3 B.9 C.-3 D.3或-38.如图,△ABC中,D、E分别是AB、AC边的中点,延长DE至F,使EF=![]() DF,若BC=8,则DF的长为( )
DF,若BC=8,则DF的长为( ) A.6 B.8 C.4 D.
A.6 B.8 C.4 D.![]() 9.如果三条线段a、b、c满足a2=(c+b)(c﹣b),那么这三条线段组成的三角形是( )A.直角三角形 B.锐角三角形 C.钝角三角形 D.不能确定10.若x>y,则下列不等式中不一定成立的是( )A.x﹣1>y﹣1 B.2x>2y C.x+1>y+1 D.x2>y2二、填空题(本大题共有6小题,每小题3分,共18分)11.如图,在
9.如果三条线段a、b、c满足a2=(c+b)(c﹣b),那么这三条线段组成的三角形是( )A.直角三角形 B.锐角三角形 C.钝角三角形 D.不能确定10.若x>y,则下列不等式中不一定成立的是( )A.x﹣1>y﹣1 B.2x>2y C.x+1>y+1 D.x2>y2二、填空题(本大题共有6小题,每小题3分,共18分)11.如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分别为
分别为![]() ,
,![]() ,
,![]() 的中点,
的中点,![]() ,则
,则![]() 的长度为__.
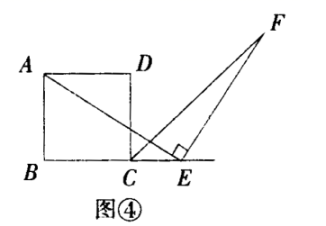
的长度为__.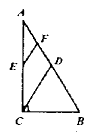 12.两个相似三角形最长边分别为10cm和25cm,它们的周长之差为60cm,则这两个三角形的周长分别是。13.在一个不透明的布袋中,红色、黑色的玻璃球共有20个,这些球除颜色外其它完全相同.将袋中的球搅匀,从中随机摸出一个球,记下颜色后再放回袋中,不断地重复这个过程,摸了200次后,发现有60次摸到黑球,请你估计这个袋中红球约有_____个.14.如图,在△ABC中,∠ACB=90°,D、E、F分别是AC、AB、BC的中点,CE=3,则DF_____.
12.两个相似三角形最长边分别为10cm和25cm,它们的周长之差为60cm,则这两个三角形的周长分别是。13.在一个不透明的布袋中,红色、黑色的玻璃球共有20个,这些球除颜色外其它完全相同.将袋中的球搅匀,从中随机摸出一个球,记下颜色后再放回袋中,不断地重复这个过程,摸了200次后,发现有60次摸到黑球,请你估计这个袋中红球约有_____个.14.如图,在△ABC中,∠ACB=90°,D、E、F分别是AC、AB、BC的中点,CE=3,则DF_____.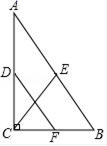 15.已知
15.已知![]() ,则比较大小2
,则比较大小2![]() _____3
_____3![]() (填“<“或“>”)16.已知函数y=3x的图象经过点A(-1,y1),点B(-2,y2),则y1____y2(填“>”或“<”或“=”).三、解下列各题(本大题共8小题,共72分)17.(8分)某机动车出发前油箱内有油42L,行驶若干小时后,在途中加油站加油若干升.油箱中余油量Q(L)与行驶时间t(h)之间的函数关系如图所示,根据如图回答问题:
(填“<“或“>”)16.已知函数y=3x的图象经过点A(-1,y1),点B(-2,y2),则y1____y2(填“>”或“<”或“=”).三、解下列各题(本大题共8小题,共72分)17.(8分)某机动车出发前油箱内有油42L,行驶若干小时后,在途中加油站加油若干升.油箱中余油量Q(L)与行驶时间t(h)之间的函数关系如图所示,根据如图回答问题: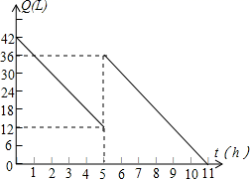 (1)机动车行驶几小时后加油?加了多少油?(2)请求出加油前油箱余油量Q与行驶时间t之间的关系式;(3)如果加油站离目的地还有230km,车速为40km/h,要到达目的地,油箱中的油是否够用?请说明理由. 18.(8分)如图①,四边形
(1)机动车行驶几小时后加油?加了多少油?(2)请求出加油前油箱余油量Q与行驶时间t之间的关系式;(3)如果加油站离目的地还有230km,车速为40km/h,要到达目的地,油箱中的油是否够用?请说明理由. 18.(8分)如图①,四边形![]() 是正方形,点
是正方形,点![]() 是边
是边![]() 的中点,
的中点,![]() ,且
,且![]() 交正方形的外角平分线
交正方形的外角平分线![]() 于点
于点![]() 请你认真阅读下面关于这个图形的探究片段,完成所提出的问题.
请你认真阅读下面关于这个图形的探究片段,完成所提出的问题. (1)探究1:小强看到图①后,很快发现
(1)探究1:小强看到图①后,很快发现![]() 这需要证明AE和EF所在的两个三角形全等,但△ABE和△ECF显然不全等(个直角三角形,一个钝角三角形)考虑到点E是边BC的中点,因此可以选取AB的中点M(如图②),连接EM后尝试着去证明
这需要证明AE和EF所在的两个三角形全等,但△ABE和△ECF显然不全等(个直角三角形,一个钝角三角形)考虑到点E是边BC的中点,因此可以选取AB的中点M(如图②),连接EM后尝试着去证明![]() 就行了.随即小强写出了如下的证明过程:证明:如图②,取AB的中点M,连接EM.∵
就行了.随即小强写出了如下的证明过程:证明:如图②,取AB的中点M,连接EM.∵![]() ∴
∴![]() 又∵
又∵![]() ∴
∴![]() ∵点E、M分别为正方形的边BC和AB的中点,∴
∵点E、M分别为正方形的边BC和AB的中点,∴![]() ∴
∴![]() 是等腰直角三角形,
是等腰直角三角形,![]() ∴
∴![]() 又∵
又∵![]() 是正方形外角的平分线,∴
是正方形外角的平分线,∴![]() ,∴
,∴![]() ∴
∴![]() ∴
∴![]() ,∴
,∴![]() (2)探究2:小强继续探索,如图③,若把条件“点E是边BC的中点”改为“点E是边BC上的任意一点”,其余条件不变,发现AE=EF仍然成立小强进一步还想试试,如图④,若把条件“点E是边BC的中点”为“点E是边BC延长线上的一点”,其余条件仍不变,那么结论AE=EF仍然成立请你选择图③或图④中的一种情况写出证明过程给小强看.
(2)探究2:小强继续探索,如图③,若把条件“点E是边BC的中点”改为“点E是边BC上的任意一点”,其余条件不变,发现AE=EF仍然成立小强进一步还想试试,如图④,若把条件“点E是边BC的中点”为“点E是边BC延长线上的一点”,其余条件仍不变,那么结论AE=EF仍然成立请你选择图③或图④中的一种情况写出证明过程给小强看.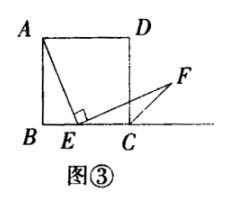
 19.(8分)如图,E,F是平行四边形ABCD的对角线AC上的点,CE=AF.请你猜想:BE与DF有怎样的位置关系和数量关系?并对你的猜想加以证明.
19.(8分)如图,E,F是平行四边形ABCD的对角线AC上的点,CE=AF.请你猜想:BE与DF有怎样的位置关系和数量关系?并对你的猜想加以证明.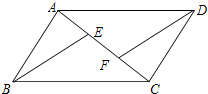 20.(8分)已知关于
20.(8分)已知关于![]() 的一次函数
的一次函数![]() ,求满足下列条件的m的取值范围:(1)函数值y 随x的增大而增大;(2)函数图象与y 轴的负半轴相交;(3)函数的图象过原点. 21.(8分)先化简,再求值:(x+2)2﹣4x(x+1),其中x=
,求满足下列条件的m的取值范围:(1)函数值y 随x的增大而增大;(2)函数图象与y 轴的负半轴相交;(3)函数的图象过原点. 21.(8分)先化简,再求值:(x+2)2﹣4x(x+1),其中x=![]() . 22.(10分)在平面直角坐标系内,已知
. 22.(10分)在平面直角坐标系内,已知![]() .
.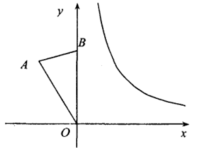 (1)点A的坐标为(____,______);(2)将
(1)点A的坐标为(____,______);(2)将![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 度
度![]() .①当
.①当![]() 时,点
时,点![]() 恰好落在反比例函数
恰好落在反比例函数![]()
![]() 的图象上,求
的图象上,求![]() 的值;②在旋转过程中,点
的值;②在旋转过程中,点![]() 能否同时落在上述反比例函数的图象上,若能,求出
能否同时落在上述反比例函数的图象上,若能,求出![]() 的值;若不能,请说明理由. 23.(10分)如图,在正方形纸片ABCD中,对角线AC、BD交于点O,折叠正方形纸片ABCD,使AD落在BD上,点A恰好与BD上的点F重合,展开后,折叠DE分别交AB、AC于E、G,连接GF,下列结论:①∠FGD=112.5°②BE=2OG③S△AGD=S△OGD④四边形AEFG是菱形( )
的值;若不能,请说明理由. 23.(10分)如图,在正方形纸片ABCD中,对角线AC、BD交于点O,折叠正方形纸片ABCD,使AD落在BD上,点A恰好与BD上的点F重合,展开后,折叠DE分别交AB、AC于E、G,连接GF,下列结论:①∠FGD=112.5°②BE=2OG③S△AGD=S△OGD④四边形AEFG是菱形( ) A.1个 B.2个 C.3个 D.4个 24.(12分)如图,在正方形
A.1个 B.2个 C.3个 D.4个 24.(12分)如图,在正方形![]() 中,点
中,点![]() 、
、![]() 是正方形内两点,
是正方形内两点,![]() ,
,![]() ,为探索这个图形的特殊性质,某数学兴趣小组经历了如下过程:
,为探索这个图形的特殊性质,某数学兴趣小组经历了如下过程: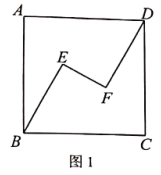 (1)在图1中,连接
(1)在图1中,连接![]() ,且
,且![]() ①求证:
①求证:![]() 与
与![]() 互相平分;②求证:
互相平分;②求证:![]() ;(2)在图2中,当
;(2)在图2中,当![]() ,其它条件不变时,
,其它条件不变时,![]() 是否成立?若成立,请证明:若不成立,请说明理由.
是否成立?若成立,请证明:若不成立,请说明理由.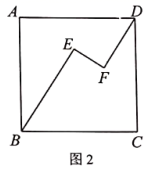 (3)在图3中,当
(3)在图3中,当![]() ,
,![]() ,
,![]() 时,求
时,求![]() 之长.
之长.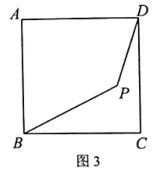 参考答案 一、选择题(每小题3分,共30分)1、D2、D3、A4、A5、C6、C7、D8、A9、A10、D 二、填空题(本大题共有6小题,每小题3分,共18分)11、612、40cm,100cm13、114、=315、<16、> 三、解下列各题(本大题共8小题,共72分)17、(1)5小时, 24L;(2)Q=42-6t;(3)见解析.18、见解析19、BE∥DF,BE=DF,理由见解析20、(1)
参考答案 一、选择题(每小题3分,共30分)1、D2、D3、A4、A5、C6、C7、D8、A9、A10、D 二、填空题(本大题共有6小题,每小题3分,共18分)11、612、40cm,100cm13、114、=315、<16、> 三、解下列各题(本大题共8小题,共72分)17、(1)5小时, 24L;(2)Q=42-6t;(3)见解析.18、见解析19、BE∥DF,BE=DF,理由见解析20、(1)![]() ,(2)
,(2)![]() ,(3)
,(3)![]() 21、原式=﹣3x1+4,当x=
21、原式=﹣3x1+4,当x=![]() 时,原式=﹣1.22、(1)A(-1,
时,原式=﹣1.22、(1)A(-1,![]() );(2)①
);(2)①![]() ;②
;②![]() ,理由见解析23、C24、(1)①详见解析;②详见解析;(1)当BE≠DF时,(BE+DF)1+EF1=1AB1仍然成立,理由详见解析;(3)
,理由见解析23、C24、(1)①详见解析;②详见解析;(1)当BE≠DF时,(BE+DF)1+EF1=1AB1仍然成立,理由详见解析;(3)![]()
相关试卷
这是一份2023-2024学年北京市延庆区八上数学期末质量检测试题含答案,共7页。试卷主要包含了考生必须保证答题卡的整洁,如图,在中,高相交于点,若,则,已知,则的值为,下列各式中,正确的是,下面计算正确的是等内容,欢迎下载使用。
这是一份2023-2024学年北京市延庆县八上数学期末达标测试试题含答案,共7页。试卷主要包含了考生必须保证答题卡的整洁,若,则的值是等内容,欢迎下载使用。
这是一份2022-2023学年北京市延庆区七年级(下)期末数学试卷(含答案解析),共15页。试卷主要包含了3×10−4B, 下列运算正确的是, 计算等内容,欢迎下载使用。









