

内蒙古巴彦淖尔市临河区第二中学2022-2023学年七年级数学第二学期期末质量跟踪监视模拟试题含答案
展开内蒙古巴彦淖尔市临河区第二中学2022-2023学年七年级数学第二学期期末质量跟踪监视模拟试题
(时间:120分钟 分数:120分)
学校_______ 年级_______ 姓名_______
注意事项:
1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其它答案标号。回答非选择题时,将答案写在答题卡上,写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
一、选择题(每小题3分,共30分)
1.已知函数![]() ,不在该函数图象上的点是( )
,不在该函数图象上的点是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
2.下列计算结果,正确的是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
3.若分式![]() 的值为零,则
的值为零,则![]() 的值是( )
的值是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
4.如图,在矩形ABCD中,AB=8,AD=6,过点D作直线m∥AC,点E、F是直线m上两个动点,在运动过程中EF∥AC且EF=AC,四边形ACFE的面积是( )
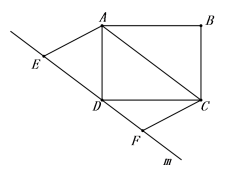
A.48 B.40 C.24 D.30
5.如图,在△ABC中,D,E,F分别是AB,BC,AC边的中点.如果添加一个条件,使四边形ADEF是菱形,则添加的条件为( )
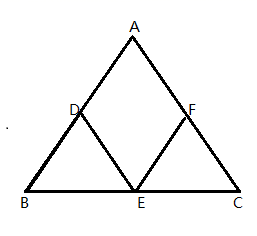
A.AB=AC B.AC=BC C.∠A=90° D.∠A=60°
6.下列计算正确的是( )
A.![]() B.2
B.2![]() C.(
C.(![]() )2=2 D.
)2=2 D.![]() =3
=3
7.甲、乙两个车站相距96千米,快车和慢车同时从甲站开出,1小时后快车在慢车前12千米,快车比慢车早40分钟到达乙站,快车和慢车的速度各是多少?设快车的速度为x千米/时,则下列方程正确的是 ( )
A.![]() -
-![]() =
=![]() B.
B.![]() -
-![]() =40
=40
C.![]() -
-![]() =
=![]() D.
D.![]() -
-![]() =40
=40
8.在函数![]() 的图象上的点是( )
的图象上的点是( )
A.(-2,12) B.(2,- 12) C.(-4,- 6) D.(4,- 6)
9.如图是小明在物理实验课上用量筒和水测量铁块A的体积实验,小明在匀速向上将铁块提起,直至铁块完全露出水面一定高度的过程中,则下图能反映液面高度h与铁块被提起的时间t之间的函数关系的大致图象是( )
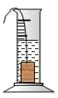
A.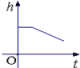 B.
B.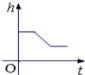 C.
C.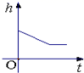 D.
D.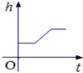
10.下列各组数,可以作为直角三角形的三边长的是( )
A.2,3,4 B.3,4,6 C.4,5,6 D.6,8,10
二、填空题(本大题共有6小题,每小题3分,共18分)
11.面试时,某人的基本知识、表达能力、工作态度的成绩分别是90分、80分、85分,若依次按20%、40%、40%的比例确定成绩,则这个人的面试成绩是_______.
12.已知直线y=kx+3经过点A(2,5)和B(m,-2),则m= ___________.
13.如图所示,将四根木条组成的矩形木框变成▱ABCD的形状,并使其面积变为原来的一半,则这个平行四边形的一个最小的内角的度数是_____.
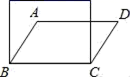
14.如图,有一块菱形纸片ABCD,沿高DE剪下后拼成一个矩形,矩形的长和宽分别是5cm,3cm.EB的长是______.
15.如果![]() 有意义,那么x的取值范围是_____.
有意义,那么x的取值范围是_____.
16.已知关于x的方程(m-1)x2-2x+1=0有两个不相等的实数根,则m的取值范围是_____.
三、解下列各题(本大题共8小题,共72分)
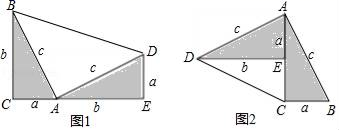
17.(8分)勾股定理神秘而美妙,它的证法多样,其巧妙各有不同,其中的“面积法”给了小聪以灵感,他惊喜的发现,当两个全等的直角三角形如图1或图1摆放时,都可以用“面积法”来证明,请你利用图1或图1证明勾股定理(其中∠DAB=90°)
求证:a1+b1=c1.
18.(8分)已知:如图,在Rt△ABC中,∠C=90°,沿过B点的一条直线BE折叠这个三角形, 使C点与AB边上的一点D重合.
(1)当∠A满足什么条件时,点D恰为AB的中点?写出一个你认为适当的条件,并利用此条件证明D为AB的中点;
(2)在(1)的条件下,若DE=1,求△ABC的面积.
19.(8分)如图,在平行四边形ABCD中,E,F分别是AB,CD的中点,DE,BF与对角线AC分别交于点M,N,连接MF,NE.

(1)求证:DE∥BF
(2)判断四边形MENF是何特殊的四边形?并对结论给予证明;
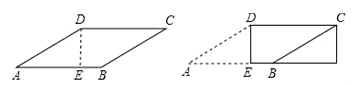
20.(8分)在矩形ABCD中,E是AD延长线上一点,F、G分别为EC、AD的中点,连接BG、CG、BE、FG.
(1)如图1,① 求证:BG=CG;
② 求证:BE=2FG;
(2)如图2,若ED=CD,过点C作CH⊥BE于点H,若BC=4,∠EBC=30°,则EH的长为______________.
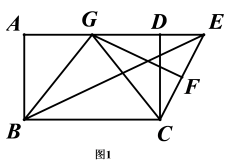
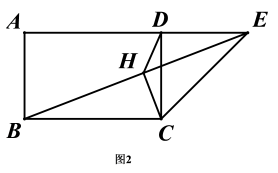
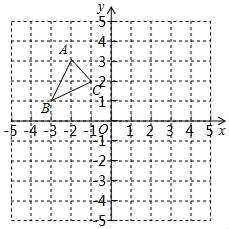
21.(8分)如图,在平面直角坐标系中,已知点A(﹣1,3),B(﹣3,1),C(﹣1,1).且△A1B1C1与△ABC关于原点O成中心对称.
(1)画出△A1B1C1,并写出A1的坐标;
(1)P(a,b)是△ABC的边AC上一点,△ABC经平移后点P的对应点P′(a+3,b+1),请画出平移后的△A1B1C1.
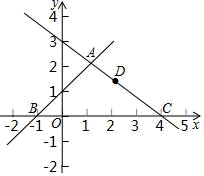
22.(10分)如图,在平面直角坐标系可中,直线y=x+1与y=﹣![]() x+3交于点A,分别交x轴于点B和点C,点D是直线AC上的一个动点.
x+3交于点A,分别交x轴于点B和点C,点D是直线AC上的一个动点.
(1)求点A,B,C的坐标;
(2)在直线AB上是否存在点E使得四边形EODA为平行四边形?存在的话直接写出![]() 的值,不存在请说明理由;
的值,不存在请说明理由;
(3)当△CBD为等腰三角形时直接写出D坐标.
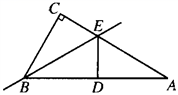
23.(10分)如图,![]() 中,
中,![]() ,
,![]() 是
是![]() 上一点,
上一点,![]() 于点
于点![]() ,
,![]() 是
是![]() 的中点,
的中点,![]() 于点
于点![]() ,与
,与![]() 交于点
交于点![]() ,若
,若![]() ,
,![]() 平分
平分![]() ,连结
,连结![]() ,
,![]() .
.
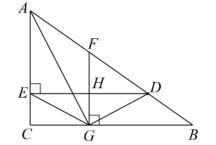
(1)求证:![]() ;
;
(2)求证:![]() .
.
(3)若![]() ,判定四边形
,判定四边形![]() 是否为菱形,并说明理由.
是否为菱形,并说明理由.
24.(12分)9月28日,我国神舟七号载人飞船顺利返回地面,下面是“神舟”七号飞船返回舱返回过程中的相关记录:从返回舱制动点火至减速伞打开期间,返回舱距离地面的高度与时间呈二次函数关系,减速伞打开后,返回舱距离地面的高度与时间呈一次函数关系,高度和时间的对应关系如下表:
时间 | 4:45 | 5:12 | 5:15 | 5:18 | 5:24 | 5:26 | 5:28 |
返回舱距离地面的高度 | 350km | 134km | 80km | 20km | 8km | 4km | 0km |
降落状态 | 返回舱制动点火 | 返回舱高速进入黑障区 | 引导伞引出减速伞 | 减速伞打开 | 返回舱抛掉放热大底 | 着陆系统正式启动 | 返回舱成功降落地面 |
- 设减速伞打开后x分钟,返回舱距离地面的高度为hkm,求h与x的函数关系式。
- 在返回舱在距离地面5km时,要求宇航员打开电磁信号灯以便地面人员搜寻,判断宇航员应在何时开启信号灯?
参考答案
一、选择题(每小题3分,共30分)
1、B
2、C
3、B
4、A
5、A
6、C
7、C
8、C
9、B
10、D
二、填空题(本大题共有6小题,每小题3分,共18分)
11、84分
12、-1
13、30°
14、1cm
15、x>1
16、m<2且m≠1.
三、解下列各题(本大题共8小题,共72分)
17、见解析.
18、(1)∠A=30°;(1)![]() .
.
19、(1)见解析;(2)平行四边形,证明见解析
20、 (1)①见解析,②见解析;(2) ![]()
21、(1)作图见解析;(1)作图见解析.
22、 (1)A(![]() ,
,![]() ),B(﹣1,0),C(4,0);(2)存在,
),B(﹣1,0),C(4,0);(2)存在,![]() =
=![]() ;(3)点D的坐标为(﹣
;(3)点D的坐标为(﹣![]() ,
,![]() )或(8,﹣3)或(0,3)或(
)或(8,﹣3)或(0,3)或(![]() ,
,![]() ).
).
23、(1)见解析;(2)证明见解析;(3)四边形AEGF是菱形,证明见解析.
24、(1)h=-2x+20 (2)5时25分30秒(或减速伞打开后7.5秒)
贵州罗甸民族中学2022-2023学年数学七年级第二学期期末质量跟踪监视模拟试题含答案: 这是一份贵州罗甸民族中学2022-2023学年数学七年级第二学期期末质量跟踪监视模拟试题含答案,共7页。试卷主要包含了考生要认真填写考场号和座位序号,计算+的值等于等内容,欢迎下载使用。
天津市滨湖中学2022-2023学年七年级数学第二学期期末质量跟踪监视模拟试题含答案: 这是一份天津市滨湖中学2022-2023学年七年级数学第二学期期末质量跟踪监视模拟试题含答案,共6页。试卷主要包含了不等式的解在数轴上表示正确的是等内容,欢迎下载使用。
2022-2023学年重庆市巫溪中学数学七年级第二学期期末质量跟踪监视模拟试题含答案: 这是一份2022-2023学年重庆市巫溪中学数学七年级第二学期期末质量跟踪监视模拟试题含答案,共7页。












