


北京市石景山区景山学校2022-2023学年数学七下期末质量检测模拟试题含答案
展开北京市石景山区景山学校2022-2023学年数学七下期末质量检测模拟试题
(时间:120分钟 分数:120分)
学校_______ 年级_______ 姓名_______
考生请注意:
1.答题前请将考场、试室号、座位号、考生号、姓名写在试卷密封线内,不得在试卷上作任何标记。
2.第一部分选择题每小题选出答案后,需将答案写在试卷指定的括号内,第二部分非选择题答案写在试卷题目指定的位置上。
3.考生必须保证答题卡的整洁。考试结束后,请将本试卷和答题卡一并交回。
一、选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.下列二次根式是最简二次根式的是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
2.已知直角三角形的两直角边长分别为3和4,则斜边上的高为( )
A.5 B.3 C.![]() D.
D.![]()
3.下列图形,是中心对称图形的是( )
A.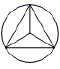 B.
B.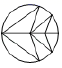 C.
C.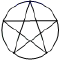 D.
D.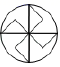
4.等腰三角形的周长为20,设底边长为![]() ,腰长为
,腰长为![]() ,则
,则![]() 关于
关于![]() 的函数解析式为(
的函数解析式为(![]() 为自变量)( )
为自变量)( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
5.反比例函数![]() 经过点(1,
经过点(1,![]() ),则
),则![]() 的值为( )
的值为( )
A.3 B.![]() C.
C.![]() D.
D.![]()
6.古希腊时期,人们认为最美人体的头顶至肚脐的长度与肚脐至足底的长度之比是黄金分割比(黄金分割比0.618)著名的“断臂维纳斯”便是如此.此外最美人体的头顶至咽喉的长度与咽喉至肚脐的长度之比也是黄金分割比.若某人满足上述两个黄金分割比例,且腿长为103cm,头顶至脖子下端的长度为25cm,则其身高可能是( )
A.165cm B.170cm C.175cm D.180cm
7.学校把学生学科的期中、期末两次成绩分别按40%,60%的比例计入学期学科总成绩.小明期中数学成绩是85分,期末数学总成绩是90分,那么他的学期数学成绩( )
A.85分 B.1.5分 C.88分 D.90分
8.如图,矩形![]() 中,
中,![]() ,
,![]() ,
,![]() 、
、![]() 分别是边
分别是边![]() 、
、![]() 上的点,
上的点,![]() 且
且![]() 与
与![]() 之间的距离为4,则
之间的距离为4,则![]() 的长为( )
的长为( )
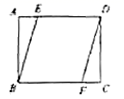
A.3 B.![]() C.
C.![]() D.
D.![]()
9.一艘轮船在静水中的最大航速为![]() ,它以最大航速沿河顺流航行
,它以最大航速沿河顺流航行![]() 所用时间,和它以最大航速沿河逆流航行
所用时间,和它以最大航速沿河逆流航行![]() 所用时间相等,设河水的流速为
所用时间相等,设河水的流速为![]() ,则可列方程为( )
,则可列方程为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
10.如图,边长为2的菱形ABCD中,∠A=60º,点M是边AB上一点,点N是边BC上一点,且∠ADM=15º,∠MDN=90º,则点B到DN的距离为( )
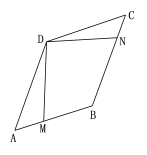
A.![]() B.
B.![]() C.
C.![]() D.2
D.2
11.如图,在△ABC中,点D,E分别在边AB,AC上,DE∥BC,已知AE=6,![]() ,则EC的长是( )
,则EC的长是( )
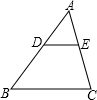
A.4.5 B.8 C.10.5 D.14
12.下列选项中的图形,不属于中心对称图形的是( )
A.
![]() B.
B.
![]() C.
C.
![]() D.
D.
二、填空题(每题4分,满分20分,将答案填在答题纸上)
13.如果反比例函数![]() 的图象在当
的图象在当![]() 的范围内,
的范围内,![]() 随着
随着![]() 的增大而增大,那么
的增大而增大,那么![]() 的取值范围是________.
的取值范围是________.
14.如图,四边形![]() 是正方形,点
是正方形,点![]() 在
在![]() 上,
上,![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 后能够与
后能够与![]() 重合,若
重合,若![]() ,
,![]() ,试求
,试求![]() 的长是__________.
的长是__________.
15.如图,□ABCD与□DCFE的周长相等,且∠BAD=60°,∠F=110°,则∠DAE的度数为_______°.
16.方程x2=x的解是_____.
17.将一次函数y=5x﹣1的图象向上平移3个单位,所得直线不经过第_____象限.
三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)
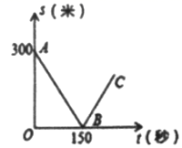
18.(5分)甲、乙两名自行车爱好者准备在段长为3500米的笔直公路上进行比赛,比赛开始时乙在起点,甲在乙的前面.他们同时出发,匀速前进,已知甲的速度为12米/秒,设甲、乙两人之间的距离为s(米),比赛时间为t(秒),图中的折线表示从两人出发至其中一人先到达终点的过程中s(米)与t(秒)的函数关系根据图中信息,回答下列问题:
(1)乙的速度为多少米/秒;
(2)当乙追上甲时,求乙距起点多少米;
(3)求线段BC所在直线的函数关系式.
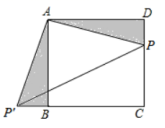
19.(5分)如图,在矩形ABCD中,![]() ,
,![]() .将矩形ABCD沿过点C的直线折叠,使点B落在对角线AC上的点E处,折痕交AB于点F.
.将矩形ABCD沿过点C的直线折叠,使点B落在对角线AC上的点E处,折痕交AB于点F.
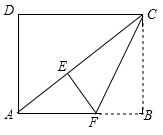
(1)求线段AC的长.
(2)求线段EF的长.
(3)点G在线段CF上,在边CD上存在点H,使以E、F、G、H为顶点的四边形是平行四边形,请画出![]() ,并直接写出线段DH的长.
,并直接写出线段DH的长.
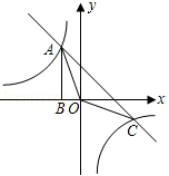
20.(8分)如图,Rt△ABO的顶点A是双曲线y1=![]() 与直线y2=-x-(k+1)在第二象限的交点.AB⊥x轴于B,且S△ABO=
与直线y2=-x-(k+1)在第二象限的交点.AB⊥x轴于B,且S△ABO=![]() .
.
(1)求这两个函数的解析式;
(2)求△AOC的面积.
(3)直接写出使y1>y2成立的x的取值范围
21.(10分)已知直线l为x+y=8,点P(x,y)在l上且x>0,y>0,点A的坐标为(6,0).
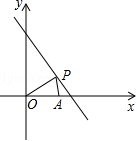
(1)设△OPA的面积为S,求S与x的函数关系式,并直接写出x的取值范围;
(2)当S=9时,求点P的坐标;
(3)在直线l上有一点M,使OM+MA的和最小,求点M的坐标.
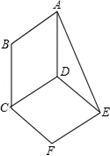
22.(10分)如图:在▱ABCD中,E、F分别为对角线BD上的点,且BE=DF,判断四边形AECF的形状,并说明理由.
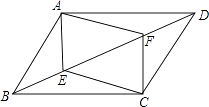
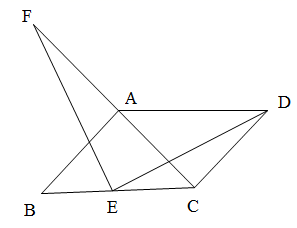
23.(12分)如图,在平行四边形![]() 中,连接
中,连接![]() ,
,![]() ,且
,且![]() ,
,![]() 是
是![]() 的中点,
的中点,![]() 是
是![]() 延长线上一点,且
延长线上一点,且![]() .求证:
.求证:![]() .
.
参考答案
一、选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1、C
2、D
3、D
4、C
5、B
6、B
7、C
8、D
9、C
10、B
11、B
12、B
二、填空题(每题4分,满分20分,将答案填在答题纸上)
13、![]()
14、![]() .
.
15、![]()
16、x1=0,x2=1
17、四
三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)
18、 (1)14;(2)乙距起点2100米;(3)BC所在直线的函数关系式为s=2t-300.
19、(1)![]() ;(2)
;(2)![]() ;(3)见解析,
;(3)见解析,![]() .
.
20、(1)y=﹣![]() ,y=﹣x+2;(2)3;(1)-1<x<0或x>1
,y=﹣x+2;(2)3;(1)-1<x<0或x>1
21、(1)、y=24﹣3x(0<x<8);(2)、P(5,3);(3)、(6.4,1.6).
22、证明见解析
23、证明步骤见解析
2023-2024学年北京市石景山区景山学校八上数学期末达标检测模拟试题含答案: 这是一份2023-2024学年北京市石景山区景山学校八上数学期末达标检测模拟试题含答案,共7页。试卷主要包含了下列各组条件中能判定的是等内容,欢迎下载使用。
北京市石景山区景山学校2023-2024学年数学八上期末学业质量监测模拟试题含答案: 这是一份北京市石景山区景山学校2023-2024学年数学八上期末学业质量监测模拟试题含答案,共6页。试卷主要包含了下列各点中,位于第四象限的点是,下列说法正确的是,如图,,,,则的度数是,下列运算正确的是等内容,欢迎下载使用。
北京市石景山区2022-2023学年数学七下期末达标测试试题含答案: 这是一份北京市石景山区2022-2023学年数学七下期末达标测试试题含答案,共7页。试卷主要包含了考生必须保证答题卡的整洁,函数y=中自变量x的取值范围是,若分式有意义,则的取值范围是,下列计算或化简正确的是等内容,欢迎下载使用。












