


北京市西城区2022-2023学年七下数学期末统考模拟试题含答案
展开
这是一份北京市西城区2022-2023学年七下数学期末统考模拟试题含答案,共7页。试卷主要包含了一组数,分式的计算结果是,若分式的值为0,则,在中,若是的正比例函数,则值为等内容,欢迎下载使用。
北京市西城区2022-2023学年七下数学期末统考模拟试题(时间:120分钟 分数:120分) 学校_______ 年级_______ 姓名_______ 考生须知:1.全卷分选择题和非选择题两部分,全部在答题纸上作答。选择题必须用2B铅笔填涂;非选择题的答案必须用黑色字迹的钢笔或答字笔写在“答题纸”相应位置上。2.请用黑色字迹的钢笔或答字笔在“答题纸”上先填写姓名和准考证号。3.保持卡面清洁,不要折叠,不要弄破、弄皱,在草稿纸、试题卷上答题无效。 一、选择题(每小题3分,共30分)1.某交警在一个路口统计某时间段来往车辆的车速情况如下表,则上述车速的中位数和众数分别是( )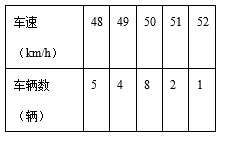 A.50,8 B.50,50 C.49,50 D.49,82.如图,四边形ABCD中,对角线相交于点O,E、F、G、H分别是AD、BD、BC、AC的中点,要使四边形EFGH是矩形,则四边形ABCD需要满足的条件是
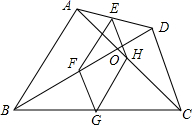
A.50,8 B.50,50 C.49,50 D.49,82.如图,四边形ABCD中,对角线相交于点O,E、F、G、H分别是AD、BD、BC、AC的中点,要使四边形EFGH是矩形,则四边形ABCD需要满足的条件是![]()
![]()
 A.
A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 3.在实数范围内,
3.在实数范围内,![]() 有意义,则x的取值范围是( )A.x≥0 B.x≤0 C.x>0 D.x<04.已知正比例函数y=kx,且y随x的增大而减少,则直线y=2x+k的图象是( )A.
有意义,则x的取值范围是( )A.x≥0 B.x≤0 C.x>0 D.x<04.已知正比例函数y=kx,且y随x的增大而减少,则直线y=2x+k的图象是( )A.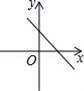 B.
B.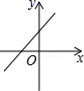 C.
C.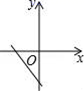 D.
D.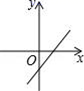 5.如图,在正方形
5.如图,在正方形![]() 中,点
中,点![]() ,
,![]() 分别在
分别在![]() ,
,![]() 上,
上,![]() ,
,![]() 与
与![]() 相交于点
相交于点![]() .下列结论:①
.下列结论:①![]() 垂直平分
垂直平分![]() ;②
;②![]() ;③当
;③当![]() 时,
时,![]() 为等边三角形;④当
为等边三角形;④当![]() 时,
时,![]() .其中正确的结论是( )
.其中正确的结论是( )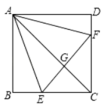 A.①③ B.②④ C.①③④ D.②③④6.如图,在Rt△ABC中,AB=AC,D,E是斜边上BC上两点,且∠DAE=45°,将△ADC绕点A顺时针旋转90°后,得到△AFB,连接EF,下列结论:①BF⊥BC;②△AED≌△AEF;③BE+DC=DE;④BE
A.①③ B.②④ C.①③④ D.②③④6.如图,在Rt△ABC中,AB=AC,D,E是斜边上BC上两点,且∠DAE=45°,将△ADC绕点A顺时针旋转90°后,得到△AFB,连接EF,下列结论:①BF⊥BC;②△AED≌△AEF;③BE+DC=DE;④BE![]() +DC
+DC![]() =DE
=DE![]() 其中正确的个数是( )
其中正确的个数是( )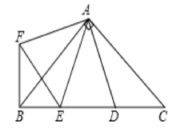 A.1 B.2 C.0 D.37.一组数:3,5,4,2,3的中位数是( )A.2 B.3 C.3.5 D.48.分式
A.1 B.2 C.0 D.37.一组数:3,5,4,2,3的中位数是( )A.2 B.3 C.3.5 D.48.分式![]() 的计算结果是( )A.
的计算结果是( )A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 9.若分式
9.若分式![]() 的值为0,则( )A.
的值为0,则( )A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 10.在
10.在![]() 中,若
中,若![]() 是
是![]() 的正比例函数,则
的正比例函数,则![]() 值为
值为![]()
![]() A.1 B.
A.1 B.![]() C.
C.![]() D.无法确定二、填空题(本大题共有6小题,每小题3分,共18分)11.方程
D.无法确定二、填空题(本大题共有6小题,每小题3分,共18分)11.方程![]() 的解为_________.12.如图,△ABC是边长为6的等边三角形,D是AB中点,E是边BC上一动点,连结DE,将DE绕点D逆时针旋转60°得DF,连接CF,若CF=
的解为_________.12.如图,△ABC是边长为6的等边三角形,D是AB中点,E是边BC上一动点,连结DE,将DE绕点D逆时针旋转60°得DF,连接CF,若CF=![]() ,则BE=_________。
,则BE=_________。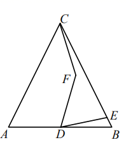 13.一次函数y=kx+b的图象如图所示,则不等式kx+b<0的解集为__________.
13.一次函数y=kx+b的图象如图所示,则不等式kx+b<0的解集为__________.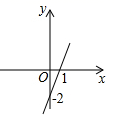 14.若点
14.若点![]() 在
在![]() 轴上,则点
轴上,则点![]() 的坐标为__________.15.如图,四边形ABCD是梯形,AD∥BC,AC=BD,且AC⊥BD,如果梯形ABCD的中位线长是5,那么这个梯形的高AH=___.
的坐标为__________.15.如图,四边形ABCD是梯形,AD∥BC,AC=BD,且AC⊥BD,如果梯形ABCD的中位线长是5,那么这个梯形的高AH=___.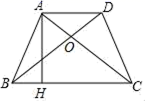 16.在平面直角坐标系内,直线l⊥y轴于点C(C在y轴的正半轴上),与直线y=
16.在平面直角坐标系内,直线l⊥y轴于点C(C在y轴的正半轴上),与直线y=![]() 相交于点A,和双曲线y=
相交于点A,和双曲线y=![]() 交于点B,且AB=6,则点B的坐标是______.三、解下列各题(本大题共8小题,共72分)17.(8分)综合与实践(问题情境)在综合与实践课上,同学们以“矩形的折叠”为主题展开数学活动,如图1,在矩形纸片ABCD中,AB=4,BC=5,点E,F分别为边AB,AD上的点,且DF=3。(操作发现)(1)沿CE折叠纸片,B点恰好与F点重合,求AE的长;(2)如图2,延长EF交CD的延长线于点M,请判断△CEM的形状,并说明理由。(深入思考) (3)把图2置于平面直角坐标系中,如图3,使D点与原点O重合,C点在x轴的负半轴上,将△CEM沿CE翻折,使点M落在点M′处.连接CM′,求点M′的坐标.
交于点B,且AB=6,则点B的坐标是______.三、解下列各题(本大题共8小题,共72分)17.(8分)综合与实践(问题情境)在综合与实践课上,同学们以“矩形的折叠”为主题展开数学活动,如图1,在矩形纸片ABCD中,AB=4,BC=5,点E,F分别为边AB,AD上的点,且DF=3。(操作发现)(1)沿CE折叠纸片,B点恰好与F点重合,求AE的长;(2)如图2,延长EF交CD的延长线于点M,请判断△CEM的形状,并说明理由。(深入思考) (3)把图2置于平面直角坐标系中,如图3,使D点与原点O重合,C点在x轴的负半轴上,将△CEM沿CE翻折,使点M落在点M′处.连接CM′,求点M′的坐标.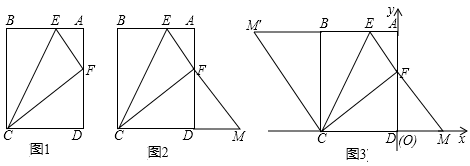 18.(8分)如图,在平行四边形ABCD中,
18.(8分)如图,在平行四边形ABCD中,![]() ,延长DA于点E,使得
,延长DA于点E,使得![]() ,连接BE.
,连接BE.![]() 求证:四边形AEBC是矩形;
求证:四边形AEBC是矩形;![]() 过点E作AB的垂线分别交AB,AC于点F,G,连接CE交AB于点O,连接OG,若
过点E作AB的垂线分别交AB,AC于点F,G,连接CE交AB于点O,连接OG,若![]() ,
,![]() ,求
,求![]() 的面积.
的面积.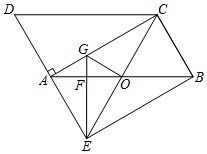 19.(8分)如图,□ABCD中,BD是它的一条对角线,过A、C两点作AE⊥BD,CF⊥BD,垂足分别为E、F,延长AE、CF分别交CD、AB于M、N.
19.(8分)如图,□ABCD中,BD是它的一条对角线,过A、C两点作AE⊥BD,CF⊥BD,垂足分别为E、F,延长AE、CF分别交CD、AB于M、N.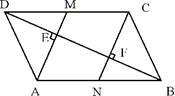 (1)求证:四边形CMAN是平行四边形.(2)已知DE=4,FN=3,求BN的长. 20.(8分)甲乙两人参加某项体育训练,近期五次测试成绩得分情况如图所示:(1)分别求出两人得分的平均数;(2)谁的方差较大?(3)根据图表和(1)的计算,请你对甲、乙两人的训练成绩作出评价.
(1)求证:四边形CMAN是平行四边形.(2)已知DE=4,FN=3,求BN的长. 20.(8分)甲乙两人参加某项体育训练,近期五次测试成绩得分情况如图所示:(1)分别求出两人得分的平均数;(2)谁的方差较大?(3)根据图表和(1)的计算,请你对甲、乙两人的训练成绩作出评价.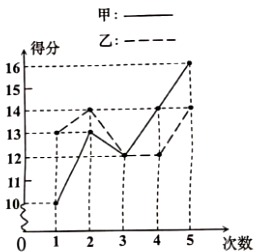 21.(8分)已知一次函数y=(3-k)x-2k2+18.(1)当k为何值时,它的图象经过原点?(2)当k为何值时,它的图象经过点(0,-2)?(3)当k为何值时,它的图象平行于直线y=-x?(4)当k为何值时,y随x增大而减小? 22.(10分)某市射击队甲、乙两名队员在相同的条件下各射耙10次,每次射耙的成绩情况如图所示:(1)请将下表补充完整:(参考公式:方差S2=
21.(8分)已知一次函数y=(3-k)x-2k2+18.(1)当k为何值时,它的图象经过原点?(2)当k为何值时,它的图象经过点(0,-2)?(3)当k为何值时,它的图象平行于直线y=-x?(4)当k为何值时,y随x增大而减小? 22.(10分)某市射击队甲、乙两名队员在相同的条件下各射耙10次,每次射耙的成绩情况如图所示:(1)请将下表补充完整:(参考公式:方差S2=![]() [(x1﹣
[(x1﹣![]() )2+(x2﹣
)2+(x2﹣![]() )2+…+(xn﹣
)2+…+(xn﹣![]() )2]) 平均数方差中位数甲7 7乙 5.4 (2)请从下列三个不同的角度对这次测试结果进行分析:①从平均数和方差相结合看, 的成绩好些;②从平均数和中位数相结合看, 的成绩好些;③若其他队选手最好成绩在9环左右,现要选一人参赛,你认为选谁参加,并说明理由.
)2]) 平均数方差中位数甲7 7乙 5.4 (2)请从下列三个不同的角度对这次测试结果进行分析:①从平均数和方差相结合看, 的成绩好些;②从平均数和中位数相结合看, 的成绩好些;③若其他队选手最好成绩在9环左右,现要选一人参赛,你认为选谁参加,并说明理由.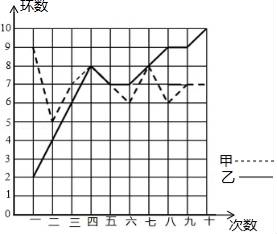 23.(10分)如图,在平行四边形OABC中,已知点A、C两点的坐标为A (
23.(10分)如图,在平行四边形OABC中,已知点A、C两点的坐标为A (![]() ,
,![]() ),C (2
),C (2![]() ,0).(1)求点B的坐标.(2)将平行四边形OABC向左平移
,0).(1)求点B的坐标.(2)将平行四边形OABC向左平移![]() 个单位长度,求所得四边形A′B′C′O′四个顶点的坐标.(3)求平行四边形OABC的面积.
个单位长度,求所得四边形A′B′C′O′四个顶点的坐标.(3)求平行四边形OABC的面积.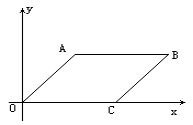 24.(12分)如图,在△ABC中,AD平分∠BAC,AB+BD=AC,∠BAC=75°,则∠C的度数为____.
24.(12分)如图,在△ABC中,AD平分∠BAC,AB+BD=AC,∠BAC=75°,则∠C的度数为____.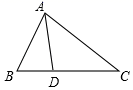 参考答案 一、选择题(每小题3分,共30分)1、B2、B3、A4、D5、A6、D7、B8、C9、C10、A 二、填空题(本大题共有6小题,每小题3分,共18分)11、
参考答案 一、选择题(每小题3分,共30分)1、B2、B3、A4、D5、A6、D7、B8、C9、C10、A 二、填空题(本大题共有6小题,每小题3分,共18分)11、![]() 12、1或213、x<114、
12、1或213、x<114、![]() 15、1.16、(3+
15、1.16、(3+![]() ,
,![]() )或(-3+
)或(-3+![]() ,
,![]() ) 三、解下列各题(本大题共8小题,共72分)17、 (1) AE的长为
) 三、解下列各题(本大题共8小题,共72分)17、 (1) AE的长为![]() ;(2)ΔCEM是等腰三角形,理由见解析; (3)M′(-
;(2)ΔCEM是等腰三角形,理由见解析; (3)M′(-![]() ,5).18、(1)见解析;(2)
,5).18、(1)见解析;(2)![]() .19、(1)详见解析;(2)1.20、(1)13,13;(2)4,0.8;甲的方差大;(3)从平均数来看甲乙训练成绩一样,从图中可以看中,乙比较稳定,甲波动大.21、 (1)见解析;(2) k=±
.19、(1)详见解析;(2)1.20、(1)13,13;(2)4,0.8;甲的方差大;(3)从平均数来看甲乙训练成绩一样,从图中可以看中,乙比较稳定,甲波动大.21、 (1)见解析;(2) k=±![]() ;(1) k=4;(4) k>1.22、(1)1.2,7,7.5;(2)甲,乙,乙,理由见解析.23、 (1)点B坐标是(3
;(1) k=4;(4) k>1.22、(1)1.2,7,7.5;(2)甲,乙,乙,理由见解析.23、 (1)点B坐标是(3![]() ,
,![]() );(2) A′(O,
);(2) A′(O, ![]() )、B′(2
)、B′(2![]() ,
,![]() )、C′(
)、C′(![]() ,0),O′(-
,0),O′(-![]() ,0);(3) 6.24、35°.
,0);(3) 6.24、35°.
相关试卷
这是一份北京市西城区第十五中学2022-2023学年七下数学期末统考模拟试题含答案,共6页。试卷主要包含了答题时请按要求用笔,下列各式中,运算正确的是等内容,欢迎下载使用。
这是一份北京市海淀区名校2022-2023学年数学七下期末统考模拟试题含答案,共7页。试卷主要包含了考生要认真填写考场号和座位序号,下列判断中,错误的是,函数与等内容,欢迎下载使用。
这是一份北京市三十一中学2022-2023学年数学七下期末统考模拟试题含答案,共8页。试卷主要包含了下列说法中,正确的是等内容,欢迎下载使用。









