


北京市燕山地区2022-2023学年七下数学期末综合测试试题含答案
展开这是一份北京市燕山地区2022-2023学年七下数学期末综合测试试题含答案,共8页。
北京市燕山地区2022-2023学年七下数学期末综合测试试题
(时间:120分钟 分数:120分)
学校_______ 年级_______ 姓名_______
请考生注意:
1.请用2B铅笔将选择题答案涂填在答题纸相应位置上,请用0.5毫米及以上黑色字迹的钢笔或签字笔将主观题的答案写在答题纸相应的答题区内。写在试题卷、草稿纸上均无效。
2.答题前,认真阅读答题纸上的《注意事项》,按规定答题。
一、选择题(每小题3分,共30分)
1.下列等式从左边到右边的变形,是因式分解的是( )
A.(3﹣a)(3+a)=9﹣a2 B.x2﹣y2+1=(x+y)(x﹣y)+1
C.a2+1=a(a+![]() ) D.m2﹣2mn+n2=(m﹣n)2
) D.m2﹣2mn+n2=(m﹣n)2
2.如果a为任意实数, 下列各式中一定有意义的是( )
A.![]() B.
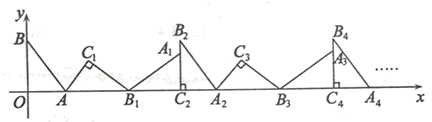
B.![]() C.
C.![]() D.
D.![]()
3.如图,已知一次函数![]() 的图象与x轴,y轴分别交于点(2,0),点(0,3).有下列结论:①关于x的方程
的图象与x轴,y轴分别交于点(2,0),点(0,3).有下列结论:①关于x的方程![]() 的解为
的解为![]() ;②关于x的方程
;②关于x的方程![]() 的解为
的解为![]() ;③当
;③当![]() 时,
时,![]() ;④当
;④当![]() 时,
时,![]() .其中正确的是( )
.其中正确的是( )
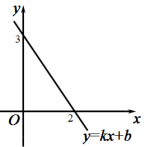
A.①②③ B.①③④ C.②③④ D.①②④
4.若代数式![]() 在实数范围内有意义,则
在实数范围内有意义,则![]() 的取值范围是
的取值范围是![]()
![]()
A.x<1 B.x≤1 C.x>1 D.x≥1
5.下列各点中,在反比例函数y=![]() 图象上的是( )
图象上的是( )
A.(2,3) B.(﹣1,6) C.(2,﹣3) D.(﹣12,﹣2)
6.将五个边长都为 2![]() 的正方形按如图所示摆放,点
的正方形按如图所示摆放,点 ![]() 分别是四个正方形的中心,则图中四块阴影面积的和为( )
分别是四个正方形的中心,则图中四块阴影面积的和为( )

A.2![]() B.4
B.4![]() C.6
C.6![]() D.8
D.8![]()
7.如图, 四边形![]() 是平行四边形,对角线
是平行四边形,对角线![]() 、
、![]() 交于点
交于点![]() ,
,![]() 是
是![]() 的中点,以下说法错误的是( )
的中点,以下说法错误的是( )
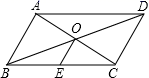
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
8.汽车开始行使时,油箱内有油![]() 升,如果每小时耗油
升,如果每小时耗油![]() 升,则油箱内剩余油量
升,则油箱内剩余油量![]() (升)与行驶时间
(升)与行驶时间![]() (时的关系式为( )
(时的关系式为( )
A.![]() B.
B.![]() C.
C.![]() D.以上答案都不对
D.以上答案都不对
9.如图,正方形ABCD中,AB=6,点E在边CD上,且CD=1DE.将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG、CF.下列结论:①△ABG≌△AFG;②BG=GC;③AG∥CF;④S△FGC=1.其中正确结论的个数是( )
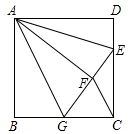
A.1 B.2 C.1 D.4
10.函数y=![]() 中,自变量x的取值范围在数轴上表示正确的是( )
中,自变量x的取值范围在数轴上表示正确的是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
二、填空题(本大题共有6小题,每小题3分,共18分)
11.在式子![]() 中,x的取值范围是__________________.
中,x的取值范围是__________________.
12.阅读下面材料:
小明想探究函数![]() 的性质,他借助计算器求出了y与x的几组对应值,并在平面直角坐标系中画出了函数图象:
的性质,他借助计算器求出了y与x的几组对应值,并在平面直角坐标系中画出了函数图象:
x | … | -3 | -2 | -1 | 1 | 2 | 3 | … |
y | … | 2.83 | 1.73 | 0 | 0 | 1.73 | 2.83 | … |
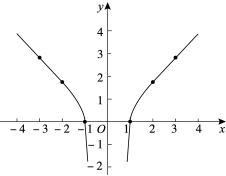
小聪看了一眼就说:“你画的图象肯定是错误的.”
请回答:小聪判断的理由是 .请写出函数![]() 的一条性质: .
的一条性质: .
13.一组数据2,3,x,5,7的平均数是4,则这组数据的众数是 .
14.用换元法解方程![]() 时,如果设
时,如果设![]() ,那么所得到的关于
,那么所得到的关于![]() 的整式方程为_____________
的整式方程为_____________
15.如图,在平面直角坐标系中,将△ABO绕点A顺时针旋转到![]() 的位置,点B、O分别落在点
的位置,点B、O分别落在点![]() 、
、![]() 处,点
处,点![]() 在x轴上,再将
在x轴上,再将![]() 绕点
绕点![]() 顺时针旋转到
顺时针旋转到![]() 的位置,点
的位置,点![]() 在x轴上,将
在x轴上,将![]() 绕点
绕点![]() 顺时针旋转到
顺时针旋转到![]() 的位置,点
的位置,点![]() 在x轴上,依次进行下去…若点
在x轴上,依次进行下去…若点![]() ,
,![]() ,则点
,则点![]() 的坐标为________.
的坐标为________.
16.一支蜡烛长10cm,点燃时每分钟燃烧0.2cm,则点燃后蜡烛长度![]() (cm)随点燃时间
(cm)随点燃时间![]() (min)而变化的函数关系式为_____________________,自变量
(min)而变化的函数关系式为_____________________,自变量![]() 的取值范围是________________.
的取值范围是________________.
三、解下列各题(本大题共8小题,共72分)
17.(8分)在学校组织的知识竞赛活动中,老师将八年级一班和二班全部学生的成绩整理并绘制成如下统计表:
得分(分) 人数(人) 班级 | 50 | 60 | 70 | 80 | 90 | 100 |
一班 | 2 | 5 | 10 | 13 | 14 | 6 |
二班 | 4 | 4 | 16 | 2 | 12 | 12 |
(1)现已知一班和二班的平均分相同,请求出其平均分.
(2)请分别求出这两班的中位数和众数,并进一步分析这两个班级在这次竞赛中成绩的情况.
18.(8分)解下列方程
(1)3x2-9x=0
(2)4x2-3x-1=0
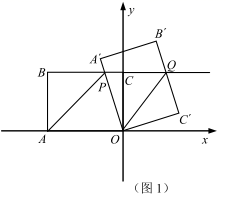
19.(8分)如图1,![]() 为坐标原点,矩形
为坐标原点,矩形![]() 的顶点
的顶点![]() ,
,![]() ,将矩形
,将矩形![]() 绕点
绕点![]() 按顺时针方向旋转一定的角度
按顺时针方向旋转一定的角度![]() 得到矩形
得到矩形![]() ,此时边
,此时边![]() 、直线
、直线![]() 分别与直线
分别与直线![]() 交于点
交于点![]() 、
、![]() .
.
(1)连接![]() ,在旋转过程中,当
,在旋转过程中,当![]() 时,求点
时,求点![]() 坐标.
坐标.
(2)连接![]() ,当
,当![]() 时,若
时,若![]() 为线段
为线段![]() 中点,求
中点,求![]() 的面积.
的面积.
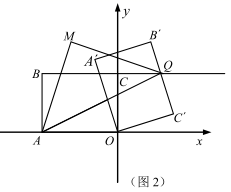
(3)如图2,连接![]() ,以
,以![]() 为斜边向上作等腰直角
为斜边向上作等腰直角![]() ,请直接写出在旋转过程中
,请直接写出在旋转过程中![]() 的最小值.
的最小值.
20.(8分)如图,⊙O为ABC的外接圆,D为OC与AB的交点,E为线段OC延长线上一点,且EACABC.
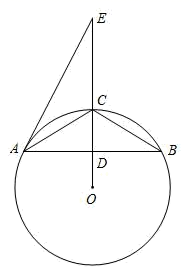
(1)求证:直线AE是⊙O的切线;
(2)若D为AB的中点,CD3,AB8.
①求⊙O的半径;②求ABC的内心I到点O的距离.
21.(8分)某校全体同学参加了某项捐款活动,随机抽查了部分同学捐款的情况,并统计绘制成了如图两幅不完整的条形统计图和扇形统计图,请根据所提供的信息,解答下列问题:
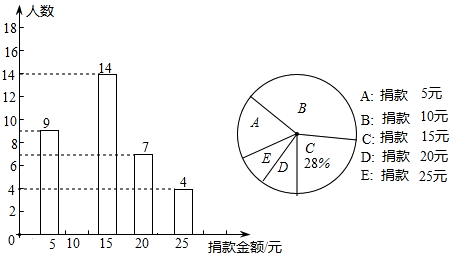
(1)本次共抽查学生 人,并将条形图补充完整:
(2)捐款金额的众数是 元,中位数是 元;
(3)若该校共有2000名学生参加捐款,根据样本平均数估计该校大约可捐款多少元?
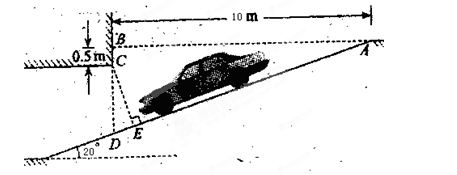
22.(10分)为缓解“停车难”的问题,某单位拟建造地下停车库,建筑设计师提供了该地下停车库的设计示意图,按规定,地下停车库坡道口上方要张贴限高标志,以便告知停车人车辆能否安全驶入,为标明限高,请你根据该图计算CE.(精确到0.1m)
(下列数据提供参考:![]() 20°=0.3420,
20°=0.3420,![]() 20°=0.9397,
20°=0.9397,![]() 20°=0.3640)
20°=0.3640)
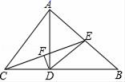
23.(10分)如图,AD是△ABC的高,CE是△ABC的中线.
(1)若AD=12,BD=16,求DE;
(2)已知点F是中线CE的中点,连接DF,若∠AEC=57°,∠DFE=90°,求∠BCE的度数.
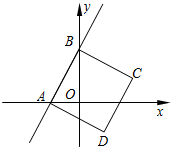
24.(12分)如图,一次函数y=2x+4的图象与x、y轴分别相交于点A、B,四边形ABCD是正方形.
(1)求点A、B、D的坐标;
(2)求直线BD的表达式.
参考答案
一、选择题(每小题3分,共30分)
1、D
2、C
3、A
4、D
5、A
6、B
7、D
8、C
9、C
10、B
二、填空题(本大题共有6小题,每小题3分,共18分)
11、x≥2
12、如:因为函数值不可能为负,所以在x轴下方不会有图象; 当x≤-1时,y随x增大而减小,当x≥1时,y随x增大而增大
13、3
14、![]()
15、(1,2)
16、y=10-0.2x 0≤x≤50
三、解下列各题(本大题共8小题,共72分)
17、 (1)平均分为80分;(2)一班的众数为90分、中位数为80分;二班的众数为70分、中位数为80分;分析见解析.
18、(1)x1=0,x2=3;(2)x1=1,x2=-![]() .
.
19、(1)P(﹣4,6);(2)![]() ;(3)
;(3)![]()
20、(1)见解析;(2)①⊙O的半径![]() ;②ABC的内心I到点O的距离为
;②ABC的内心I到点O的距离为![]() .
.
21、(1)50,见解析;(2)10,12.5;(3)根据样本平均数估计该校大约可捐款26200元.
22、限高应标3.0![]() .
.
23、(1)DE=10;(2)∠BCE=19°.
24、(1)A(﹣2,0),点B(0,1),D(2,﹣2);(2)y=﹣3x+1.
相关试卷
这是一份2023-2024学年北京市房山区燕山地区八上数学期末统考模拟试题含答案,共6页。试卷主要包含了考生必须保证答题卡的整洁,把式子化筒的结果为,下列因式分解结果正确的有等内容,欢迎下载使用。
这是一份2022-2023学年浙江地区数学七下期末综合测试试题含答案,共8页。试卷主要包含了考生要认真填写考场号和座位序号,使有意义的x的取值范围是,正方形有而矩形不一定有的性质是等内容,欢迎下载使用。
这是一份2022-2023学年安徽界首地区七下数学期末综合测试模拟试题含答案,共7页。












