南省郴州市2022-2023学年数学七下期末考试试题含答案

这是一份南省郴州市2022-2023学年数学七下期末考试试题含答案，共7页。试卷主要包含了考生必须保证答题卡的整洁，点P的坐标为，在四边形ABCD中，AC＝BD等内容，欢迎下载使用。
南省郴州市2022-2023学年数学七下期末考试试题（时间：120分钟             分数：120分） 学校_______            年级_______        姓名_______ 考生请注意：1．答题前请将考场、试室号、座位号、考生号、姓名写在试卷密封线内，不得在试卷上作任何标记。2．第一部分选择题每小题选出答案后，需将答案写在试卷指定的括号内，第二部分非选择题答案写在试卷题目指定的位置上。3．考生必须保证答题卡的整洁。考试结束后，请将本试卷和答题卡一并交回。 一、选择题：本大题共12个小题，每小题3分，共36分.在每小题给出的四个选项中，只有一项是符合题目要求的.1．下列命题中，正确的是（　　）A．平行四边形的对角线相等B．矩形的对角线互相垂直C．菱形的对角线互相垂直且平分D．对角线相等的四边形是矩形2．某学校拟建一间矩形活动室，一面靠墙(墙足够长)，中间用一道墙隔开，并在如图所示的三处各留1m宽的门，已知计划中的材料可建墙体(不包括门)总长为27m，建成后的活动室面积为75m2，求矩形活动室的长和宽，若设矩形宽为x，根据题意可列方程为(   )A．x(27﹣3x)＝75 B．x(3x﹣27)＝75C．x(30﹣3x)＝75 D．x(3x﹣30)＝753．下列事件为随机事件的是（    ）A．367人中至少有2人生日相同 B．打开电视，正在播广告C．没有水分，种子发芽 D．如果、都是实数，那么4．如图,Rt△ABC中,∠ACB=90°,若AB=15,则正方形ADEC和正方形BCFG的面积之和为( 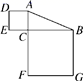   )A．150 B．200 C．225 D．无法计算5．如图，将两块完全相同的矩形纸片ABCD和矩形纸片AEFG按图示方式放置（点A、D、E在同一直线上），连接AC、AF、CF，已知AD＝3，DC＝4，则CF的长是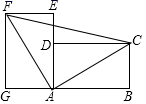（　　）A．5 B．7 C．5 D．106．点P的坐标为（﹣3，2），把点P向右平移2个单位后再向下平移5个单位得到点P1，则点P1的坐标为（　　）A．（﹣1，2） B．（﹣5，﹣3） C．（﹣1，﹣3） D．（﹣1，7）7．下列调查中，适宜采用抽样调查方式的是（   ）A．调查八年级某班学生的视力情况B．调查乘坐飞机的旅客是否携带违禁物品C．调查某品牌LED灯的使用寿命D．学校在给学生订制校服前尺寸大小的调查8．在四边形ABCD中，AC＝BD．顺次连接四边形ABCD四边中点E、F、G、H，则四边形EFGH的形状是（　　）A．矩形 B．菱形 C．正方形 D．不能确定9．一次函数y1=kx+b与y2=x+a的图象如图，则下列结论：①k＜1；②a＞1；③当x＜4时，y1＜y2；④b＜1．其中正确结论的个数是( 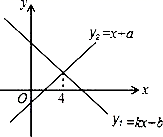  )A．4个 B．3个 C．2个 D．1个10．如图，在△ABC中，∠B＝45°，∠ACB＝60°，AB＝16，AD⊥BC，垂足为D，∠ACB的平分线交AD于点E，则AE的长为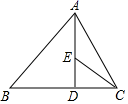（　　）A． B．4 C． D．611．已知菱形的两条对角线的长分别是6和8，则菱形的周长是（    ）A．36 B．30 C．24 D．2012．已知m、n是正整数，若+是整数，则满足条件的有序数对（m，n）为（　　）A．（2，5） B．（8，20） C．（2，5），（8，20） D．以上都不是二、填空题（每题4分，满分20分，将答案填在答题纸上）13．设函数与的图象的交点坐标为，则的值为__________.14．已知直线，则直线关于轴对称的直线函数关系式是__________．15．在数轴上表示实数a的点如图所示，化简＋|a－2|的结果为____________．16．如图,将边长为12的正方形ABCD沿其对角线AC剪开,再把△ABC沿着AD方向平移,得到△A′B′C′,当两个三角形重叠部分的面积为32时,它移动的距离AA′等于________.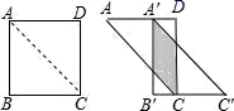17．正比例函数图象与反比例函数图象的一个交点的横坐标为，则______.三、解答题 （本大题共7小题，共64分.解答应写出文字说明、证明过程或演算步骤.）18．（5分）甲、乙两人沿同一路线登山，图中线段OC、折线OAB分别是甲、乙两人登山的路程y（米）与登山时间x（分）之间的函数图象．请根据图象所提供的信息，解答如下问题：（1）求甲登山的路程与登山时间之间的函数关系式，并写出自变量x的取值范围；（2）求乙出发后多长时间追上甲？此时乙所走的路程是多少米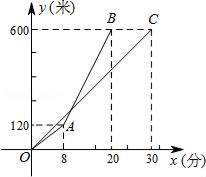？   19．（5分）如图，点E，F在菱形ABCD的对边上，AE⊥BC．∠1＝∠1．（1）判断四边形AECF的形状，并证明你的结论．（1）若AE＝4，AF＝1，试求菱形ABCD的面积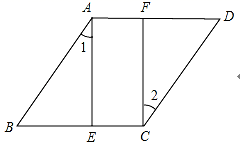．   20．（8分）为了了解同学们对垃圾分类知识的知晓程度，增强同学们的环保意识，普及垃圾分类及投放的相关知识．某校环保社团的同学们设计了“垃圾分类知识及投放情况”的问卷，并在本校随机抽取了若干名同学进行了问卷测试，根据测试成绩分布情况，他们将全部成绩分成A，B，C，D四组，并绘制了如下不完整的统计图表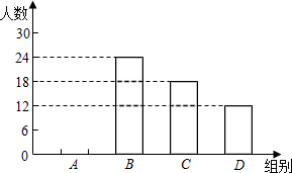：组别分数段频数频率A61≤x＜71abB71≤x＜81241．4C81≤x＜9118cD91≤x＜111121．2请根据上述统计图表，解答下列问题：（1）共抽取了多少名学生进行问卷测试？（2）补全频数分布直方图；（3）如果测试成绩不低于81分者为“优秀”，请你估计全校2111名学生中，“优秀”等次的学生约有多少人？   21．（10分） “二广”高速在益阳境内的建设正在紧张地进行，现有大量的沙石需要运输．“益安”车队有载重量为8吨、10吨的卡车共12辆，全部车辆运输一次能运输110吨沙石．（1）求“益安”车队载重量为8吨、10吨的卡车各有多少辆？（2）随着工程的进展，“益安”车队需要一次运输沙石165吨以上，为了完成任务，准备新增购这两种卡车共6辆，车队有多少种购买方案，请你一一写出．   22．（10分）如图，矩形OBCD中，OB＝5，OD＝3，以O为原点建立平面直角坐标系，点B，点D分别在x轴，y轴上，点C在第一象限内，若平面内有一动点P，且满足S△POB＝S矩形OBCD，问：（1）当点P在矩形的对角线OC上，求点P的坐标；（2）当点P到O，B两点的距离之和PO+PB取最小值时，求点P的坐标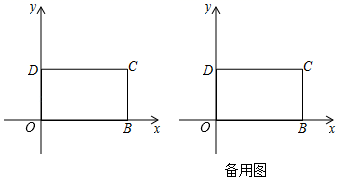．   23．（12分）银隆百货大楼服装柜在销售中发现：某品牌童装每件成本60元，现以每件100元销售，平均每天可售出20件．为了迎接“五•一”劳动节，商场决定采取适当的降价措施，以扩大销售量，增加盈利，尽量减少库存．经市场调查发现：如果每件童装降价1元，那么平均每天就可多销售2件．（1）要想平均每天销售这种童装盈利1200元，请你帮商场算一算，每件童装应定价多少元？（2）这次降价活动中，1200元是最高日利润吗？若是，请说明理由；若不是，请试求最高利润值．   参考答案 一、选择题：本大题共12个小题，每小题3分，共36分.在每小题给出的四个选项中，只有一项是符合题目要求的.1、C2、C3、B4、C5、C6、C7、C8、B9、D10、C11、D12、C 二、填空题（每题4分，满分20分，将答案填在答题纸上）13、−.14、15、3.16、1或817、4 三、解答题 （本大题共7小题，共64分.解答应写出文字说明、证明过程或演算步骤.）18、（1）y=20x（0≤x≤30）；（2）乙出发后10分钟追上甲，此时乙所走的路程是200米．19、四边形AECF是矩形，理由见解析；（1）菱形ABCD的面积＝10.20、（1）61（名）；（2）见解析；（3）估计全校2111名学生中，“优秀”等次的学生约有1111人．21、解：（1）设“益安”车队载重量为8吨、10吨的卡车分别有x辆、y辆，根据题意得：，解得：．答：“益安”车队载重量为8吨的卡车有5辆，10吨的卡车有7辆．（2）设载重量为8吨的卡车增加了z辆，依题意得：8（5+z）+10（7+6﹣z）＞165，解得：z＜．∵z≥0且为整数，∴z=0，1，2，6﹣z=6，5，1．∴车队共有3种购车方案：①载重量为8吨的卡车不购买，10吨的卡车购买6辆；②载重量为8吨的卡车购买1辆，10吨的卡车购买5辆；③载重量为8吨的卡车购买2辆，10吨的卡车购买1辆．22、（1）P（，2）；（2）（，2）或（﹣，2）23、（1）每件童装应定价80元．（2）当降价15元，即以85元销售时，最高利润值达1250元．