


沪教版 数学七年级册 《第11章图形的运动》单元测试卷(有答案)
展开沪教新版七年级上册数学《第11章 图形的运动》单元测试卷
一.选择题
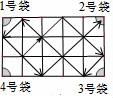
1.如图是台球桌面示意图,阴影部分表示四个入球孔,小明按图中方向击球(球可以多次反弹),则球最后落入的球袋是( )
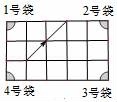
A.1号袋 B.2号袋 C.3号袋 D.4号袋
2.如图所示的网格中各有不同的图案,不能通过平移得到的是( )
A. B.
B.
C. D.
D.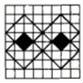
3.下列平移作图错误的是( )
A.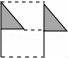 B.
B.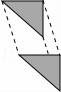 C.
C. D.
D.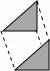
4.如图,哪一个选项的右边图形可由左边图形平移得到( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
5.学校早上8时上第一节课,45分钟后下课,这节课中分针转动的角度为( )
A.45° B.90° C.180° D.270°
6.如图,在正方形网格中有△ABC,△ABC绕O点按逆时针旋转90°后的图案应该是( )
A.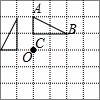 B.
B.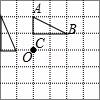
C.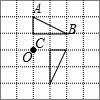 D.
D.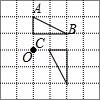
7.如图所示的图案可以看作由“基本图案”经过平移得到的是( )
A. B.
B.
C. D.
D.![]()
8.汉字“王、人、木、水、口、立”中能通过单独平移组成一个新的汉字的有( )
A.1个 B.2个 C.3个 D.4个
9.如图,将线段AB平移到线段CD的位置,则a+b的值为( )
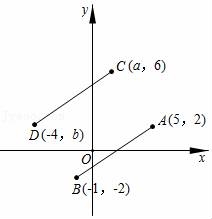
A.4 B.0 C.3 D.﹣5
10.下面的图形中必须由“基本图形”既平移又旋转而形成的图形是( )
A.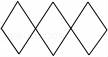 B.
B.![]()
C.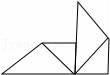 D.
D.![]()
二.填空题
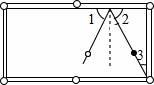
11.数学在我们的生活中无处不在,就连小小的台球桌上都有数学问题.如图所示,∠1=∠2,若∠3=30°,为了使白球反弹后能将黑球直接撞入袋中,那么击打白球时,必须保证∠1等于 .
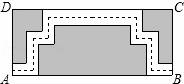
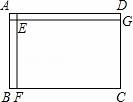
12.如图是某公园里一处矩形风景欣赏区ABCD,长AB=50米,宽BC=25米,为方便游人观赏,公园特意修建了如图所示的小路(图中非阴影部分),小路的宽均为1米,那么小明沿着小路的中间出口A到出口B所走的路线(图中虚线)长为 米.
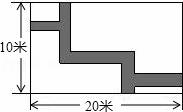
13.如图,在长20米,宽10米的长方形草地内修建了宽2米的道路,则草地的面积为 .
14.在平面直角坐标系中,小明从原点开始,按照向上平移1个单位长度描点A1,然后向右平移2个单位长度描点A2,然后向上平移2个单位长度描点A3,然后向右平移1个单位长度描点A4,之后重复上述步骤,以此类推进行描点(如图),那么她描出的点A87的坐标是 .

15.钟表分针的运动可看作是一种旋转现象,一只标准时钟的分针匀速旋转,经过12分钟旋转了 .
16.如图,照相时为了把近处的较高物体照下来,常常保持镜头中心不动,使相机旋转一定的角度,若A点从水平位置顺时针旋转了30°,那么B点从水平位置顺时针旋转了 度.

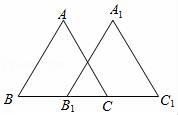
17.如图所示,将△ABC沿BC边平移得到△A1B1C1,若BC1=8,B1C=2,则平移距离为 .
18.如图,在5×5方格纸中,将图①中的三角形甲平移到图②中所示的位置,与三角形乙拼成一个矩形,那么正确的平移方法是 .
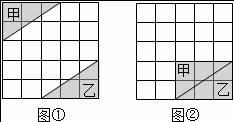
19.如图所示,某住宅小区内有一长方形地块,想在长方形地块内修筑同样宽的两条”之”字路,余下部分绿化,道路的宽为2米,则绿化的面积为 m2.
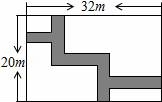
20.如图所示,在正方形网格中,图①经过 变换可以得到图②;图③是由图②经过旋转变换得到的,其旋转中心是点 (填“A”或“B”或“C”).
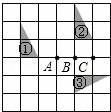
三.解答题
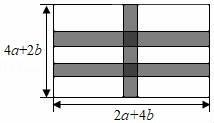
21.某校为了改善校园环境,准备在长宽如图所示的长方形空地上,修建两横纵宽度均为a米的三条小路,其余部分修建花圃.
(1)用含a,b的代数式表示花圃的面积并化简.
(2)记长方形空地的面积为S1,花圃的面积为S2,若2S2﹣S1=7b2,求![]() 的值.
的值.
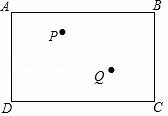
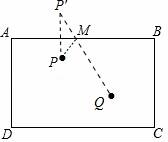
22.如图,长方形台球桌ABCD上有两个球P,Q.
(1)请画出一条路径,使得球P撞击台球桌边AB反弹后,正好撞到球Q;
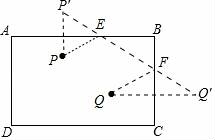
(2)请画出一条路径,使得球P撞击台球桌边,经过两次反弹后,正好撞到球Q.
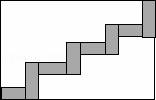
23.如图所示,一块长为18m,宽为12m的草地上有一条宽为2m的曲折的小路,求这块草地的绿地面积.
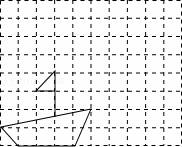
24.按要求画图:如图所示,网格内每个小正方形的边长都为1个单位长度,试画出小船向右平移4个单位长度,向上平移4个单位长度后的图形.
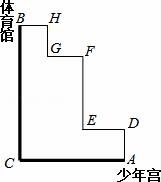
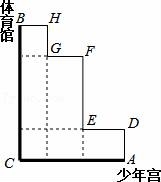
25.如图,粗线A→C→B和细线A→D→E→F→F→G→H→B是公交车从少年宫A到体育馆B的两条行驶路线.
①比较两条线路的长短(简要在下图上画出比较的痕迹);
②小丽坐出租车由体育馆B到少年宫A,假设出租车的收费标准为:起步价为7元,3千米以后每千米1.8元,用代数式表示出租车的收费m元与行驶路程s(s>3)千米之间的关系;
③如果这段路程长4.5千米,小丽身上有10元钱,够不够小丽坐出租车由体育馆到少年宫呢?说明理由.
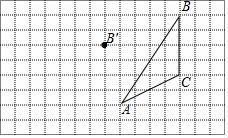
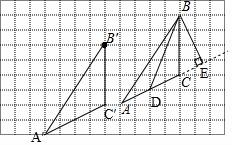
26.如图,在方格纸内将△ABC经过一次平移后得到△A′B′C′,图中标出了点B的对应点B′.根据下列条件,利用网格点和三角尺画图:
(1)补全△A′B′C′
(2)画出AC边上的中线BD;
(3)画出AC边上的高线BE;
(4)求△ABD的面积 .
27.如图1.将线段AB平移至CD,使A与D对应,B与C对应,连AD、BC.
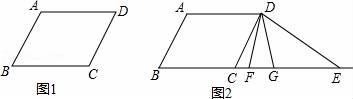
(1)填空:AB与CD的关系为 ,∠B与∠D的大小关系为
(2)如图2,若∠B=60°,F、E为BC的延长线上的点,∠EFD=∠EDF,DG平分∠CDE交BE于G,求∠FDG.
(3)在(2)中,若∠B=α,其它条件不变,则∠FDG= .
参考答案与试题解析
一.选择题
1.解:如图所示,
 ,
,
球最后落入的球袋是2号袋,
故选:B.
2.解:A、可以通过平移得到,不符合题意;
B、可以通过平移得到,不符合题意;
C、不可以通过平移得到,符合题意;
D、可以通过平移得到,不符合题意.
故选:C.
3.解:A、B、D符合平移变换,C是轴对称变换.
故选:C.
4.解:观察图形可知C中的图形是平移得到的.
故选:C.
5.解:早上8时分针指向数字12,45分钟后分针指向数字9,所以这节课中分针转动的角度为270°.
故选:D.
6.解:根据旋转的性质和旋转的方向得:△ABC绕O点按逆时针旋转90°后的图案是A,
故选:A.
7.解:A、不是由“基本图案”经过平移得到,故此选项错误;
B、不是由“基本图案”经过平移得到,故此选项错误;
C、不是由“基本图案”经过平移得到,故此选项错误;
D、是由“基本图案”经过平移得到,故此选项正确;
故选:D.
8.解:“人”平移得到“从”,“木”平移得到“林”,“水”平移得到“淼”,“口”平移得到“品”,所以通过平移组成一个新的汉字的有4个.
故选:D.
9.解:由题意,线段AB向左平移3个单位,再向上平移4个单位得到线段CD,
∴a=5﹣3=2,b=﹣2+4=2,
∴a+b=4,
故选:A.
10.解:A、只要平移即可得到,故错误;
B、只能旋转就可得到,故错误;
C、只有两个基本图形旋转得到,故错误;
D、既要平移,又要旋转后才能得到,故正确.
故选:D.
二.填空题
11.解:∵由题意可得:∠2+∠3=90°,∠3=30°,
∴∠2=60°,
∵∠1=∠2,
∴∠1=60°.
故答案为:60°.
12.解:利用已知可以得出此图形可以分为横向与纵向分析,横向距离等于AB,纵向距离等于(AD﹣1)×2,
∴图是某公园里一处矩形风景欣赏区ABCD,长AB=50米,宽BC=25米,为50+(25﹣1)×2=98米,
故答案为:98.
13.解:将道路分别向左、向上平移,得到草地为一个长方形,
长方形的长为20﹣2=18(米),宽为10﹣2=8(米),
则草地面积为18×8=144米2.
故答案为:144米2.

14.解:如图所示:A1(0,1),A2(2,1),A3(2,3),A4(3,3),A5(3,4),A6(5,4),A7(5,6),A8(6,6),A9(6,7),A10(8,7),A11(8,9),A12(9,9),
可得:A点每4个点位置分布规律相同,且A4(3,3),A8(2×3,2×3),A12(3×3,3×3),
∵87÷4=21…3,
∴A点经过21次循环后,又进行了3次变化,
∴A84(21×3,21×3),即(63,63),
∴A85(63,64),则A86(65,64),
故点A87的坐标是:(65,66).
故答案为:(65,66).
15.解:∵时钟上的分针匀速旋转一周的度数为360°,时钟上的分针匀速旋转一周需要60分钟,
则时钟上的分针匀速旋转一分钟时的度数为:360÷60=6°,
那么20分钟,分针旋转了12×6°=72°.
故答案为:72°.
16.解:B点从水平位置顺时针旋转的角度与点A相同都是30度.
17.解:∵△ABC沿BC边平移得到△A1B1C1,
∴BC=B1C1,BB1=CC1,
∵BC1=8,B1C=2,
∴BB1=CC1=![]() ,
,
即平移距离为3,
故答案为:3.
18.解:观察图形可知:正确的平移方法是向右平移2个格,再向下平移3个格(或先向下平移3个格,再向右平移2个格).
故答案为:向右平移2个格,再向下平移3个格(或先向下平移3个格,再向右平移2个格).
19.解:如图,把两条”之”字路平移到长方形地块ABCD的最上边和最左边,则余下部分EFGH是矩形.
∵CF=32﹣2=30(米),CG=20﹣2=18(米),
∴矩形EFCG的面积=30×18=540(平方米).
答:绿化的面积为540m2.
故答案为:540.
20.解:根据题意:观察可得:图①与图②对应点位置不变,通过平移可以得到;
根据旋转中心的确定方法,两组对应点连线的垂直平分线的交点,可确定图②经过旋转变换得到图③的旋转中心是A.
故答案为:平移,A.
三.解答题
21.解:(1)平移后图形为:(空白处为花圃的面积)

所以花圃的面积=(4a+2b﹣2a)(2a+4b﹣a)
=(2a+2b)(a+4b)
=2a2+8ab+2ab+8b2
=2a2+10ab+8b2;
(2)S1=(4a+2b)(2a+4b)=8a2+20ab+8b2,
S2=2a2+10ab+8b2;
∵2S2﹣S1=7b2,
∴2(2a2+10ab+8b2)﹣(8a2+20ab+8b2)=7b2,
∴b2=4a2,
∴b=2a,
∴S1=8a2+40a2+32a2=80a2,S2=2a2+20a2+32a2=54a2,
∴![]() =
=![]() =
=![]() .
.
22.解:(1)如图,运动路径:P→M→Q,点M即为所求.
(2)如图,运动路径:P→E→F→Q,点E,点F即为所求.
23.解:绿地的面积为:(18﹣2)×(12﹣2)=160(m2),
答:这块草地的绿地面积是160m2.
24.解:所作图形如下:
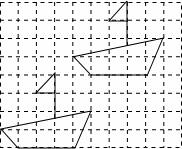 .
.
25.解:①如图所示:两条线路的长相等;
②由题意可得:m=7+1.8(s﹣3)=1.8s+1.6;
③小丽坐出租车由体育馆到少年宫,钱不够,
理由:由②得:m=1.8×5+1.6=10.6(元).
小丽坐出租车由体育馆到少年宫10元不够.
26.解:(1)如图所示,△A′B′C′即为所求作三角形.
(2)如图所示,BD为AC边上的中线;
(3)如图所示,BE为AC边上的高线;
(4)S△ABD=4×6﹣![]() ×1×2﹣
×1×2﹣![]() ×4×6﹣
×4×6﹣![]() ×(1+6)×2=24﹣1﹣12﹣7=4,
×(1+6)×2=24﹣1﹣12﹣7=4,
故答案为:4.
27.解:(1)AB∥CD,且AB=CD,∠B与∠D相等;
(2)∵AB∥CD,
∴∠DCE=∠B,
由三角形的外角性质得,∠CDF=∠DFE﹣∠DCE,
∴∠CDG=∠CDF+∠FDG=∠DFE﹣∠DCE+∠FDG,
在△DEF中,∠DEF=180°﹣2∠DFE,
在△DFG中,∠DGF=180°﹣∠FDG﹣∠DFE,
∴∠EDG=∠DGF﹣∠DEF=180°﹣∠FDG﹣∠DFE﹣(180°﹣2∠DFE)=2∠DFE﹣∠FDG﹣∠DFE,
∵DG平分∠CDE,
∴∠CDG=∠EDG,
∴∠DFE﹣∠DCE+∠FDG=2∠DFE﹣∠FDG﹣∠DFE,
∴∠FDG=![]() ∠DCE,
∠DCE,
即∠FDG=![]() ∠B,
∠B,
∵∠B=60°,
∴∠FDG=![]() ×60°=30°;
×60°=30°;
(3)思路同(2),
∵∠B=α,
∴∠FDG=![]() .
.
故答案为:(1)AB∥CD,且AB=CD,相等;(3)![]() .
.









