沪教版 数学七年级册 第10章【分式】单元基础专练

这是一份沪教版 数学七年级册 第10章【分式】单元基础专练，共13页。
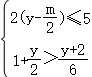【分式】单元基础专练一．选择题1．下列式子：﹣5x，，，，，其中分式有（　　）A．1个 B．2个 C．3个 D．4个2．已知a＝2b≠0，则代数式的值为（　　）A．1 B． C． D．23．如果把分式中的x、y都扩大5倍，那么分式的值（　　）A．不变 B．扩大5倍 C．缩小5倍 D．以上都不正确4．下列结论正确的是（　　）A．＝是分式方程 B．方程﹣＝1无解 C．方程＝的根为x＝0 D．解分式方程时，一定会出现增根5．下列各数中，负数是（　　）A．﹣|﹣3| B．﹣（﹣3） C．（﹣3）2 D．（﹣3）06．若a＝+1，则＝（　　）A．3 B．4 C． D．7．若代数式有意义，则实数x的取值范围是（　　）A．x＝0 B．x＝2 C．x≠0 D．x≠28．若关于x的分式方程﹣＝3的解为正整数，且关于y的不等式组至多有六个整数解，则符合条件的所有整数m的取值之和为（　　）A．1 B．0 C．5 D．69．如果x+y＝5，那么代数式（1+）÷的值为（　　）A．1 B．﹣1 C．5 D．﹣510．若分式的值为正数，则x需满足的条件是（　　）A．x为任意实数 B．x C．x D．x二．填空题11．分式的值比分式的值大3，则x的值为　   　．12．要使分式有意义，x需满足的条件是　   　．13．若不等式3x＜6的解都能使关于x的一次不等式（m﹣1）x＜m+5成立，且使关于x的分式方程＝3+有整数解，那么符合条件的所有整数m的值之和是　   　．14．计算：（﹣1）2020﹣（π﹣3.14）0的结果为　   　．15．若代数式的值为整数，则满足条件的整数x为　   　．三．解答题16．解下列方程或不等式（组）：（1）（2）2（5x+2）≤x﹣3（1﹣2x）（3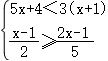），并把它的解集在数轴上表示出来．    17．（1）先化简，再求值：（1﹣）÷，其中m＝1；（2）解方程：＝3+．    18．计算：（1）16﹣（﹣17）+（﹣9）﹣14；（2）．    19．已知点A，B在数轴上所对应的数分别为，，若A，B两点关于原点对称．（1）当m＝3时，求x的值；（2）若不存在满足条件的x，求m的值．    20．阅读理解：【例】已知x+＝3，求分式的值．解：因为﹣4＝3﹣4＝﹣1，所以＝﹣1．【活学活用】（1）已知a+＝﹣5，求分式的值．（2）已知b+＝﹣3，求分式的值．（3）已知x+＝﹣5，求分式的值．
参考答案一．选择题1．解：，的分母中含有字母，属于分式，共有2个．故选：B．2．解：因为a＝2b≠0，所以＝＝＝＝＝．故选：B．3．解：分式中的x、y都扩大5倍，得＝＝，故选：A．4．解：A．原方程中分母不含未知数，不是分式方程，所以A选项不符合题意；B．解方程，得x＝﹣2，经检验x＝﹣2是原方程的增根，所以原方程无解，所以B选项符合题意；C．解方程，得x＝0，经检验x＝0是原方程的增根，所以原方程无解，所以C选项不符合题意；D．解分式方程时，不一定会出现增根，只有使分式方程分母的值为0的根是增根，所以D选项不符合题意．故选：B．5．解：A、﹣|﹣3|＝﹣3，是负数，符合题意；B、﹣（﹣3）＝3是正数，不符合题意；C、（﹣3）2＝9是正数，不符合题意；D、（﹣3）0＝1是正数，不符合题意．故选：A．6．解：原式＝＝∵a＝+1，∴原式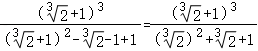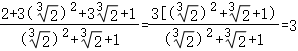＝＝．故选：A．7．解：由题意的，2﹣x≠0，解得，x≠2，故选：D．8．解：化简不等式组为，解得：﹣2＜y≤，∵不等式组至多有六个整数解，∴＜5，∴m＜5，将分式方程的两边同时乘以x﹣2，得x+m﹣1＝3（x﹣2），解得：x＝，∵分式方程的解为正整数，∴m+5是2的倍数，∵m＜5，∴m＝﹣3或m＝﹣1或m＝1或m＝3，∵x≠2，∴≠2，∴m≠﹣1，∴m＝﹣3或m＝1或m＝3，∴符合条件的所有整数m的取值之和为1，故选：A．9．解：原式＝（+）•，＝•，＝x+y，∵x+y＝5，∴原式＝5，故选：C．10．解：∵分式的值为正数，x2+3恒为正数，∴2x﹣1＞0，∴x＞．故选：C．二．填空题11．解：根据题意得：﹣＝3，去分母得：x﹣3﹣1＝3x﹣6，移项合并得：﹣2x＝﹣2，解得：x＝1，经检验x＝1是分式方程的解，故答案为：1．12．解：当x﹣1≠0时，分式有意义，∴x≠1，故答案为x≠1．13．解：∵3x＜6∴x＜2∵不等式3x＜6的解都能使关于x的一次不等式（m﹣1）x＜m+5成立∴关于x的一次不等式（m﹣1）x＜m+5的解集是x＜∴≥2∵m是整数∴m＝2，3，4，5，6，7∵＝3+∴mx＝3x﹣18+4x∴x＝∵＝3+有整数解∴m＝2，x＝，舍去；m＝3，x＝，舍去；m＝4，x＝6，是增根，舍去；m＝5，x＝9；m＝6，x＝18；m＝7，x无解，舍去；∴5+6＝11故答案为：11．14．解：（﹣1）2020﹣（π﹣3.14）0＝1﹣1＝0．故答案为：0．15．解：原式＝＝2﹣当x＝0时，原式＝1当x＝﹣2时，原式＝3则满足条件的整数x有0和﹣2．故答案为：0，﹣2．三．解答题16．解：（1）去分母得：x﹣3+x﹣2＝﹣3，解得：x＝1，经检验x＝1是分式方程的解；（2）去括号得：10x+4≤x﹣3+6x，解得：x≤﹣；（3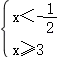），此方程组无解．17．解：（1）原式＝，＝，＝．当m＝1时，原式＝＝﹣；（2）去分母得：1＝3x﹣9﹣x，解得：x＝5，经检验x＝5是分式方程的解．18．解：（1）16﹣（﹣17）+（﹣9）﹣14＝16+17﹣9﹣14＝10； （2）原式＝﹣1+4+1＝4．19．解：根据题意得：+＝0，（1）把m＝3代入得：+＝0，去分母得：3+2x﹣7＝0，解得：x＝2，经检验x＝2是分式方程的解；（2）去分母得：m+2x﹣7＝0，由不存在满足条件x的值，得到x＝3，把x＝3代入得：m+6﹣7＝0，解得：m＝1．20．解：（1）∵a+＝﹣5，∴＝2a+5+＝2（a+）+5＝2×（﹣5）+5＝﹣5； （2）∵b+＝﹣3，∴＝3b﹣4+＝3（b+）﹣4＝3×（﹣3）﹣4＝﹣13，∴＝﹣；  （3）∵x+＝﹣5，∴＝＝x+1﹣3+＝x+﹣2＝﹣5﹣2＝﹣7，∴．