初中数学华师大版八年级上册2 幂的乘方优秀学案设计

2.幂的乘方

学习目标：1.理解并掌握幂的乘方法则.（重点）

2.会运用幂的乘方法则进行幂的乘方的运算.（难点）

自主学习

一、知识链接

1.同底数幂的乘法法则：am·an=_____.

2. 计算：

(1) 73×75 =________；                 (2)a6·a2 =________； 

(3) x2·x3·x4 =________；          (4)(－x)3·(－x)5=________ .

二、新知预习

填一填：根据乘方的意义及同底数幂的乘法法则填空：

  (1)  (43)2=43·43=4（   ） ;     (2)  (52)3= （   ）·（   ）·（   ）=5（   ）.

合作探究

一、探究过程

探究点1： 幂的乘方运算

试一试：根据“填一填”中的形式填空：(a3)4=             =a（   ）.

【要点归纳】(am)n = ________  (m、n是正整数)，即幂的乘方，底数_________，指数________.

思考：(-a2)5和(-a5)2的结果相同吗?为什么?

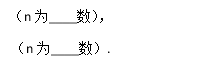
【要点归纳】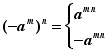

例1计算：

(1) (x4)3；                          (2)(-a2)7.

【针对训练】计算： (1)(x3)6；    (2)[(a－b)4]5；21世纪教育网       (3)-(-x3)2·(x3)4.

探究点2：幂的乘方法则的逆用

例2已知10m＝3，10n＝2，求下列各式的值.

     (1)103m；    (2)102n；    (3)103m＋2n．

【方法总结】此类题的关键是逆用幂的乘方及同底数幂法则，将所求代数式正确变形，然后代入已知条件求值即可.

【针对训练】已知x2n＝3，求(x3n)4的值.

二、课堂小结

幂的乘方：数学语言：(am)n = ________  (m、n是正整数)；

          文字语言：幂的乘方，底数_________，指数________.

当堂检测

1．计算(x4)2的结果是                        (     )

A．x6    B．x8       C．x16      D．2x4

2．在下列各式的括号内，应填入b4的是(     )

A．b12＝(　　)8         B．b12＝(　　)6       C．b12＝(　　)3         D．b12＝(　　)2

3．下列计算中，错误的是(      )

A．[(a＋b)2]3＝(a＋b)6    B．[(a＋b)2]5＝(a＋b)7

C．[(a－b)3]n＝(a－b)3n    D．[(a－b)3]2＝(a－b)6

4．如果(9n)2＝312，那么n的值是(      )

A．43    B．34        C．23      D．1

5.计算：

(1)(22)4=________;  (2)(xm)2=________;(3)(－a7)4=________.

6．计算：

(1)(102)8；            (2)(xm+2)2；            (3)[(－a)3]5；      (4)－(x2)m.

7.已知3x+4y-5=0,求27x·81y的值.

参考答案

自主学习

一、知识链接

1. am+n  2.(1) 78         (2)a8     (3) x9       (4)x 8    

二、新知预习

填一填：(1)6   (2)52     52    52     6

合作探究     

一、探究过程         

探究点1：

试一试：a3·a3 · a3· a3       12  

【要点归纳】amn     不变     相乘

思考：解：不相同，前者结果是-a10，后者结果是a10.

【要点归纳】偶    奇

例1  解：（1）原式=x12.     （2）原式=-a14. 

【针对训练】

(1)原式=x18     (2)原式=(a－b)20 .    (3) 原式=-x18.教育

探究点2：

例2  解：（1）原式=（10m）3=27.   （2）原式=（10n）2=22=4.   （3）原式=103m×102n=27×4=108.

【针对训练】 解：(x3n)4=（x2n)6=36.

二、课堂小结  

 amn    不变    相乘

当堂检测    

1．B  2．C  3．B   4．B

5.解：（1）28    （2）x2m   （3）a28

6.解：（1）原式=1016.    (2) 原式=x2m+4.   (3) 原式= －a15 .     (4) 原式=－x2m.

7.解：因为3x+4y-5=0,所以3x+4y=5.所以27x·81y= 33x+4y=35.