


四川成都市武侯区西蜀实验学校2022-2023学年七下数学期末统考试题含答案
展开四川成都市武侯区西蜀实验学校2022-2023学年七下数学期末统考试题
(时间:120分钟 分数:120分)
学校_______ 年级_______ 姓名_______
注意事项:
1.答题前,考生先将自己的姓名、准考证号码填写清楚,将条形码准确粘贴在条形码区域内。
2.答题时请按要求用笔。
3.请按照题号顺序在答题卡各题目的答题区域内作答,超出答题区域书写的答案无效;在草稿纸、试卷上答题无效。
4.作图可先使用铅笔画出,确定后必须用黑色字迹的签字笔描黑。
5.保持卡面清洁,不要折暴、不要弄破、弄皱,不准使用涂改液、修正带、刮纸刀。
一、选择题(每小题3分,共30分)
1.点A(1,-2)在正比例函数![]() 的图象上,则k的值是( ).
的图象上,则k的值是( ).
A.1 B.-2 C.![]() D.
D.![]()
2.一组数据5,8,8,12,12,12,44的众数是( )
A.5 B.8 C.12 D.44
3.设![]() ,a在两个相邻整数之间,则这两个整数是( )
,a在两个相邻整数之间,则这两个整数是( )
A.1和2 B.2和3 C.3和4 D.4和5
4.若一个三角形的三边长为![]() ,则使得此三角形是直角三角形的的值是( )
,则使得此三角形是直角三角形的的值是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 或
或![]()
5.下列给出的四个点中,不在直线y=2x-3上的是 ( )
A.(1, -1) B.(0, -3) C.(2, 1) D.(-1,5)
6.在下列四组数中,不是勾股数的一组数是( )
A.a=15,b=8,c=17 B.a=9,b=12,c=15 C.a=7,b=24,c=25 D.a=3,b=5,c=7
7.有m支球队参加篮球比赛,共比赛了21场,每两队之间都比赛一场,则下列方程中符合题意的是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
8.如果点![]() 在正比例函数
在正比例函数![]() 的图像上,那么下列等式一定成立的是( )
的图像上,那么下列等式一定成立的是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
9.具备下列条件的三角形中,不是直角三角形的是( )
A.∠A+∠B=∠C B.∠B=∠C=![]() ∠A
∠A
C.∠A=90°-∠B D.∠A-∠B=90°
10.若b>0,则一次函数y=﹣x+b的图象大致是( )
A. B.
B.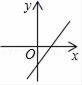 C.
C.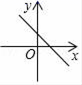 D.
D.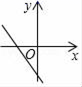
二、填空题(本大题共有6小题,每小题3分,共18分)
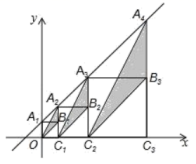
11.在直角坐标系中,直线![]() 与y轴交于点
与y轴交于点![]() ,按如图方式作正方形
,按如图方式作正方形![]() 、
、![]() 、
、![]() …,
…,![]() 、
、![]() 、
、![]() …在直线
…在直线![]() 上,点
上,点![]() 、
、![]() 、
、![]() …,在x轴上,图中阴影部分三角形的面积从左到右依次记为
…,在x轴上,图中阴影部分三角形的面积从左到右依次记为![]() 、
、![]() 、
、![]() 、..
、..![]() ,则
,则![]() 的值为________.
的值为________.
12.如图,在平面直角坐标系xOy中,已知正比例函数y= -2x和反比例函数![]() 的图象交于A(a,-4),B两点。过原点O的另一条直线l与双曲线
的图象交于A(a,-4),B两点。过原点O的另一条直线l与双曲线![]() 交于点P,Q两点(P点在第二象限),若以点A,B,P,Q为顶点的四边形面积为24,则点P的坐标是_______
交于点P,Q两点(P点在第二象限),若以点A,B,P,Q为顶点的四边形面积为24,则点P的坐标是_______

13.计算:![]() ____.
____.
14.已知不等式组![]() 的解集为
的解集为![]() ,则
,则![]() 的值是________.
的值是________.
15.已知直线y=﹣![]() 与x轴、y轴分别交于点A、B,在坐标轴上找点P,使△ABP为等腰三角形,则点P的个数为_____个.
与x轴、y轴分别交于点A、B,在坐标轴上找点P,使△ABP为等腰三角形,则点P的个数为_____个.
16.已知点P(m-3,m+1)在第二象限,则m的取值范围是_______________.
三、解下列各题(本大题共8小题,共72分)
17.(8分)如图,分别以![]() 的边向外作正方形ABFG和ACDE,连接EG,若O为EG的中点,
的边向外作正方形ABFG和ACDE,连接EG,若O为EG的中点,
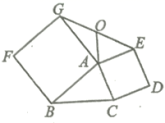
求证:(1)![]() ;
;
(2)![]() .
.
18.(8分)在直角坐标系中,直线l1经过(2,3)和(-1,-3):直线l2经过原点O,且与直线l1交于点P(-2,a).
(1)求a的值;
(2)(-2,a)可看成怎样的二元一次方程组的解?
19.(8分)如图,![]() 中,
中,![]() ,
,![]() 是
是![]() 上一点,
上一点,![]() 于点
于点![]() ,
,![]() 是
是![]() 的中点,
的中点,![]() 于点
于点![]() ,与
,与![]() 交于点
交于点![]() ,若
,若![]() ,
,![]() 平分
平分![]() ,连结
,连结![]() ,
,![]() .
.

(1)求证:![]() ;
;
(2)求证:![]() .
.
(3)若![]() ,判定四边形
,判定四边形![]() 是否为菱形,并说明理由.
是否为菱形,并说明理由.
20.(8分)某中学为了预防流行性感冒,对教室采用药熏消毒法进行消毒,已知药物燃烧时,室内每立方米空气中的含药量![]() 与时间
与时间![]() 成正比例.药物燃烧后,y与x成反比例(如图所示),现测得药物6min燃毕,此时室内空气中每立方米的含药量为4mg,
成正比例.药物燃烧后,y与x成反比例(如图所示),现测得药物6min燃毕,此时室内空气中每立方米的含药量为4mg,
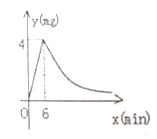
(1)写出药物燃烧前后,y与x之间的函数表达式;
(2)研究表明,当空气中每立方米的含药量低于1.6mg时学生方可进教室,那么从消毒开始,至少需要经过多少分钟,学生方能回到教室?
(3)研究表明,当空气中每立方米的含药量不低于2mg且持续时间不低于9min时,才能有效杀灭空气中的病菌,那么此次消毒是否有效?
21.(8分)某部队将在指定山区进行军事演习,为了使道路便于部队重型车辆通过,部队工兵连接到抢修一段长3600米道路的任务,按原计划完成总任务的![]() 后,为了让道路尽快投入使用,工兵连将工作效率提高了50%,一共用了10小时完成任务.
后,为了让道路尽快投入使用,工兵连将工作效率提高了50%,一共用了10小时完成任务.
(1)按原计划完成总任务的![]() 时,已抢修道路 米;
时,已抢修道路 米;
(2)求原计划每小时抢修道路多少米?
22.(10分)在平面直角坐标系中,过点C(1,3)、D(3,1)分别作x轴的垂线,垂足分别为A、B.
(1)求直线CD和直线OD的解析式;
(2)点M为直线OD上的一个动点,过M作x轴的垂线交直线CD于点N,是否存在这样的点M,使得以A、C、M、N为顶点的四边形为平行四边形?若存在,求此时点M的横坐标;若不存在,请说明理由;
(3)若△AOC沿CD方向平移(点C在线段CD上,且不与点D重合),在平移的过程中,设平移距离为![]() t,△AOC与△OBD重叠部分的面积记为s,试求s与t的函数关系式.
t,△AOC与△OBD重叠部分的面积记为s,试求s与t的函数关系式.

23.(10分)已知,在矩形![]() 中,
中,![]() 的平分线DE交BC边于点E,点P在线段DE上(其中EP<PD).
的平分线DE交BC边于点E,点P在线段DE上(其中EP<PD).

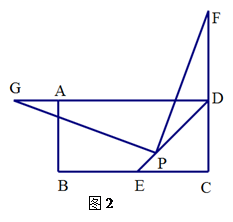
(1)如图1,若点F在CD边上(不与点C,D重合),将![]() 绕点P逆时针旋转90°后,角的两边PD、PF分别交AD边于点H、G.
绕点P逆时针旋转90°后,角的两边PD、PF分别交AD边于点H、G.
①求证:![]() ;
;
②探究:![]() 、
、![]() 、
、![]() 之间有怎样的数量关系,并证明你的结论;
之间有怎样的数量关系,并证明你的结论;
(2)拓展:如图2,若点F在CD的延长线上,过点P作![]() ,交射线DA于点G.你认为(2)中DF、DG、DP之间的数量关系是否仍然成立?若成立,给出证明,若不成立,请写出它们所满足的数量关系式,并说明理由.
,交射线DA于点G.你认为(2)中DF、DG、DP之间的数量关系是否仍然成立?若成立,给出证明,若不成立,请写出它们所满足的数量关系式,并说明理由.
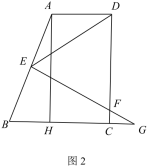
24.(12分)如图,已知直角梯形![]() ,
,![]() ,
,![]() ,过点
,过点![]() 作
作![]() ,垂足为点
,垂足为点![]() ,
,![]() ,
,![]() ,点
,点![]() 是
是![]() 边上的一动点,过
边上的一动点,过![]() 作线段
作线段![]() 的垂直平分线,交
的垂直平分线,交![]() 于点
于点![]() ,并交射线
,并交射线![]() 于点
于点![]() .
.
(1)如图1,当点![]() 与点
与点![]() 重合时,求
重合时,求![]() 的长;
的长;
(2)设![]() ,
,![]() ,求
,求![]() 与
与![]() 的函数关系式,并写出定义域;
的函数关系式,并写出定义域;
(3)如图2,联结![]() ,当
,当![]() 是等腰三角形时,求
是等腰三角形时,求![]() 的长.
的长.


参考答案
一、选择题(每小题3分,共30分)
1、B
2、C
3、C
4、D
5、D
6、D
7、A
8、D
9、D
10、C
二、填空题(本大题共有6小题,每小题3分,共18分)
11、![]()
12、P(﹣4,2)或P(﹣1,8).
13、1
14、![]()
15、1
16、﹣1<m<1
三、解下列各题(本大题共8小题,共72分)
17、(1)证明见详解;(2)证明见详解.
18、(1)a=-5;(2)可以看作二元一次方程组![]() 的解.
的解.
19、(1)见解析;(2)证明见解析;(3)四边形AEGF是菱形,证明见解析.
20、(1)药物燃烧时y关于x的函数关系式为:![]() ;药物燃烧后y关于x的函数关系式为:
;药物燃烧后y关于x的函数关系式为:![]() ;(2)至少需要15分钟后学生方能回到教室;(3)此次消毒有效.
;(2)至少需要15分钟后学生方能回到教室;(3)此次消毒有效.
21、(1)1200;(2)1.
22、(1)直线OD的解析式为y=![]() x;(2)存在.满足条件的点M的横坐标
x;(2)存在.满足条件的点M的横坐标![]() 或
或![]() ,理由见解析;(3)S=﹣
,理由见解析;(3)S=﹣![]() (t﹣1)2+
(t﹣1)2+![]() .
.
23、(1)①详见解析;②![]() ,详见解析;(2)
,详见解析;(2)![]() .详见解析
.详见解析
24、(1)BC=5;(2)![]() ;(3)
;(3)![]() 的长为
的长为![]() 或3或
或3或![]() .
.
四川省成都市武侯区西蜀实验学校2023-2024学年九上数学期末检测模拟试题含答案: 这是一份四川省成都市武侯区西蜀实验学校2023-2024学年九上数学期末检测模拟试题含答案,共7页。试卷主要包含了考生必须保证答题卡的整洁,下列说法中正确的是,下列说法错误的是,若,,则的值为等内容,欢迎下载使用。
四川省成都市武侯区西蜀实验学校2023-2024学年九上数学期末质量跟踪监视试题含答案: 这是一份四川省成都市武侯区西蜀实验学校2023-2024学年九上数学期末质量跟踪监视试题含答案,共7页。试卷主要包含了考生必须保证答题卡的整洁,抛物线y=3,抛物线的对称轴是直线,方程2x等内容,欢迎下载使用。
2023-2024学年四川成都市武侯区西蜀实验学校数学九上期末教学质量检测试题含答案: 这是一份2023-2024学年四川成都市武侯区西蜀实验学校数学九上期末教学质量检测试题含答案,共8页。












