


四川省成都市成都外国语学校2022-2023学年数学七下期末调研试题含答案
展开
这是一份四川省成都市成都外国语学校2022-2023学年数学七下期末调研试题含答案,共8页。试卷主要包含了在平面直角坐标系中,点等内容,欢迎下载使用。
四川省成都市成都外国语学校2022-2023学年数学七下期末调研试题(时间:120分钟 分数:120分) 学校_______ 年级_______ 姓名_______ 考生须知:1.全卷分选择题和非选择题两部分,全部在答题纸上作答。选择题必须用2B铅笔填涂;非选择题的答案必须用黑色字迹的钢笔或答字笔写在“答题纸”相应位置上。2.请用黑色字迹的钢笔或答字笔在“答题纸”上先填写姓名和准考证号。3.保持卡面清洁,不要折叠,不要弄破、弄皱,在草稿纸、试题卷上答题无效。 一、选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.以下各组数中,能作为直角三角形的三边长的是![]()
![]() A.6,6,7 B.6,7,8 C.6,8,10 D.6,8,92.如图:菱形ABCD的对角线AC,BD相交于点O,AC=
A.6,6,7 B.6,7,8 C.6,8,10 D.6,8,92.如图:菱形ABCD的对角线AC,BD相交于点O,AC=![]() ,BD=
,BD=![]() ,动点P在线段BD上从点B向点D运动,PF⊥AB于点F,PG⊥BC于点G,四边形QEDH与四边形PFBG关于点O中心对称,设菱形ABCD被这两个四边形盖住部分的面积为S1,未被盖住部分的面积为S2,
,动点P在线段BD上从点B向点D运动,PF⊥AB于点F,PG⊥BC于点G,四边形QEDH与四边形PFBG关于点O中心对称,设菱形ABCD被这两个四边形盖住部分的面积为S1,未被盖住部分的面积为S2,![]() ,若S1=S2,则
,若S1=S2,则![]() 的值是( )
的值是( )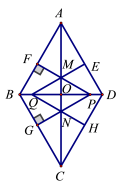 A.
A.![]() B.
B.![]() 或
或![]() C.
C.![]() D.不存在3.用一长一短的两根木棒,在它们的中心处固定一个小螺钉,做成一个可转动的叉形架,四个顶点用橡皮筋连成一个四边形,转动木条,这个四边形变成菱形时,两根木棒所成角的度数是( )A.90° B.60° C.45° D.30°4.无理数
D.不存在3.用一长一短的两根木棒,在它们的中心处固定一个小螺钉,做成一个可转动的叉形架,四个顶点用橡皮筋连成一个四边形,转动木条,这个四边形变成菱形时,两根木棒所成角的度数是( )A.90° B.60° C.45° D.30°4.无理数![]() 在两个整数之间,下列结论正确的是( )A.2~3之间 B.3~4之间 C.4~5之间 D.5~6之间5.直角梯形的一个内角为
在两个整数之间,下列结论正确的是( )A.2~3之间 B.3~4之间 C.4~5之间 D.5~6之间5.直角梯形的一个内角为![]() ,较长的腰为6
,较长的腰为6![]() ,一底为5
,一底为5![]() ,则这个梯形的面积为( )A.
,则这个梯形的面积为( )A.![]() B.
B.![]() C.25
C.25![]() D.
D.![]() 或
或![]() 6.如图,点P是双曲线y=
6.如图,点P是双曲线y=![]() (x>0)上的一个动点,过点P作PA⊥x轴于点A,当点P从左向右移动时,△OPA的面积( )
(x>0)上的一个动点,过点P作PA⊥x轴于点A,当点P从左向右移动时,△OPA的面积( )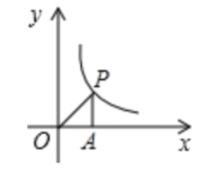 A.逐渐变大 B.逐渐变小 C.先增大后减小 D.保持不变7.如图,矩形ABCD的边长AD=3,AB=2,E为AB的中点,F在边BC上,且BF=2FC,AF分别与DE、DB相交于点M,N,则MN的长为( )
A.逐渐变大 B.逐渐变小 C.先增大后减小 D.保持不变7.如图,矩形ABCD的边长AD=3,AB=2,E为AB的中点,F在边BC上,且BF=2FC,AF分别与DE、DB相交于点M,N,则MN的长为( )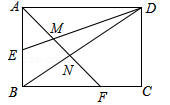 A.
A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 8.在平面直角坐标系中,点(﹣2,0)所在的位置是( )A.y轴 B.x轴 C.原点 D.二象限9.某青年排球队12名队员的年龄情况如下表所示:
8.在平面直角坐标系中,点(﹣2,0)所在的位置是( )A.y轴 B.x轴 C.原点 D.二象限9.某青年排球队12名队员的年龄情况如下表所示: 这12名队员的平均年龄是( )A.18岁 B.19岁 C.20岁 D.21岁10.如图,矩形ABCD的顶点A,C分别在直线a,b上,且a∥b,∠1=50°,则∠2的度数为( )
这12名队员的平均年龄是( )A.18岁 B.19岁 C.20岁 D.21岁10.如图,矩形ABCD的顶点A,C分别在直线a,b上,且a∥b,∠1=50°,则∠2的度数为( )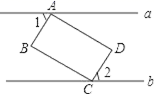 A.30° B.40° C.50° D.60°11.张浩调查统计了他们家5月份每次打电话的通话时长,并将统计结果进行分组(每组含量最小值,不含最大值),将分组后的结果绘制成如图所示的频数分布直方图,则下列说法中不正确的是( )
A.30° B.40° C.50° D.60°11.张浩调查统计了他们家5月份每次打电话的通话时长,并将统计结果进行分组(每组含量最小值,不含最大值),将分组后的结果绘制成如图所示的频数分布直方图,则下列说法中不正确的是( )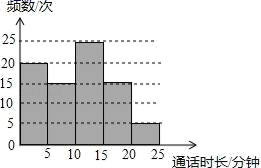 A.张浩家5月份打电话的总频数为80次B.张浩家5月份每次打电话的通话时长在5﹣10分钟的频数为15次C.张浩家5月份每次打电话的通话时长在10﹣15分钟的频数最多D.张浩家5月份每次打电话的通话时长在20﹣25分钟的频率为6%12.在同一坐标系中,一次函数y=ax+2与二次函数y=x2+a的图象可能是( )A.
A.张浩家5月份打电话的总频数为80次B.张浩家5月份每次打电话的通话时长在5﹣10分钟的频数为15次C.张浩家5月份每次打电话的通话时长在10﹣15分钟的频数最多D.张浩家5月份每次打电话的通话时长在20﹣25分钟的频率为6%12.在同一坐标系中,一次函数y=ax+2与二次函数y=x2+a的图象可能是( )A.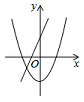 B.
B.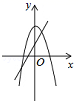 C.
C.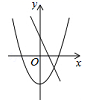 D.
D.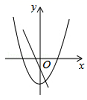 二、填空题(每题4分,满分20分,将答案填在答题纸上)13.对于非零的两个实数a、b,规定a⊕b=
二、填空题(每题4分,满分20分,将答案填在答题纸上)13.对于非零的两个实数a、b,规定a⊕b=![]() ,若2⊕(2x﹣1)=1,则x的值为 .14.在△ABC中,AB=
,若2⊕(2x﹣1)=1,则x的值为 .14.在△ABC中,AB=![]() ,AC=5,若BC边上的高等于3,则BC边的长为_____.15.如图,在
,AC=5,若BC边上的高等于3,则BC边的长为_____.15.如图,在![]() 中,
中,![]() ,
,![]() 垂足为
垂足为![]() ,
,![]() 是中线,将
是中线,将![]() 沿直线BD翻折后,点C落在点E,那么AE为_________.
沿直线BD翻折后,点C落在点E,那么AE为_________.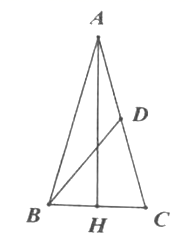 16.如图,在▱ABCD中,AB=10,BC=6,AC⊥BC,则▱ABCD的面积为_____.
16.如图,在▱ABCD中,AB=10,BC=6,AC⊥BC,则▱ABCD的面积为_____.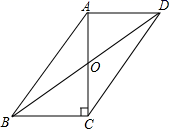 17.将直线
17.将直线![]() 沿y轴向上平移5个单位长度后,所得图象对应的函数关系式为_________.三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)18.(5分)随着信息技术的迅猛发展,人们去商场购物的支付方式更加多样、便捷,在一次购物中,张华和李红都想从“微信”、“支付宝”、“银行卡”、“现金”四种支付方式中选一种方式进行支付.(1)张华用“微信”支付的概率是______.(2)请用画树状图或列表法求出两人恰好选择同一种支付方式的概率.(其中“微信”、“支付宝”、“银行卡”、“现金”分别用字母“A”“B”“C”“D”代替) 19.(5分)在Rt△ABC中,∠C=90°,AC=6,BC=1.在CB上找一点E,使EB=EA(利用尺规作图,保留作图痕迹),并求出此时CE的长.
沿y轴向上平移5个单位长度后,所得图象对应的函数关系式为_________.三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)18.(5分)随着信息技术的迅猛发展,人们去商场购物的支付方式更加多样、便捷,在一次购物中,张华和李红都想从“微信”、“支付宝”、“银行卡”、“现金”四种支付方式中选一种方式进行支付.(1)张华用“微信”支付的概率是______.(2)请用画树状图或列表法求出两人恰好选择同一种支付方式的概率.(其中“微信”、“支付宝”、“银行卡”、“现金”分别用字母“A”“B”“C”“D”代替) 19.(5分)在Rt△ABC中,∠C=90°,AC=6,BC=1.在CB上找一点E,使EB=EA(利用尺规作图,保留作图痕迹),并求出此时CE的长.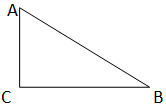 20.(8分)某社区准备在甲乙两位射箭爱好者中选出一人参加集训,两人各射了5箭,他们的总成绩(单位:环)相同,小宇根据他们的成绩绘制了尚不完整的统计图表,并计算了甲成绩的平均数和方差(见小宇的作业).
20.(8分)某社区准备在甲乙两位射箭爱好者中选出一人参加集训,两人各射了5箭,他们的总成绩(单位:环)相同,小宇根据他们的成绩绘制了尚不完整的统计图表,并计算了甲成绩的平均数和方差(见小宇的作业).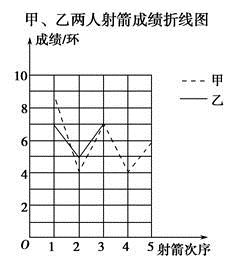 小宇的作业:
小宇的作业:
解:![]() 甲=
甲=![]() (9+4+7+4+6)=6,
(9+4+7+4+6)=6,
s甲2=![]() [(9-6)2+(4-6)2+(7-6)2+(4-6)2+(6-6)2]
[(9-6)2+(4-6)2+(7-6)2+(4-6)2+(6-6)2]
=![]() (9+4+1+4+0)
(9+4+1+4+0)
=3.6
甲、乙两人射箭成绩统计表
第1次
第2次
第3次
第4次
第5次
甲成绩
9
4
7
4
6
乙成绩
7
5
7
a
7
(1)a=________,![]() 乙=________;(2)请完成图中表示乙成绩变化情况的折线;(3)①观察图,可看出________的成绩比较稳定(填“甲”或“乙”).参照小宇的计算方法,计算乙成绩的方差,并验证你的判断.②请你从平均数和方差的角度分析,谁将被选中. 21.(10分)在平面直角坐标系
乙=________;(2)请完成图中表示乙成绩变化情况的折线;(3)①观察图,可看出________的成绩比较稳定(填“甲”或“乙”).参照小宇的计算方法,计算乙成绩的方差,并验证你的判断.②请你从平均数和方差的角度分析,谁将被选中. 21.(10分)在平面直角坐标系![]() 中,已知一次函数
中,已知一次函数![]() 的图像与
的图像与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]()
![]() 求
求![]() 两点的坐标
两点的坐标![]() 在给定的平面直角坐标系中画出该函数的图象;
在给定的平面直角坐标系中画出该函数的图象;![]() 根据图像回答:当
根据图像回答:当![]() 时,
时,![]() 的取值范围是 .
的取值范围是 .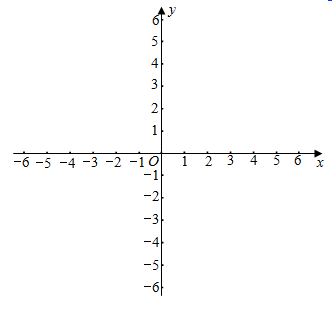 22.(10分)制作一种产品,需先将材料加热达到60℃后,再进行操作,设该材料温度为y(℃)从加热开始计算的时间为x(min).据了解,当该材料加热时,温度y与时间x成一次函数关系:停止加热进行操作时,温度y与时间x成反比例关系(如图).已知在操作加热前的温度为15℃,加热5分钟后温度达到60℃.(1)分别求出将材料加热和停止加热进行操作时,y与x的函数关系式;(2)根据工艺要求,当材料的温度低于15℃时,须停止操作,那么从开始加热到停止操作,共经历了多少时间?
22.(10分)制作一种产品,需先将材料加热达到60℃后,再进行操作,设该材料温度为y(℃)从加热开始计算的时间为x(min).据了解,当该材料加热时,温度y与时间x成一次函数关系:停止加热进行操作时,温度y与时间x成反比例关系(如图).已知在操作加热前的温度为15℃,加热5分钟后温度达到60℃.(1)分别求出将材料加热和停止加热进行操作时,y与x的函数关系式;(2)根据工艺要求,当材料的温度低于15℃时,须停止操作,那么从开始加热到停止操作,共经历了多少时间?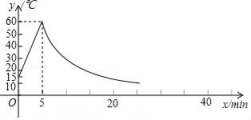 23.(12分)中国经济的快速发展让众多国家感受到了威胁,随着钓鱼岛事件、南海危机、萨德入韩等一系列事件的发生,国家安全一再受到威胁,所谓“国家兴亡,匹夫有责”,某校积极开展国防知识教育,九年级甲、乙两班分别选5名同学参加“国防知识”比赛,其预赛成绩如图所示:(1)根据上图填写下表: 平均数 中位数 众数 甲班 8.5 8.5 乙班 8.5 10(2)分别求甲乙两班的方差,并从稳定性上分析哪个班的成绩较好.
23.(12分)中国经济的快速发展让众多国家感受到了威胁,随着钓鱼岛事件、南海危机、萨德入韩等一系列事件的发生,国家安全一再受到威胁,所谓“国家兴亡,匹夫有责”,某校积极开展国防知识教育,九年级甲、乙两班分别选5名同学参加“国防知识”比赛,其预赛成绩如图所示:(1)根据上图填写下表: 平均数 中位数 众数 甲班 8.5 8.5 乙班 8.5 10(2)分别求甲乙两班的方差,并从稳定性上分析哪个班的成绩较好.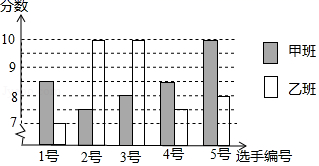 参考答案 一、选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.1、C2、A3、A4、B5、D6、D7、B8、B9、C10、C11、D12、C 二、填空题(每题4分,满分20分,将答案填在答题纸上)13、
参考答案 一、选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.1、C2、A3、A4、B5、D6、D7、B8、B9、C10、C11、D12、C 二、填空题(每题4分,满分20分,将答案填在答题纸上)13、![]() .14、9或115、
.14、9或115、![]() 16、1.17、
16、1.17、![]() 三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)18、 (1)
三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)18、 (1)![]() ;(2)
;(2)![]() .19、CE=
.19、CE=![]() 20、(1)4 6 (2)见解析 (3)①乙 1.6,判断见解析 ②乙,理由见解析21、(1)
20、(1)4 6 (2)见解析 (3)①乙 1.6,判断见解析 ②乙,理由见解析21、(1)![]() ;(1)见解析;(3)
;(1)见解析;(3)![]() 22、(1)
22、(1)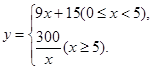 ;(2)20分钟.23、(1)甲众数:8.5,乙中位数:8;(2)甲班的成绩较好.
;(2)20分钟.23、(1)甲众数:8.5,乙中位数:8;(2)甲班的成绩较好.
相关试卷
这是一份成都市教科院附属学校2022-2023学年数学七下期末调研试题含答案,共6页。试卷主要包含了点关于y轴对称的点的坐标是,下列分解因式正确的是等内容,欢迎下载使用。
这是一份四川省成都市外国语学校2022-2023学年数学七下期末考试模拟试题含答案,共7页。试卷主要包含了正十边形的每一个内角的度数为,若正比例函数的图象经过点,定义一种正整数“”的运算,如图,点A坐标为等内容,欢迎下载使用。
这是一份四川省成都市实验外国语学校2022-2023学年数学七下期末质量跟踪监视模拟试题含答案,共7页。试卷主要包含了答题时请按要求用笔等内容,欢迎下载使用。








