


四川省达州市达川区2022-2023学年七年级数学第二学期期末联考模拟试题含答案
展开
这是一份四川省达州市达川区2022-2023学年七年级数学第二学期期末联考模拟试题含答案,共6页。试卷主要包含了下列分解因式,正确的是等内容,欢迎下载使用。
四川省达州市达川区2022-2023学年七年级数学第二学期期末联考模拟试题(时间:120分钟 分数:120分) 学校_______ 年级_______ 姓名_______ 注意事项:1. 答题前,考生先将自己的姓名、准考证号填写清楚,将条形码准确粘贴在考生信息条形码粘贴区。2.选择题必须使用2B铅笔填涂;非选择题必须使用0.5毫米黑色字迹的签字笔书写,字体工整、笔迹清楚。3.请按照题号顺序在各题目的答题区域内作答,超出答题区域书写的答案无效;在草稿纸、试题卷上答题无效。4.保持卡面清洁,不要折叠,不要弄破、弄皱,不准使用涂改液、修正带、刮纸刀。 一、选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.下列直线与一次函数![]() 的图像平行的直线是( )A.
的图像平行的直线是( )A.![]() ; B.
; B.![]() ; C.
; C.![]() ; D.
; D.![]() .2.一组数据:﹣3,1,2,6,6,8,16,99,这组数据的中位数和众数分别是( )A.6和6 B.8和6 C.6和8 D.8和163.如图,点E是菱形ABCD对角线BD上任一点,点F是CD上任一点,连接CE,EF,当
.2.一组数据:﹣3,1,2,6,6,8,16,99,这组数据的中位数和众数分别是( )A.6和6 B.8和6 C.6和8 D.8和163.如图,点E是菱形ABCD对角线BD上任一点,点F是CD上任一点,连接CE,EF,当![]() ,
,![]() 时,
时,![]() 的最小值是( )
的最小值是( )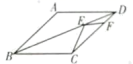 A.
A.![]() B.10 C.
B.10 C.![]() D.54.如图,在
D.54.如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 分别是
分别是![]() 和
和![]() 的中点,则
的中点,则![]() ( )
( )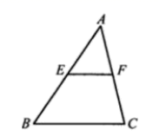 A.
A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 5.下列分解因式,正确的是( )A.
5.下列分解因式,正确的是( )A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 6.下列电视台的台标,是中心对称图形的是( )A.
6.下列电视台的台标,是中心对称图形的是( )A. B.
B. C.
C. D.
D. 7.某医药研究所开发了一种新药,在试验效果时发现,如果成人按规定剂量服用,服药后血液中的含药量逐渐增多,一段时间后达到最大值,接着药量逐步衰减直至血液中含药量为0,每毫升血液中含药量
7.某医药研究所开发了一种新药,在试验效果时发现,如果成人按规定剂量服用,服药后血液中的含药量逐渐增多,一段时间后达到最大值,接着药量逐步衰减直至血液中含药量为0,每毫升血液中含药量![]() (微克)随时间
(微克)随时间![]() (小时)的变化如图所示,下列说法:(1)2小时血液中含药量最高,达每毫升6微克.(2)每毫升血液中含药量不低于4微克的时间持续达到了6小时.(3)如果一病人下午6:00按规定剂量服此药,那么,第二天中午12:00,血液中不再含有该药,其中正确说法的个数是()
(小时)的变化如图所示,下列说法:(1)2小时血液中含药量最高,达每毫升6微克.(2)每毫升血液中含药量不低于4微克的时间持续达到了6小时.(3)如果一病人下午6:00按规定剂量服此药,那么,第二天中午12:00,血液中不再含有该药,其中正确说法的个数是()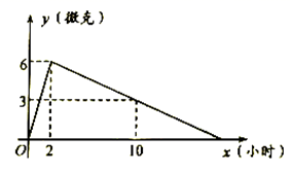 A.0 B.1C.2 D.38.已知一元二次方程
A.0 B.1C.2 D.38.已知一元二次方程![]() 有一个根为2,则另一根为A.2 B.3 C.4 D.89.关于
有一个根为2,则另一根为A.2 B.3 C.4 D.89.关于![]() 的一次函数
的一次函数![]() 的图象可能正确的是( )A.
的图象可能正确的是( )A. B.
B.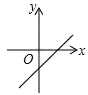 C.
C.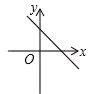 D.
D.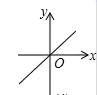 10.为迎接中考体育加试,小刚和小亮分别统计了自己最近10次跳绳比赛,下列统计量中能用来比较两人成绩稳定程度的是 ( )A.平均数 B.中位数 C.众数 D.方差11.用配方法解方程
10.为迎接中考体育加试,小刚和小亮分别统计了自己最近10次跳绳比赛,下列统计量中能用来比较两人成绩稳定程度的是 ( )A.平均数 B.中位数 C.众数 D.方差11.用配方法解方程![]() ,则方程可变形为
,则方程可变形为![]()
![]() A.
A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 12.下列事件中,必然事件是( )A.“奉贤人都爱吃鼎丰腐乳”B.“2018年上海中考,小明数学考试成绩是满分150分”C.“10只鸟关在3个笼子里,至少有一只笼子关的鸟超过3只”D.“在一副扑克牌中任意抽10张牌,其中有5张A”二、填空题(每题4分,满分20分,将答案填在答题纸上)13.解关于x的方程
12.下列事件中,必然事件是( )A.“奉贤人都爱吃鼎丰腐乳”B.“2018年上海中考,小明数学考试成绩是满分150分”C.“10只鸟关在3个笼子里,至少有一只笼子关的鸟超过3只”D.“在一副扑克牌中任意抽10张牌,其中有5张A”二、填空题(每题4分,满分20分,将答案填在答题纸上)13.解关于x的方程![]() 产生增根,则常数m的值等于________.14.在参加“森林重庆”的植树活动中,某班六个绿化小组植树的棵数分别是:10,1,1,10,11,1.则这组数据的众数是____________.15.如图,在平面直角坐标系中,已知OA=4,则点A的坐标为____________,直线OA的解析式为______________.
产生增根,则常数m的值等于________.14.在参加“森林重庆”的植树活动中,某班六个绿化小组植树的棵数分别是:10,1,1,10,11,1.则这组数据的众数是____________.15.如图,在平面直角坐标系中,已知OA=4,则点A的坐标为____________,直线OA的解析式为______________.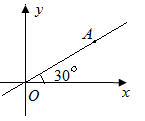 16.如图,在平行四边形ABCD中,对角线AC⊥BD,AC=10,BD=24 ,则AD=____________
16.如图,在平行四边形ABCD中,对角线AC⊥BD,AC=10,BD=24 ,则AD=____________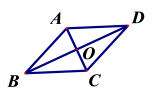 17.在平面直角坐标系中,点P(-3,2)关于x轴对称的点P1的坐标是______________.三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)18.(5分)当
17.在平面直角坐标系中,点P(-3,2)关于x轴对称的点P1的坐标是______________.三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)18.(5分)当![]() 在什么范围内取值时,关于
在什么范围内取值时,关于![]() 的一元一次方程
的一元一次方程![]() 的解满足
的解满足![]() ? 19.(5分)定义:只有一组对角是直角的四边形叫做损矩形,连结它的两个非直角顶点的线段叫做这个损矩形的直径。(1)如图1,损矩形ABCD,∠ABC=∠ADC=90°,则该损矩形的直径是线段AC,同时我们还发现损矩形中有公共边的两个三角形角的特点,在公共边的同侧的两个角是相等的。如图1中:△ABC和△ABD有公共边AB,在AB同侧有∠ADB和∠ACB,此时∠ADB=∠ACB;再比如△ABC和△BCD有公共边BC,在CB同侧有∠BAC和∠BDC,此时∠BAC=∠BDC。请再找一对这样的角来 = (2)如图2,△ABC中,∠ABC=90°,以AC为一边向形外作菱形ACEF,D为菱形ACEF的中心,连结BD,当BD平分∠ABC时,判断四边形ACEF为何种特殊的四边形?请说明理由。(3)在第(2)题的条件下,若此时AB=
? 19.(5分)定义:只有一组对角是直角的四边形叫做损矩形,连结它的两个非直角顶点的线段叫做这个损矩形的直径。(1)如图1,损矩形ABCD,∠ABC=∠ADC=90°,则该损矩形的直径是线段AC,同时我们还发现损矩形中有公共边的两个三角形角的特点,在公共边的同侧的两个角是相等的。如图1中:△ABC和△ABD有公共边AB,在AB同侧有∠ADB和∠ACB,此时∠ADB=∠ACB;再比如△ABC和△BCD有公共边BC,在CB同侧有∠BAC和∠BDC,此时∠BAC=∠BDC。请再找一对这样的角来 = (2)如图2,△ABC中,∠ABC=90°,以AC为一边向形外作菱形ACEF,D为菱形ACEF的中心,连结BD,当BD平分∠ABC时,判断四边形ACEF为何种特殊的四边形?请说明理由。(3)在第(2)题的条件下,若此时AB=![]() ,BD=
,BD=![]() ,求BC的长。
,求BC的长。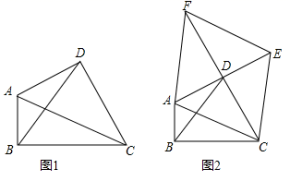 20.(8分)已知直线y1=2x与直线y2=﹣2x+4相交于点A.以下结论:①点A的坐标为A(1,2);②当x=1时,两个函数值相等:③当x<1时,y1<y2; ④直线y1=2x与直线y2=﹣2x+4在平面直角坐标系中的位置关系是平行.其中正确的个数有( )个.A.4 B.3 C.2 D.1 21.(10分)定义:我们把对角线相等的四边形叫做和美四边形.(1)请举出一种你所学过的特殊四边形中是和美四边形的例子.(2)如图1,E,F,G,H分别是四边形ABCD的边AB,BC,CD,DA的中点,已知四边形EFGH是菱形,求证:四边形ABCD是和美四边形;(3)如图2,四边形ABCD是和美四边形,对角线AC,BD相交于O,∠AOB=60°,E、F分别是AD、BC的中点,请探索EF与AC之间的数量关系,并证明你的结论.
20.(8分)已知直线y1=2x与直线y2=﹣2x+4相交于点A.以下结论:①点A的坐标为A(1,2);②当x=1时,两个函数值相等:③当x<1时,y1<y2; ④直线y1=2x与直线y2=﹣2x+4在平面直角坐标系中的位置关系是平行.其中正确的个数有( )个.A.4 B.3 C.2 D.1 21.(10分)定义:我们把对角线相等的四边形叫做和美四边形.(1)请举出一种你所学过的特殊四边形中是和美四边形的例子.(2)如图1,E,F,G,H分别是四边形ABCD的边AB,BC,CD,DA的中点,已知四边形EFGH是菱形,求证:四边形ABCD是和美四边形;(3)如图2,四边形ABCD是和美四边形,对角线AC,BD相交于O,∠AOB=60°,E、F分别是AD、BC的中点,请探索EF与AC之间的数量关系,并证明你的结论.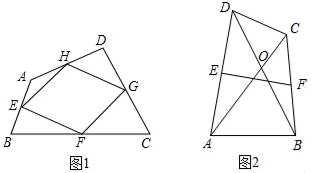 22.(10分)如图,在矩形ABCD中,E是AB的中点,连接DE、CE.(1)求证:△ADE≌△BCE;(2)若AB=6,AD=4,求△CDE的周长.
22.(10分)如图,在矩形ABCD中,E是AB的中点,连接DE、CE.(1)求证:△ADE≌△BCE;(2)若AB=6,AD=4,求△CDE的周长.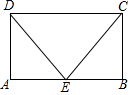 23.(12分)某工厂制作甲、乙两种窗户边框,已知同样用12米材料制成甲种边框的个数比制成乙种边框的个数少1个,且制成一个甲种边框比制成一个乙种边框需要多用
23.(12分)某工厂制作甲、乙两种窗户边框,已知同样用12米材料制成甲种边框的个数比制成乙种边框的个数少1个,且制成一个甲种边框比制成一个乙种边框需要多用![]() 的材料.(1)求制作每个甲种边框、乙种边框各用多少米材料?(2)如果制作甲、乙两种边框的材料共640米,要求制作乙种边框的数量不少于甲种边框数量的2倍,求应最多安排制作甲种边框多少个(不计材料损耗)? 参考答案 一、选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.1、B2、A3、C4、A5、B6、D7、D8、C9、C10、D11、C12、C 二、填空题(每题4分,满分20分,将答案填在答题纸上)13、
的材料.(1)求制作每个甲种边框、乙种边框各用多少米材料?(2)如果制作甲、乙两种边框的材料共640米,要求制作乙种边框的数量不少于甲种边框数量的2倍,求应最多安排制作甲种边框多少个(不计材料损耗)? 参考答案 一、选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.1、B2、A3、C4、A5、B6、D7、D8、C9、C10、D11、C12、C 二、填空题(每题4分,满分20分,将答案填在答题纸上)13、![]() 14、115、 (2
14、115、 (2![]() ,2), y=
,2), y=![]() 16、1317、(-3,-2) 三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)18、
16、1317、(-3,-2) 三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)18、![]() 19、(1)∠ABD=∠ACD;(2)四边形ACEF为正方形,理由见解析;(3)5.20、B21、(1)矩形;(2)证明见解析;(3)
19、(1)∠ABD=∠ACD;(2)四边形ACEF为正方形,理由见解析;(3)5.20、B21、(1)矩形;(2)证明见解析;(3)![]() ,证明见解析.22、(1)证明见解析;(2)1.23、(1)甲框每个2.4米,乙框每个2米;(2)最多可购买甲种边框100个.
,证明见解析.22、(1)证明见解析;(2)1.23、(1)甲框每个2.4米,乙框每个2米;(2)最多可购买甲种边框100个.
相关试卷
这是一份四川省达州市达川区2023-2024学年八上数学期末统考模拟试题含答案,共8页。试卷主要包含了考生要认真填写考场号和座位序号,化简,其结果是,的相反数是,如图,已知,计算的结果是,如图,能说明的公式是等内容,欢迎下载使用。
这是一份四川省达州市达川区2023-2024学年八上数学期末检测模拟试题含答案,共8页。试卷主要包含了如图,线段关于轴对称的线段是,下图中为轴对称图形的是,下列图形中是轴对称图形的有等内容,欢迎下载使用。
这是一份2022-2023学年四川省达州市达川区数学七年级第二学期期末联考试题含答案,共7页。









