四川省蓬安县2022-2023学年数学七下期末质量跟踪监视模拟试题含答案

四川省蓬安县2022-2023学年数学七下期末质量跟踪监视模拟试题

（时间：120分钟             分数：120分）

学校_______            年级_______        姓名_______

注意事项:

1．答题前，考生先将自己的姓名、准考证号码填写清楚，将条形码准确粘贴在条形码区域内。

2．答题时请按要求用笔。

3．请按照题号顺序在答题卡各题目的答题区域内作答，超出答题区域书写的答案无效；在草稿纸、试卷上答题无效。

4．作图可先使用铅笔画出，确定后必须用黑色字迹的签字笔描黑。

5．保持卡面清洁，不要折暴、不要弄破、弄皱，不准使用涂改液、修正带、刮纸刀。

一、选择题(每小题3分,共30分)

1．下列说法错误的是(　　)

A．“买一张彩票中大奖”是随机事件

B．不可能事件和必然事件都是确定事件

C．“穿十条马路连遇十次红灯”是不可能事件

D．“太阳东升西落”是必然事件

2．式子在实数范围内有意义，则x的取值范围是（　　）

A．x＜1 B．x≥1 C．x≤﹣1 D．x＜﹣1

3．下列所叙述的图形中，全等的两个三角形是（    ）

A．含有45°角的两个直角三角形 B．腰相等的两个等腰三角形

C．边长相等的两个等边三角形 D．一个钝角对应相等的两个等腰三角形

4．关于一次函数，下列结论正确的是　　

A．图象经过 B．图象经过第一、二、三象限

C．y随x的增大而增大 D．图象与y轴交于点

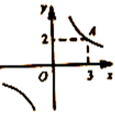
5．如图，在平面直角坐标系中，点在反比例函数的图象上.若，则自变量的取值范围是(   )

A． B． C．且 D．或

6．下列说法不正确的是（  ）

A．有两组对边分别平行的四边形是平行四边形

B．平行四边形的对角线互相平分

C．平行四边形的对边平行且相等

D．平行四边形的对角互补，邻角相等

7．据统计，湘湖景区跨湖桥遗址参观人数2016年为10.8万人次，2018年为16.8万人次，设该景点年参观人次的年平均增长率为x，则可列方程（     ）

A．10.8（1+x）=16.8 B．10.8（1+2x）=16.8

C．10.8（1+x）=16.8 D．10.8[（1+x）+（1+x）]=16.8

8．如图，在▱ABCD中，BE平分∠ABC，BC=6，DE=2，则▱ABCD的周长等于（　　）

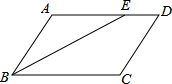
A．20 B．18 C．16 D．14

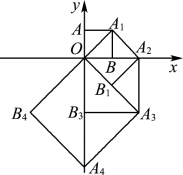
9．如图，点O（0，0），A（0，1）是正方形的两个顶点，以对角线为边作正方形，再以正方形的对角线作正方形，…，依此规律，则点的坐标是（   ）

A．（－8，0） B．（0，8）

C．（0，8） D．（0，16）

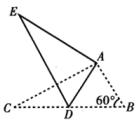
10．如图，将绕点按顺时针旋转一定角度得到，点的对应点恰好落在边上.若，，则的长为（     ）

A．1 B． C．2 D．

二、填空题(本大题共有6小题，每小题3分，共18分)

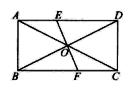
11．如图，矩形ABCD的对角线AC与BD交于点0，过点O作BD的垂线分别交AD、BC于E.F两点，若AC =2，∠DAO =300，则FB的长度为________ ．

12．已知直角坐标系内有四个点A(-1，2)，B(3，0)，C(1，4)，D(x，y)，若以A，B，C，D为顶点的四边形是平行四边形，则D点的坐标为___________________．

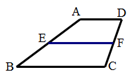
13．如图，在四边形ABCD中，AD//BC，E、F分别是AB、CD的中点，若AD=3，BC=5，则EF=____________．

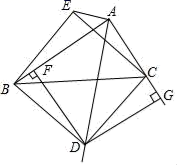
14．如图，含45°角的直角三角板DBC的直角顶点D在∠BAC的角平分线AD上，DF⊥AB于F，DG⊥AC于G，将△DBC沿BC翻转，D的对应点落在E点处，当∠BAC＝90°，AB＝4，AC＝3时，△ACE的面积等于_____．

15．观察分析下列数据：，则第17个数据是 _______ .

16．某中学规定：学生的学期体育综合成绩满分为100分，其中，期中考试成绩占40%，期末考试成绩占60%，小海这个学期的期中、期末成绩（百分制）分别是80分、90分，则小海这个学期的体育综合成绩是　 　分．

三、解下列各题(本大题共8小题，共72分)

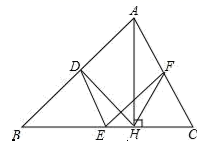
17．（8分）如图，在△ABC中，点D、E、F分别是边AB、BC、CA的中点，AH是边BC上的高．

（1）求证：四边形ADEF是平行四边形；

（2）若∠AHF＝20°，∠AHD＝50°，求∠DEF的度数．

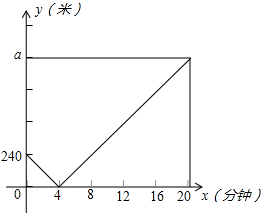
18．（8分）周末，小明、小刚两人同时各自从家沿直线匀速步行到科技馆参加科技创新活动，小明家、小刚家、科技馆在一条直线上．已知小明到达科技馆花了20分钟．设两人出发（分钟）后，小明离小刚家的距离为（米），与的函数关系如图所示．

（1）小明的速度为        米/分，       ，小明家离科技馆的距离为     米；

（2）已知小刚的步行速度是40米/分，设小刚步行时与家的距离为（米），请求出与之间的函数关系式，并在图中画出 （米）与 （分钟）之间的函数关系图象；

（3）小刚出发几分钟后两人在途中相遇？

19．（8分）阅读下列材料解决问题

两个多位数整数，若它们各数位上的数字之和相等，则称这两个多位数互为“调和数”，例如37和82，它们各数位上的数字之和分别为3+7和8+2，显然3+7＝8+2＝10故37和82互为“调和数”．

（1）下列说法错误的是    

A．123和51互为调和数”       B．345和513互为“调和数

C．2018和8120互为“调和数”  D．两位数和互为“调和数”

（2）若A、B是两个不等的两位数，A＝，B＝，A和B互为“调和数”，且A与B之和是B与A之差的3倍，求满足条件的两位数A．

20．（8分）如图，已知边长为6的菱形ABCD中，∠ABC＝60°，点E，F分别为AB，AD边上的动点，满足，连接EF交AC于点G，CE、CF分别交BD于点M，N，给出下列结论：①△CEF是等边三角形；②∠DFC＝∠EGC；    ③若BE＝3，则BM＝MN＝DN；④；    ⑤△ECF面积的最小值为．其中所有正确结论的序号是______

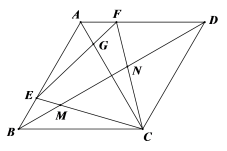
21．（8分）四边形ABCD是正方形，AC与BD，相交于点O，点E、F是直线AD上两动点，且AE=DF，CF所在直线与对角线BD所在直线交于点G，连接AG，直线AG交BE于点H．

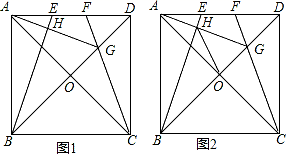
（1）如图1，当点E、F在线段AD上时，求证：∠DAG=∠DCG；

（2）如图1，猜想AG与BE的位置关系，并加以证明；

（3）如图2，在（2）条件下，连接HO，试说明HO平分∠BHG．

22．（10分）（知识链接）连结三角形两边中点的线段，叫做三角形的中位线．

（动手操作）小明同学在探究证明中位线性质定理时，是沿着中位线将三角形剪开然后将它们无缝隙、无重叠的拼在一起构成平行四边形，从而得出：三角形中位线平行于第三边且等于第三边的一半．

（性质证明）小明为证明定理，他想利用三角形全等、平行四边形的性质来证明．请你帮他完成解题过程(要求：画出图形，根据图形写出已知、求证和证明过程)．

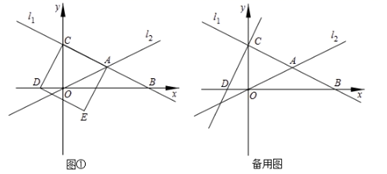
23．（10分）如图①，在平面直角坐标系中，直线：分别与轴、轴交于点、，且与直线：交于点，以线段为边在直线的下方作正方形，此时点恰好落在轴上．

（1）求出三点的坐标．

（2）求直线的函数表达式．

（3）在（2）的条件下，点是射线上的一个动点，在平面内是否存在点，使得以、、、为顶点的四边形是菱形？若存在，直接写出点的坐标；若不存在，请说明理由．

24．（12分）已知：如图，菱形ABCD的对角线AC，BD相交于O，点E，F分别是AD，DC的中点，已知OE=，EF=3，求菱形ABCD的周长和面积．

参考答案

一、选择题(每小题3分,共30分)

1、C

2、B

3、C

4、D

5、D

6、D

7、C

8、A

9、D

10、C

二、填空题(本大题共有6小题，每小题3分，共18分)

11、2

12、 (5，2)，(-3，6)，(1，-2) ．

13、1

14、

15、

16、1

三、解下列各题(本大题共8小题，共72分)

17、（1）见解析；（2）70°.

18、（1）60；960；1200；（2）＝40（0≤≤24）；见解析；（3）12分钟．

19、（1）B（2）18

20、①②③⑤

21、（1）证明见解析（2）AG⊥BE（3）证明见解析

22、见解析

23、（1），，；（2）；（3）存在，，，．

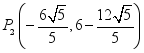24、20，1