


天津和平区天津市双菱中学2022-2023学年数学七下期末经典试题含答案
展开
这是一份天津和平区天津市双菱中学2022-2023学年数学七下期末经典试题含答案,共7页。试卷主要包含了正方形面积为,则对角线的长为,一次函数与图象如图,下列分式是最简分式的是等内容,欢迎下载使用。
天津和平区天津市双菱中学2022-2023学年数学七下期末经典试题(时间:120分钟 分数:120分) 学校_______ 年级_______ 姓名_______ 注意事项:1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其它答案标号。回答非选择题时,将答案写在答题卡上,写在本试卷上无效。3.考试结束后,将本试卷和答题卡一并交回。 一、选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.若点A(x1,y1)、B(x2,y2)、C(x3,y3)都在反比例函数![]() 的图象上,并且x1<0<x2<x3,则下列各式中正确的是( )A.y1<y2<y3 B.y2<y3<y1 C.y1<y3<y2 D.y3<y1<y22.如图,将平行四边形ABCD绕点A逆时针旋转40°,得到平行四边形AB′C′D′,若点B′恰好落在BC边上,则∠DC′B′的度数为( )
的图象上,并且x1<0<x2<x3,则下列各式中正确的是( )A.y1<y2<y3 B.y2<y3<y1 C.y1<y3<y2 D.y3<y1<y22.如图,将平行四边形ABCD绕点A逆时针旋转40°,得到平行四边形AB′C′D′,若点B′恰好落在BC边上,则∠DC′B′的度数为( )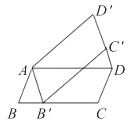 A.60° B.65° C.70° D.75°3.平行四边形具有的特征是( )A.四个角都是直角 B.对角线相等C.对角线互相平分 D.四边相等4.下列多项式中,不能运用公式进行分解因式的是( )A.a2+b2 B.x2﹣9 C.m2﹣n2 D.x2+2xy+y25.如图,点
A.60° B.65° C.70° D.75°3.平行四边形具有的特征是( )A.四个角都是直角 B.对角线相等C.对角线互相平分 D.四边相等4.下列多项式中,不能运用公式进行分解因式的是( )A.a2+b2 B.x2﹣9 C.m2﹣n2 D.x2+2xy+y25.如图,点![]() 是边长为2的菱形
是边长为2的菱形![]() 对角线
对角线![]() 上的一个动点,点
上的一个动点,点![]() ,
,![]() 分别是
分别是![]() ,
,![]() 边上的中点,则
边上的中点,则![]() 的最小值是( )
的最小值是( )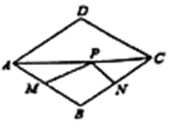 A.1 B.2 C.
A.1 B.2 C.![]() D.46.观察下列图形,既是轴对称图形又是中心对称图形的有
D.46.观察下列图形,既是轴对称图形又是中心对称图形的有 A.1个 B.2个 C.3个 D.4个7.小明为画一个零件的轴截面,以该轴截面底边所在的直线为x轴,对称轴为y轴,建立如图所示的平面直角坐标系.若坐标轴的单位长度取1mm,则图中转折点
A.1个 B.2个 C.3个 D.4个7.小明为画一个零件的轴截面,以该轴截面底边所在的直线为x轴,对称轴为y轴,建立如图所示的平面直角坐标系.若坐标轴的单位长度取1mm,则图中转折点![]() 的坐标表示正确的是
的坐标表示正确的是![]()
![]()
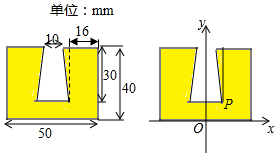 A.(5,30) B.(8,10) C.(9,10) D.(10,10)8.正方形面积为
A.(5,30) B.(8,10) C.(9,10) D.(10,10)8.正方形面积为![]() ,则对角线的长为( )A.6 B.
,则对角线的长为( )A.6 B.![]() C.9 D.
C.9 D.![]() 9.一次函数
9.一次函数![]() 与
与![]() 图象如图:则下列结论①k<0;②a>0;③不等式x+a<kx+b的解集是x<3;④a−b=3k−3中,正确的个数是( )
图象如图:则下列结论①k<0;②a>0;③不等式x+a<kx+b的解集是x<3;④a−b=3k−3中,正确的个数是( ) 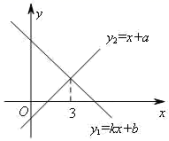 A.1个 B.2个 C.3个 D.4个10.下列分式是最简分式的是( )A.
A.1个 B.2个 C.3个 D.4个10.下列分式是最简分式的是( )A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 11.若不等式组
11.若不等式组![]() 恰有两个整数解,则a的取值范围是( )A.-1≤a<0 B.-1<a≤0 C.-1≤a≤0 D.-1<a<012.如图,在矩形ABCD中(AD>AB),点E是BC上一点,且DE=DA,AF⊥DE,垂足为点F,在下列结论中,不一定正确的是( )
恰有两个整数解,则a的取值范围是( )A.-1≤a<0 B.-1<a≤0 C.-1≤a≤0 D.-1<a<012.如图,在矩形ABCD中(AD>AB),点E是BC上一点,且DE=DA,AF⊥DE,垂足为点F,在下列结论中,不一定正确的是( )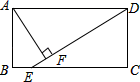 A.△AFD≌△DCE B.AF=
A.△AFD≌△DCE B.AF=![]() ADC.AB=AF D.BE=AD﹣DF二、填空题(每题4分,满分20分,将答案填在答题纸上)13.
ADC.AB=AF D.BE=AD﹣DF二、填空题(每题4分,满分20分,将答案填在答题纸上)13.![]() 的非负整数解为______.14.如图,在平面直角坐标系中,一次函数
的非负整数解为______.14.如图,在平面直角坐标系中,一次函数![]() 和函数
和函数![]() 的图象交于A、B两点.利用函数图象直接写出不等式
的图象交于A、B两点.利用函数图象直接写出不等式![]() 的解集是____________.
的解集是____________.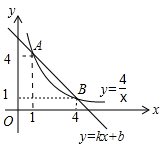 15.如图,菱形ABCD的周长为16cm,BC的垂直平分线EF经过点A,则对角线BD长为_____________cm.
15.如图,菱形ABCD的周长为16cm,BC的垂直平分线EF经过点A,则对角线BD长为_____________cm.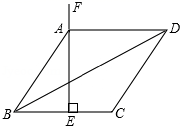 16.菱形
16.菱形![]() 的两条对角线相交于
的两条对角线相交于![]() ,若
,若![]() ,
,![]() ,则菱形
,则菱形![]() 的周长是___.17.命题“若
的周长是___.17.命题“若![]() ,则
,则![]() .”的逆命题是_____命题.(填“真”或“假”)三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)18.(5分)如图,△ABC中,AB=10,BC=6,AC=8.(1)求证:△ABC是直角三角形;(2)若D是AC的中点,求BD的长.(结果保留根号)
.”的逆命题是_____命题.(填“真”或“假”)三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)18.(5分)如图,△ABC中,AB=10,BC=6,AC=8.(1)求证:△ABC是直角三角形;(2)若D是AC的中点,求BD的长.(结果保留根号)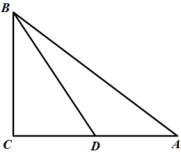 19.(5分)下面是小明化简
19.(5分)下面是小明化简![]() 的过程解:
的过程解:![]() =
=![]() ①=
①=![]() ②=﹣
②=﹣![]() ③(1)小明的解答是否正确?如有错误,错在第几步?(2)求当x=
③(1)小明的解答是否正确?如有错误,错在第几步?(2)求当x=![]() 时原代数式的值. 20.(8分)如图,直线l1:y1=−
时原代数式的值. 20.(8分)如图,直线l1:y1=−![]() x+m与y轴交于点A(0,6),直线l2:y2=kx+1分别与x轴交于点B(-2,0),与y轴交于点C.两条直线相交于点D,连接AB.(1)求两直线交点D的坐标;(2)求△ABD的面积;
x+m与y轴交于点A(0,6),直线l2:y2=kx+1分别与x轴交于点B(-2,0),与y轴交于点C.两条直线相交于点D,连接AB.(1)求两直线交点D的坐标;(2)求△ABD的面积;
(3)根据图象直接写出y1>y2时自变量x的取值范围.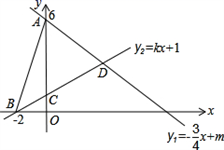 21.(10分)如图,抛物线y=x2+bx+c与x轴交于A(﹣1,0),B(3,0)两点,与
21.(10分)如图,抛物线y=x2+bx+c与x轴交于A(﹣1,0),B(3,0)两点,与![]() 轴交于
轴交于![]() 点.(1)求该抛物线的解析式;(2)P是y轴正半轴上一点,且△PAB是以AB为腰的等腰三角形,试求点P的坐标;(3)作直线BC,若点Q是直线BC下方抛物线上的一动点,三角形QBC面积是否有最大值,若有,请求出此时Q点的坐标;若没有,请说明理由.
点.(1)求该抛物线的解析式;(2)P是y轴正半轴上一点,且△PAB是以AB为腰的等腰三角形,试求点P的坐标;(3)作直线BC,若点Q是直线BC下方抛物线上的一动点,三角形QBC面积是否有最大值,若有,请求出此时Q点的坐标;若没有,请说明理由.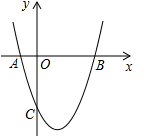 22.(10分)如图,直线
22.(10分)如图,直线![]() 分别与
分别与![]() 轴、
轴、![]() 轴交于点
轴交于点![]() ,
,![]() ;直线
;直线![]() 分别与
分别与![]() 轴交于点
轴交于点![]() ,与直线
,与直线![]() 交于点
交于点![]() ,已知关于
,已知关于![]() 的不等式
的不等式![]() 的解集是
的解集是![]() .
.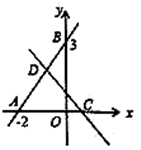 (1)分别求出
(1)分别求出![]() ,
,![]() ,
,![]() 的值;(2)求
的值;(2)求![]() . 23.(12分)在平面直角坐标系中,四边形OBCD是正方形,且D(0,2),点E是线段OB延长线上一点,M是线段OB上一动点(不包括点O、B),作MN⊥DM,垂足为M,交∠CBE的平分线于点N.(1)写出点C的坐标;(2)求证:MD=MN;(3)连接DN交BC于点F,连接FM,下列两个结论:①FM的长度不变;②MN平分∠FMB,其中只有一个结论是正确的,请你指出正确的结论,并给出证明
. 23.(12分)在平面直角坐标系中,四边形OBCD是正方形,且D(0,2),点E是线段OB延长线上一点,M是线段OB上一动点(不包括点O、B),作MN⊥DM,垂足为M,交∠CBE的平分线于点N.(1)写出点C的坐标;(2)求证:MD=MN;(3)连接DN交BC于点F,连接FM,下列两个结论:①FM的长度不变;②MN平分∠FMB,其中只有一个结论是正确的,请你指出正确的结论,并给出证明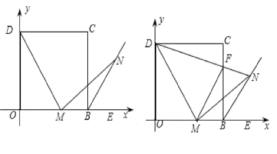 参考答案 一、选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.1、B2、C3、C4、A5、B6、C7、C8、B9、C10、C11、A12、B 二、填空题(每题4分,满分20分,将答案填在答题纸上)13、0,1,214、
参考答案 一、选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.1、B2、C3、C4、A5、B6、C7、C8、B9、C10、C11、A12、B 二、填空题(每题4分,满分20分,将答案填在答题纸上)13、0,1,214、![]() 15、4
15、4![]() .16、
.16、![]() 17、假 三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)18、 (1)见解析;(2)2
17、假 三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)18、 (1)见解析;(2)2![]() .19、(1)第①步(2)
.19、(1)第①步(2)![]() 20、(1)D点坐标为(4,3)(1)15;(3)x<421、(1)y=x2-2x-2;(2)P点的坐标为( 0,
20、(1)D点坐标为(4,3)(1)15;(3)x<421、(1)y=x2-2x-2;(2)P点的坐标为( 0,![]() )或( 0,
)或( 0,![]() );(2)点Q(
);(2)点Q(![]() , -
, - ![]() ).22、(1)
).22、(1)![]() ,
,![]() ,
,![]() ;(2)
;(2)![]() 23、(1)点
23、(1)点![]() 的坐标为
的坐标为![]() ;(2)见解析;(3)MN平分∠FMB成立,证明见解析
;(2)见解析;(3)MN平分∠FMB成立,证明见解析
相关试卷
这是一份2023-2024学年天津和平区天津市双菱中学八上数学期末检测试题含答案,共6页。
这是一份天津市和平区双菱中学2023-2024学年数学八上期末联考模拟试题含答案,共8页。试卷主要包含了答题时请按要求用笔,如果,那么的值为,下列运算正确的是等内容,欢迎下载使用。
这是一份天津市和平区双菱中学2023-2024学年八上数学期末检测试题含答案,共7页。试卷主要包含了考生要认真填写考场号和座位序号,下列各式中,正确的是,数据5,7,8,8,9的众数是,若分式的值不存在,则的值是等内容,欢迎下载使用。










