


天津市2022-2023学年数学七下期末质量检测试题含答案
展开天津市2022-2023学年数学七下期末质量检测试题
(时间:120分钟 分数:120分)
学校_______ 年级_______ 姓名_______
注意事项
1.考生要认真填写考场号和座位序号。
2.试题所有答案必须填涂或书写在答题卡上,在试卷上作答无效。第一部分必须用2B 铅笔作答;第二部分必须用黑色字迹的签字笔作答。
3.考试结束后,考生须将试卷和答题卡放在桌面上,待监考员收回。
一、选择题(每小题3分,共30分)
1.甲、乙二人做某种机械零件,已知甲每小时比乙少做6个,甲做60个所用时间与乙做90个所用时间相等,求甲、乙每小时各做零件多少个.如果设甲每小时做x个,那么所列方程是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
2.下列各数中比3大比4小的无理数是( )
A.![]() B.
B.![]() C.3.1 D.
C.3.1 D.![]()
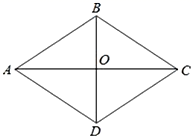
3.如图,在菱形![]() 中,对角线
中,对角线![]() 、
、![]() 相交于点
相交于点![]() ,下列结论中不一定成立的是( )
,下列结论中不一定成立的是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
4.已知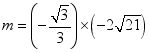 ,则( )
,则( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
5.在四边形![]() 中,若
中,若![]() ,则
,则![]() 等于( )
等于( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
6.在平面直角坐标系中,若一图形各点的纵坐标不变,横坐标分别减5,则图形与原图形相比( )
A.向右平移了5个单位长度 B.向左平移了5个单位长度
C.向上平移了5个单位长度 D.向下平移了5个单位长度
7.在四边形![]() 中,给出下列条件:①
中,给出下列条件:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ,选其中两个条件不能判断四边形
,选其中两个条件不能判断四边形![]() 是平行四边形的是
是平行四边形的是![]()
![]()
A.①② B.①③ C.①④ D.②④
8.一次函数y=kx﹣b,当k<0,b<0时的图象大致位置是( )
A.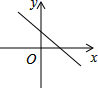 B.
B.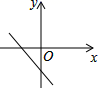 C.
C. D.
D.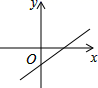
9.下列命题中,是假命题的是( )
A.在△ABC中,若∠A:∠B:∠C=1:2:3,则△ABC是直角三角形
B.在△ABC中,若a2=(b+c) (b-c),则△ABC是直角三角形
C.在△ABC中,若∠B=∠C=∠A,则△ABC是直角三角形
D.在△ABC中,若a:b:c=5:4:3,则△ABC是直角三角形
10.下列交通标志是轴对称图形的是( )
A. B.
B. C.
C. D.
D.
二、填空题(本大题共有6小题,每小题3分,共18分)
11.写出一个经过二、四象限的正比例函数_________________________.
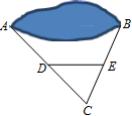
12.在湖的两侧有A,B两个观湖亭,为测定它们之间的距离,小明在岸上任选一点C,并量取了AC中点D和BC中点E之间的距离为50米,则A,B之间的距离应为______米.
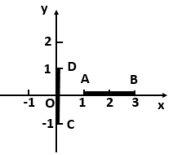
13.如图,已知![]() ,
,![]() ,
,![]() ,
,![]() ,若线段
,若线段![]() 可由线段
可由线段![]() 围绕旋转中心
围绕旋转中心![]() 旋转而得,则旋转中心
旋转而得,则旋转中心![]() 的坐标是______.
的坐标是______.
14.若![]() =
=![]() .则
.则![]() =_____.
=_____.
15.一次函数y=kx+3的图象不经过第3象限,那么k的取值范围是______
16.函数y=﹣6x+5的图象是由直线y=﹣6x向_____平移_____个单位长度得到的.
三、解下列各题(本大题共8小题,共72分)
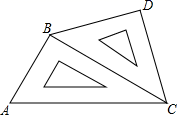
17.(8分)小明将一副三角板如图所示摆放在一起,发现只要知道其中一边的长就可以求出其他各边的长.若已知CD=![]() ,求AB的长.
,求AB的长.
18.(8分)解方程:(1)2x 2+4x+2=0; (2)![]() x 2 x 4 0
x 2 x 4 0
19.(8分)计算:
(1)![]() ; (2)
; (2)![]() .
.
20.(8分)列分式方程解应用题:今年植树节,某校师生到距学校20千米的公路旁植树,一班师生骑自行车先走,走了16千米后,二班师生乘汽车出发,结果同时到达.已知汽车的速度比自行车的速度每小时快60千米,求两种车的速度各是多少?
21.(8分)若变量z是变量y的函数,同时变量y是变量x的函数,那么我们把变量z叫做变量x的“迭代函数”.
例如:z2y3,yx1,则z2x132x1,那么z2x1就是z与x之间的“迭代函数”解析式.
(1)当2006x2020时,zy2,![]() ,请求出z与x之间的“迭代函数”的解析式及z的最小值;
,请求出z与x之间的“迭代函数”的解析式及z的最小值;
(2)若z2ya,yax24axba0,当1x3时,“迭代函数”z的取值范围为1z17,求a和b的值;
(3)已知一次函数yax1经过点1,2,zay2b2ycb4(其中a、b、c均为常数),聪明的你们一定知道“迭代函数”z是x的二次函数,若x1、x2(x1x2)是“迭代函数”z3的两个根,点x3,2是“迭代函数”z的顶点,而且x1、x2、x3还是一个直角三角形的三条边长,请破解“迭代函数”z关于x的函数解析式.
22.(10分)某科技公司研发出一款多型号的智能手表,一家代理商出售该公司的A型智能手表,去年销售总额为8000元,今年A型智能手表的售价每只比去年降了60元,若售出的数量与去年相同,销售总额将比去年减少25%.
(1)请问今年A型智能手表每只售价多少元?
(2)今年这家代理商准备新进一批A型智能手表和B型智能手表共100只,它们的进货价与销售价格如下表,若B型智能手表进货量不超过A型智能手表数量的3倍,所进智能手表可全部售完,请你设计出进货方案,使这批智能手表获利最多,并求出最大利润是多少元?
| A型智能手表 | B型智能手表 |
进价 | 130元/只 | 150元/只 |
售价 | 今年的售价 | 230元/只 |
23.(10分) (1)已知一个正分数![]() (m>n>0),将分子、分母同时增加1,得到另一个正分数
(m>n>0),将分子、分母同时增加1,得到另一个正分数![]() ,比较
,比较![]() 和
和![]() 的值的大小,并证明你的结论;
的值的大小,并证明你的结论;
(2)若正分数![]() (m>n>0)中分子和分母同时增加k(整数k>0),则
(m>n>0)中分子和分母同时增加k(整数k>0),则![]() _____
_____![]() .
.
(3)请你用上面的结论解释下面的问题:
建筑学规定:民用住宅窗户面积必须小于地板面积,但按采光标准,窗户面积与地板面积的比应不小于10%,并且这个比值越大,住宅的采光条件越好.若原来的地板面积和窗户面积分别为x,y,同时增加相等的窗户面积和地板面积,则住宅的采光条件是变好还是变坏?请说明理由.
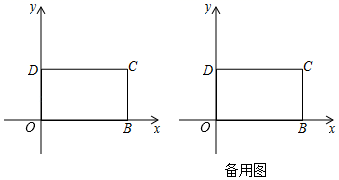
24.(12分)如图,矩形OBCD中,OB=5,OD=3,以O为原点建立平面直角坐标系,点B,点D分别在x轴,y轴上,点C在第一象限内,若平面内有一动点P,且满足S△POB=![]() S矩形OBCD,问:
S矩形OBCD,问:
(1)当点P在矩形的对角线OC上,求点P的坐标;
(2)当点P到O,B两点的距离之和PO+PB取最小值时,求点P的坐标.
参考答案
一、选择题(每小题3分,共30分)
1、A
2、A
3、D
4、B
5、B
6、B
7、A
8、A
9、C
10、C
二、填空题(本大题共有6小题,每小题3分,共18分)
11、y=-2x …(答案不唯一)
12、1
13、![]() 或
或![]()
14、1.
15、k<0
16、上 1.
三、解下列各题(本大题共8小题,共72分)
17、![]() .
.
18、(1)![]() ;(2)
;(2)![]() .
.
19、(1)6(2)9
20、汽车和自行车的速度分别是75千米/时、15千米/时.
21、(1)z= -![]() x+6;-1004;(2)
x+6;-1004;(2)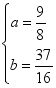 或
或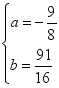 ;(3)
;(3)![]()
22、(1)180元;(2)方案为A型手表25只,B型手表75只,获利最多,最大利润是7250元.
23、 (1)![]() >
>![]() ,证明见解析;(2)>;(3)住宅的采光条件变好了
,证明见解析;(2)>;(3)住宅的采光条件变好了
24、(1)P(![]() ,2);(2)(
,2);(2)(![]() ,2)或(﹣
,2)或(﹣![]() ,2)
,2)
天津市蓟县名校2022-2023学年七下数学期末教学质量检测模拟试题含答案: 这是一份天津市蓟县名校2022-2023学年七下数学期末教学质量检测模拟试题含答案,共8页。
天津市津南区2022-2023学年数学七下期末质量跟踪监视试题含答案: 这是一份天津市津南区2022-2023学年数学七下期末质量跟踪监视试题含答案,共6页。试卷主要包含了考生要认真填写考场号和座位序号,一次函数的图象不经过象限等内容,欢迎下载使用。
天津市津南区名校2022-2023学年数学七下期末质量检测试题含答案: 这是一份天津市津南区名校2022-2023学年数学七下期末质量检测试题含答案,共6页。试卷主要包含了考生必须保证答题卡的整洁等内容,欢迎下载使用。












