


天津市河北区红光中学2022-2023学年七下数学期末质量跟踪监视模拟试题含答案
展开天津市河北区红光中学2022-2023学年七下数学期末质量跟踪监视模拟试题
(时间:120分钟 分数:120分)
学校_______ 年级_______ 姓名_______
注意事项
1.考生要认真填写考场号和座位序号。
2.试题所有答案必须填涂或书写在答题卡上,在试卷上作答无效。第一部分必须用2B 铅笔作答;第二部分必须用黑色字迹的签字笔作答。
3.考试结束后,考生须将试卷和答题卡放在桌面上,待监考员收回。
一、选择题(每小题3分,共30分)
1.如图,在平行四边形ABCD中,用直尺和圆规作的∠BAD平分线交BC于点E,若AE=8,AB=5,则BF的长为( )
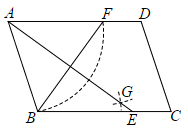
A.4 B.5 C.6 D.8
2.菱形的两条对角线长分别是6cm和8cm,则它的面积是( )
A.6cm2 B.12cm2 C.24cm2 D.48cm2
3.下列多项式能用完全平方公式进行分解因式的是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
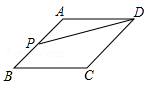
4.如图,点![]() 是菱形
是菱形![]() 边上的一动点,它从点
边上的一动点,它从点![]() 出发沿在
出发沿在![]() 路径匀速运动到点
路径匀速运动到点![]() ,设
,设![]() 的面积为
的面积为![]() ,
,![]() 点的运动时间为
点的运动时间为![]() ,则
,则![]() 关于
关于![]() 的函数图象大致为
的函数图象大致为![]()
![]()
A. B.
B.
C. D.
D.
5.如图,在正方形![]() 中,
中,![]() 为边
为边![]() 上一点,将
上一点,将![]() 沿
沿![]() 折叠至
折叠至![]() 处,
处, ![]() 与
与![]() 交于点
交于点![]() ,若
,若![]() ,则
,则![]() 的大小为( )
的大小为( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
6.下列命题中,假命题是( )
A.对角线互相平分的四边形是平行四边形
B.对角线互相平分且相等的四边形是矩形
C.对角线互相垂直平分的四边形是菱形
D.对角线互相垂直且相等的四边形是正方形
7.点![]() 在第
在第![]()
![]() 象限.
象限.
A.第一象限 B.第二象限 C.第三象限 D.第四象限
8.如图1,四边形![]() 中,
中,![]() ,
,![]() .动点
.动点![]() 从点
从点![]() 出发沿折线
出发沿折线![]() 方向以
方向以![]() 单位/秒的速度匀速运动,在整个运动过程中,
单位/秒的速度匀速运动,在整个运动过程中,![]() 的面积
的面积![]() 与运动时间
与运动时间![]() (秒)的函数图像如图2所示,则AD等于( )
(秒)的函数图像如图2所示,则AD等于( )

A.10 B.![]() C.8 D.
C.8 D.![]()
9.菱形ABCD的一条对角线长为6,边AB的长为方程y2﹣7y+10=0的一个根,则菱形ABCD的周长为( )
A.8 B.20 C.8或20 D.10
10.小明研究二次函数![]() (
(![]() 为常数)性质时有如下结论:①该二次函数图象的顶点始终在平行于x轴的直线上;②该二次函数图象的顶点与x轴的两个交点构成等腰直角三角形;③当
为常数)性质时有如下结论:①该二次函数图象的顶点始终在平行于x轴的直线上;②该二次函数图象的顶点与x轴的两个交点构成等腰直角三角形;③当![]() 时,y随x的增大而增大,则m的取值范围为
时,y随x的增大而增大,则m的取值范围为![]() ;④点
;④点![]() 与点
与点![]() 在函数图象上,若
在函数图象上,若![]() ,
,![]() ,则
,则![]() .其中正确结论的个数为( )
.其中正确结论的个数为( )
A.1 B.2 C.3 D.4
二、填空题(本大题共有6小题,每小题3分,共18分)
11.有一组数据如下:2,3,a,5,6,它们的平均数是4,则这组数据的方差是 .
12.在菱形![]() 中,
中,![]() 在菱形所在平面内,以对角线
在菱形所在平面内,以对角线![]() 为底边作顶角是
为底边作顶角是![]() 的等腰
的等腰![]() 则
则![]() _________________.
_________________.
13.使函数![]() 有意义的
有意义的![]() 的取值范围是________.
的取值范围是________.
14.当![]() _____________时,
_____________时,![]() 在实数范围内有意义.
在实数范围内有意义.
15.函数y=![]() 的自变量x的取值范围为____________.
的自变量x的取值范围为____________.
16.如图,一束光线从y轴上的点A(0,1)出发,经过x轴上的点C反射后经过点B(6,2),则光线从A点到B点经过的路线长度为 .

三、解下列各题(本大题共8小题,共72分)
17.(8分)如图,菱形ABCD对角线交于点O,BE∥AC,AE∥BD,EO与AB交于点F.

(1)试判断四边形AEBO的形状,并说明你的理由;(2)求证:EO=DC.
18.(8分)如图,在4×3的正方形网格中,每个小正方形的边长都是1.
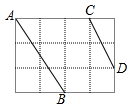
(1)分别求出线段AB,CD的长度;
(2)在图中画出线段EF,使得EF的长为![]() ,用AB、CD、EF三条线段能否构成直角三角形,请说明理由.
,用AB、CD、EF三条线段能否构成直角三角形,请说明理由.
19.(8分)计算题:
(1)解不等式组
(2)先化筒,再求值(![]() )
)![]() ,其中m=
,其中m=![]()
(3)解方程![]() =1-
=1-![]()
20.(8分)已知:如图,AM是△ABC的中线,D是线段AM的中点,AM=AC,AE∥BC.求证:四边形EBCA是等腰梯形.

21.(8分)如图,lA、lB分别表示A步行与B骑车在同一路上行驶的路程S与时间t的关系.
(1)B出发时与A相距_____千米;
(2)走了一段路后,自行车发生故障进行修理,所用的时间是____小时;
(3)B出发后_____小时与A相遇;
(4)求出A行走的路程S与时间t的函数关系式;(写出计算过程)
(5)请通过计算说明:若B的自行车不发生故障,保持出发时的速度前进,何时与A相遇.

22.(10分)某石化乙烯厂某车间生产甲、乙两种塑料的相关信息如下表,请你解答下列问题:
| 出厂价 | 成本价 | 排污处理费 |
甲种塑料 | 2100(元/吨) | 800(元/吨) | 200(元/吨) |
乙种塑料 | 2400(元/吨) | 1100(元/吨) | 100(元/吨) 另每月还需支付设备管理、维护费20000元 |
(1)设该车间每月生产甲、乙两种塑料各x吨,利润分别为y1元和y2元,分别求出y1和y2与x的函数关系式(注:利润=总收入-总支出);
(2)已知该车间每月生产甲、乙两种塑料均不超过400吨,若某月要生产甲、乙两种塑料共700吨,求该月生产甲、乙塑料各多少吨时,获得的总利润最大?最大利润是多少?
23.(10分)如图,点E,F是平行四边形ABCD对角线BD上的点,且BF=DE.求证:AE=CF.

24.(12分)关于x、y的方程组![]() 的解满足x﹣2y≥1,求满足条件的k的最大整数值.
的解满足x﹣2y≥1,求满足条件的k的最大整数值.
参考答案
一、选择题(每小题3分,共30分)
1、C
2、C
3、C
4、B
5、B
6、D
7、A
8、B
9、B
10、D
二、填空题(本大题共有6小题,每小题3分,共18分)
11、1
12、105°或45°
13、![]() 且
且![]()
14、a≥1
15、x≥-1
16、3![]()
三、解下列各题(本大题共8小题,共72分)
17、证明见解析
18、 (1)AB=![]() ,CD=
,CD=![]() ;(2)能否构成直角三角形,理由见解析.
;(2)能否构成直角三角形,理由见解析.
19、(1)-1≤x<![]() ;(2)-5;(3)x=
;(2)-5;(3)x=![]() 是原分式方程的根.
是原分式方程的根.
20、见解析.
21、(1)10;(2)1;(3)3;(4)![]() ;(5)1小时.
;(5)1小时.
22、(1)![]() 与x的函数关系式为
与x的函数关系式为![]() =1100x;
=1100x;![]() 与x的函数关系式为
与x的函数关系式为![]() =1200x-20000;(2)该月生产甲、乙两种塑料分别为300吨和2吨时总利润最大,最大总利润是790000元.
=1200x-20000;(2)该月生产甲、乙两种塑料分别为300吨和2吨时总利润最大,最大总利润是790000元.
23、证明见解析.
24、满足条件的k的最大整数值为1.
天津市河北区红光中学2023-2024学年九上数学期末达标检测模拟试题含答案: 这是一份天津市河北区红光中学2023-2024学年九上数学期末达标检测模拟试题含答案,共7页。试卷主要包含了考生必须保证答题卡的整洁,一元二次方程的正根的个数是,若反比例函数y=等内容,欢迎下载使用。
天津市河北区扶轮中学2023-2024学年九上数学期末质量跟踪监视试题含答案: 这是一份天津市河北区扶轮中学2023-2024学年九上数学期末质量跟踪监视试题含答案,共8页。试卷主要包含了按下面的程序计算,下列四种说法,一个物体如图所示,它的俯视图是等内容,欢迎下载使用。
天津市南开区翔宇中学2022-2023学年数学七下期末质量跟踪监视试题含答案: 这是一份天津市南开区翔宇中学2022-2023学年数学七下期末质量跟踪监视试题含答案,共6页。试卷主要包含了将一个n边形变成边形,内角和将等内容,欢迎下载使用。












