初中数学第二十四章 相似三角形第二节 比例线段24.2 比例线段一等奖教学设计

这是一份初中数学第二十四章 相似三角形第二节 比例线段24.2 比例线段一等奖教学设计，共9页。教案主要包含了温故知新，问题引入，探索新知，获得感悟，例题选讲，训练提高，课堂小结，加深理解，回家作业，复习巩固等内容，欢迎下载使用。
课题：24.2  比例线段（1）—比例线段及其相关性质教材分析：由于图形的相似与比例线段密不可分，因此在形成相似形的概念之后，安排学习比例线段，为研究相似三角形提供了必要的知识准备。本课主要由两部分组成，第一部分是有关线段比例的基本概念和性质及相关的计算；第二部分是比例的拓展性质。教学目标：1、知道两条线段比的意义；2、理解比例线段及其有关概念；3、知道比例线段的性质，能运用比例线段的性质对进行简单的变形。教学重点：引进两条线段的比和比例线段；导出比例线段的性质并进行初步的运用。教学难点：合比、等比性质的综合运用。教学过程：一、温故知新，问题引入复习：1、两个数与相除叫做两个数的比，记作，若的比值为k，则；2、如果，那么就说a,b,c,d成比例，这个比例式可变形为等积式，还可变形为比例式；3、若，则称b为a与c的比例中项。我们已经知道图形的相似与线段的长度的比及比例有密切关联，为了研究相似，需要先研究比例线段。练习1：已知：AB=50cm，BC=2.5dm，A’B’=0.2m，B’C’=10cm。          求：。解：。【说明】学生在六年级已经学过比、比例及比例的基本性质。通过回顾比和比例的概念，给出了两条线段的比和比例线段的概念。比例线段是有特定含义的一种比例，学生在以前学过的有关比例的性质，也是比例线段的性质，可让学生列出比例线段的基本性质。问题1：通过练习1，我们发现线段AB、BC、A’B’、B’C’之间有怎样的关系？分析：我们可以说线段AB、BC、A’B’、B’C’成比例，也可以称它们为比例线段。板书：24.2  比例线段（1）    1、两条线段长度的比叫做两条线段的比。      （1）两条线段的比值总是正数；（2）求线段的比一定要用同一长度单位。2、在四条线段中，如果其中两条线段的比与另两条线段的比相等，那么这四条线段叫做成比例线段，简称比例线段。问题2：在中，DE是中位线，则DE与BC的比为多少？说一说其中成比例的线段有哪些？分析：根据三角形中位线定理，可知，所以，      因为DE为中位线，所以D为AB中点，E为AC中点，      所以，      所以线段DE、BC、AD、AB成比例，线段DE、BC、AE、AC成比例，          线段AD、AB、AE、AC成比例，线段BD、AB、EC、AC成比例，          线段AD、BD、AE、EC成比例，……板书：※如果是比例线段，则有，那么线段是比例外项，线段是比例内项。板书：3、比例线段的基本性质：如果，那么。解析：课前预习第1，2题。1、点B在线段AC上，BC=2AB，求下列各线段的比值：（1）AB:BC=      ；（2）AC:AB=      ；（3）BC:AC=      。2、下列各组线段成比例的是（      ）   A、1cm，3cm，2cm，4cm                 B、1cm，20cm，5cm，25cm     C、              D、4cm，8cm，6cm，12cm练习2、填空：（1）如果两条线段的长度分别为，那么2:5；（2）如果两地相距，那么在1:10000000的地图上表示这两地的点相距2.5cm；（3）已知，如果，则c:d；（4）若则的比例中项；（5）若线段则线段的比例中项线段。二、探索新知，获得感悟思考1：比例线段，且，除了上述性质以外，还有其它的性质吗？【说明】在预习的基础上请学生先来说一说，然后再进行证明。分析：。思考2：如何来证明上述性质的正确性？分析：（1）设，则有，          所以，          所以（同理可证明），。      （2）因为，所以，所以，则。等式性质             通分板书：4、比例的合比性质：如果，那么。5、比例的等比性质：如果，那么。解析：课前预习第3,4题。3、已知：，则        。4、已知，则     ，     ，     。思考3：如果，那么的值为多少？分析：因为，则，      所以。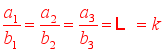板书：6、等比性质的推广：如果，                       那么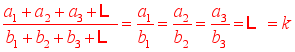。 三、例题选讲，训练提高例题1、已知：如图，。求证：（1）；（2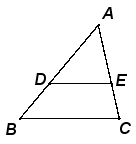）。【说明】本题是合比性质的具体运用，也是为学习三角形一边的平行线性质作铺垫。对证明思路的分析，要把握AB=AD+DB，AC=AE+EC这两个关系式。证明：（1）∵，∴，（合比性质）          ∴；     （2）∵，∴，（比例的基本性质）          ∴，（合比性质）∴。练习3、已知：如图，线段BD与CE相交于点A，。        求证：（1）；（2）。证明：（1）∵，∴，（比例的基本性质）          ∴，即，（合比性质）          ∴。（比例的基本性质）       （2）∵，∴，（比例的基本性质）即。例题2、已知：。求：的值。解：∵，∴，（合比性质）∴。例题3、已知：。求证：。证明1：∵，                              证明2：设        ∴，                                      则，（等比性质）        ∴，，（合比性质）     ∴。        ∴。（两个等式左右两边分别相除）例题4、已知：。求：的值。解：（1）若，∵，        ∴，则；   （2）若，则，        ∴。四、课堂小结，加深理解1、线段成比例的表达式是什么？2、比例的基本性质有哪些？3、什么是合比性质？什么是等比性质？它们有什么区别？五、回家作业，复习巩固1、复习24.2  比例线段（1），做好笔记整理；2、小卷子《24.1  放缩与相似形》签名；3、完成《数学练习册》：习题24.2（1）；4、完成《导学案》：24.2  比例线段（1）；5、预习《数学书》：P8-P10，24.2  比例线段（2）；6、完成《导学案》：24.2  比例线段（2），知识清单，课前预习。板书设计：     教学反思：