初中2.5 等腰三角形的轴对称性优秀课后练习题

这是一份初中2.5 等腰三角形的轴对称性优秀课后练习题，共8页。试卷主要包含了以下说法中，正确的命题是等内容，欢迎下载使用。
2021年苏科版数学八年级上册2.5《等腰三角形的轴对称性》同步练习卷一、选择题1.一个等腰三角形的两边长分别是3cm和7cm，则它的周长为(　　)A.17cm         B.15cm         C.13cm         D.13cm或17cm2.具备下列条件的△ABC中，不是直角三角形的是(   )A.∠A＋∠B=∠CB.∠A=2∠B=2∠CC.∠A∶∠B∶∠C=1∶2∶3D.∠A=∠B=3∠C3.如图,△ABC中,AB=5,AC=6,BC=4,边AB的垂直平分线交AC于点D,则△BDC周长是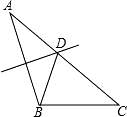（      ） A.8                          B.9                          C.10                             D.114.如图，在△ABC中，AB=AC，∠BAC=100°，AB的垂直平分线DE分别交AB、BC于点D、E，则∠BAE=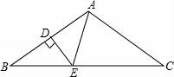（  ） A．80°              B．60°              C．50°              D．40°5.如果等腰三角形的一个底角为α，那么（       ）A.α不大于45°                B.0°＜α＜90°                C.α不大于90°               D.45°＜α＜90°6.如图，在△ABC中,AB=AC=4,∠ABC和∠ACB的平分线交于点E，过点E作MN∥BC分别交AB、AC于M、N,则△AMN的周长为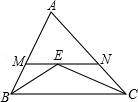（      ）   A.12           B.4              C.8                D.不确定7.下列关于等腰三角形的性质叙述错误的是（    ）A.等腰三角形的两底角相等B.等腰三角形的两边相等C.等腰三角形是轴对称图形D.等腰三角形底边上的高、底边上的中线、顶角的平分线互相重合8.等腰三角形的一个内角为70°，则另外两个内角的度数分别是（    ）A.55°，55°      B.70°，40°或70°，55°C.70°，40°        D.55°，55°或70°，40°9.如图，在△ABC中，∠A=36°，AB=AC，BD是△ABC的角平分线．若在边AB上截取BE=BC，连接DE，则图中等腰三角形共有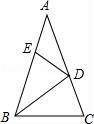（     ）A．2个                        B．3个                      C．4个                       D．5个10.以下说法中，正确的命题是（     ）（1）等腰三角形的一边长为4 cm，一边长为9 cm，则它的周长为17 cm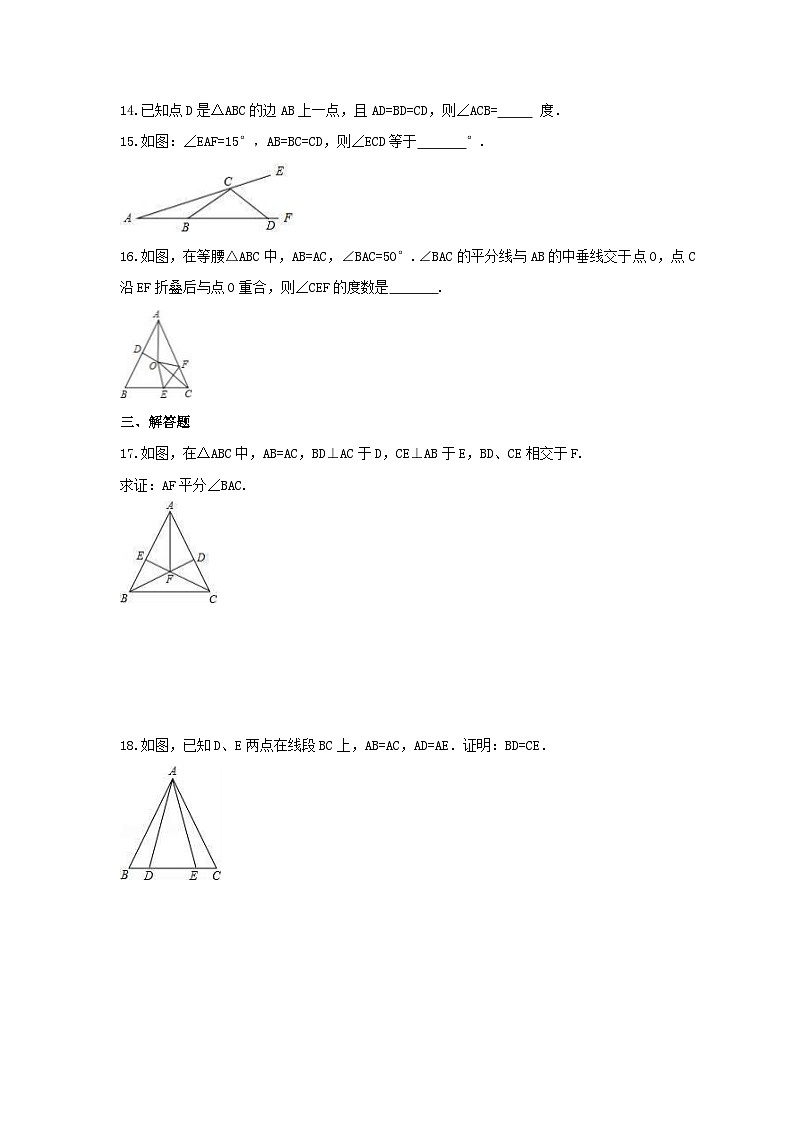或22 cm；（2）三角形的一个外角等于两个内角的和；（3）有两边和一角对应相等的两个三角形全等；（4）等边三角形是轴对称图形；（5）如果三角形的一个外角的平分线平行于三角形一边，那么这个三角形是等腰三角形．A．（1）（2）（3）  B．（1）（3）（5）  C．（2）（4）（5）  D．（4）（5）二、填空题11.等腰三角形中，已知两边的长分别是9和6，则周长为　   　.12.等腰三角形一腰上的高与底边的夹角为70°，则顶角的度数为　   　.13.如图，在△ABC中，∠C=35°，AB=AD，DE是AC的垂直平分线，则∠BAD=　　度.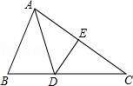14.已知点D是△ABC的边AB上一点，且AD=BD=CD，则∠ACB=      度．15.如图：∠EAF=15°，AB=BC=CD，则∠ECD等于　 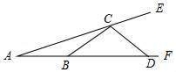  　°.16.如图，在等腰△ABC中，AB=AC，∠BAC=50°.∠BAC的平分线与AB的中垂线交于点O，点C沿EF折叠后与点O重合，则∠CEF的度数是　 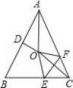  　.三、解答题17.如图，在△ABC中，AB=AC，BD⊥AC于D，CE⊥AB于E，BD、CE相交于F.求证：AF平分∠BAC. 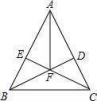   18.如图，已知D、E两点在线段BC上，AB=AC，AD=AE．证明：BD=CE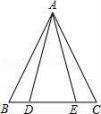．     19.如图，△ACB和△ADE均为等边三角形，点C、E、D在同一直线上，连接BD，试猜想线段CE、BD之间的数量关系，并说明理由. 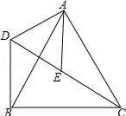    20.如图，在四边形ABCD中，AD∥BC，E为CD的中点，连接AE、BE，BE⊥AE，延长AE交BC的延长线于点F．求证：（1）FC=AD；（2）AB=BC+AD．
参考答案1.A.2.D.3.C4.D5.B6.C7.B8.D9.D10.D11.答案为：21或24.12.答案为140°.13.答案为：40.14.答案为：90．15.答案为：45.16.答案为：50°.17.证明：∵AB=AC(已知)，∴∠ABC=∠ACB(等边对等角).∵BD、CE分别是高，∴BD⊥AC，CE⊥AB(高的定义).∴∠CEB=∠BDC=90°.∴∠ECB=90°﹣∠ABC，∠DBC=90°﹣∠ACB.∴∠ECB=∠DBC(等量代换).∴FB=FC(等角对等边)，在△ABF和△ACF中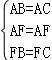，，∴△ABF≌△ACF(SSS)，∴∠BAF=∠CAF(全等三角形对应角相等)，∴AF平分∠BAC.18.证明：过A作AF⊥BC于F，∵AB=AC，AD=AE，AF⊥BC，∴BF=CF，DF=EF，∴BF﹣DF=CF﹣EF，∴BD=CE．19.解：CE=BD，理由：∵△ACB和△ADE均为等边三角形，∴AD=AE，AB=AC，∠DAE=∠BAC=60°，∴∠DAE﹣∠BAE=∠BAC﹣∠BAE，∴∠DAB=∠EAC.在△ADB和△AEC中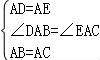，，∴△ADB≌△AEC（SAS），∴CE=BD.20.证明：（1）∵AD∥BC（已知），∴∠ADC=∠ECF（两直线平行，内错角相等），∵E是CD的中点（已知），∴DE=EC（中点的定义）．∵在△ADE与△FCE中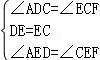，，∴△ADE≌△FCE（ASA），∴FC=AD（全等三角形的性质）．（2）∵△ADE≌△FCE，∴AE=EF，AD=CF（全等三角形的对应边相等），∴BE是线段AF的垂直平分线，∴AB=BF=BC+CF，∵AD=CF（已证），∴AB=BC+AD（等量代换）．