初中数学苏科版八年级上册6.1 函数优秀同步测试题

这是一份初中数学苏科版八年级上册6.1 函数优秀同步测试题，共8页。试卷主要包含了一次函数y=-1等内容，欢迎下载使用。
2021年苏科版数学八年级上册6.6《一次函数、一元一次方程和一元一次不等式》同步练习卷一、选择题1.已知函数y=2x﹣3的自变量x取值范围为1＜x＜5，则函数值的取值范围是（　　）                                          A.y＜﹣2，y＞2                       B.y＜﹣1，y＞7                       C.﹣2＜y＜2                  D.﹣1＜y＜7                            2.同一直角坐标系中，一次函数y1=k1x+b与正比例函数y2=k2x的图象如图,则满足y1≥y2的x取值范围是（     ）      A.x≤﹣2           B.x≥﹣2            C.x＜﹣2            D.x＞﹣23.一次函数y=﹣3x+b和y=kx+1的图象如图,其交点为P（3,4），则不等式（3+k）x≥b﹣1的解集在数轴上表示正确的是（      ）A．                     B．              C．                     D．4.已知一次函数y=kx+b的图象如图所示，则下列判断中不正确的是(       )A.方程kx+b=0的解是x=﹣3 B.k＞0，b＜0C.当x＜﹣3时，y＜0 D.y随x的增大而增大  5.如图，直线y=kx+b与x轴交于点(﹣4，0)，则y＞0时，x的取值范围是(     )A.x＞﹣4       B.x＞0      C.x＜﹣4        D.x＜06.如图，已知一次函数y=ax＋b的图像为直线l，则关于x的不等式ax＋b＜1的解集为( 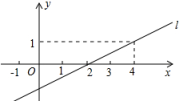   )A.x<0             B.x>0            C.x<1         D.x<27.一次函数y=kx＋b(k≠0)的图象如图所示，当y>0时，x的取值范围是(   )A.x＜0          B.x＞0            C.x＜-3            D.x＞-3 8.已知一次函数y=kx+b的图象如图，则关于x的不等式k(x-4)-2b≥0的解集为(     )A.x≥-2          B.x≤-2           C.x≤3            D.x≥39.一次函数y1=kx＋b与y2=x＋a的图象如图所示.则下列结论：①k<0；②a>0；③当x<3时，y1<y2，错误的个数是(      )A.0            B.1            C.2            D.3  10.一次函数y=-1.5x+3的图象如图所示,当-3<y<3时,x的取值范围是(      )A.x>4        B.0<x<2           C.0<x<4         D.2<x<4二、填空题11.当自变量x_______时，函数y=5x＋4的值大于0；当x_______时，函数的值小于0.12.如图，直线l是一次函数y=kx＋b的图像.观察图像，可知：(1)b=_______，k=_______；(2)当y>2时.x_______.13.如图，一次函数y=kx+b的图象与x轴、y轴分别相交于A、B两点，那么当y＜0时，自变量x的取值范围是　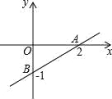      　．14.已知点A（0，m）和点B（1，n）都在函数y=﹣3x+b的图象上，则m       n．（在横线上填“＞”、“＜”或“=”）15.如图，直线：y=x+1与直线：y=mx+n相交于点P（a，2），则关于x的不等式=x+1≥=mx+n的解集为    ．
 16.若直线y=－2x+b经过点(3，5)，则关于x的不等式－2x+b<5的解集是     .  三、解答题17.已知函数y=－2x＋4.(1)画出它的图像；(2)当x为何值时，y<－4?(3)当y为何值时，－0.5≤x<1.5？     18.已知一次函数y=kx+b的图象如图所示(1)求k、b的值；(2)在平面直角坐标系内画出函数y=bx+k的图象；(3)利用(2)中你所画的图象，写出0＜x＜1时，y的取值范围.  19.已知一次函数y=-2x+4，完成下列问题：(1)求此函数图像与x轴、y轴的交点坐标；(2)画出此函数的图像；观察图像，当0≤y≤4时，x的取值范围是     ；(3)平移一次函数y=-2x+4的图像后经过点(-3，1)，求平移后的函数表达式.20.已知直线y=kx+b经过点A(5，0)，B(1，4).(1)求直线AB的解析式；(2)若直线y=2x﹣4与直线AB相交于点C，求点C的坐标；(3)根据图象，写出关于x的不等式2x﹣4＞kx+b的解集.
参考答案1.答案为：D．2.答案为：A3.答案为：B4.答案为：B5.答案为：A6.答案为：B7.答案为：C8.答案为：B9.答案为：C10.答案为：C.11.答案为：＞－0.8，＜－0.812.答案为：(1)3－k  (2)x<113.答案为：x＜2．14.答案为：＞．15.答案为：x≥1.16.答案为：3      17.解：(1)略；(2)当x>4时，y<－4(3)当1<y≤5时，－0.5≤x<1.5.18.解：(1)A(0，﹣2)，B(1，0).将A(0，﹣2)，B(1，0)两点代入y=kx+b中，得b=﹣2，k﹣2=0，k=2.(2)对于函数y=﹣2x+2，列表：x01y20图象如下：(3)由图象可得：当0＜x＜1时，y的取值范围为：0＜y＜2.19.解：(1)当x=0时y=4，∴函数y=-2x+4的图像与y轴的交点坐标为(0，4)；当y=0时，-2x+4=0，解得：x=2，∴函数y=-2x+4的图像与x轴的交点坐标(2，0).(2)图像略；观察图像，当0≤y≤4时，x的取值范围是0≤x≤2.(3)设平移后的函数表达式为y=-2x+b，将(-3，1)代入得：b+6=1，∴b=-5，∴y=-2x-5.答：平移后的直线函数表达式为：y=-2x-5.20.解：(1)∵直线y=kx+b经过点A(5，0)，B(1，4)，∴，解得，∴直线AB的解析式为：y=﹣x+5；(2)∵若直线y=2x﹣4与直线AB相交于点C，∴.解得，∴点C(3，2)；(3)根据图象可得x＞3.